Идеи решения пределов для чайника. Неопределённость, порядок роста функции

Определение предела последовательности

Хорошо, распишем последовательность

Нетрудно уловить, что подпоследовательность

бесконечно близко приближаются к числу –1, а члены с чётными номерами

– к «единице».

А может быть предела два? Но тогда почему у какой-нибудь последовательности их не может быть десять или двадцать? Так можно далеко зайти. В этой связи логично считать, что если у последовательности существует предел, то он единственный.

Примечание: у последовательности  нет предела, однако из неё можно выделить две подпоследовательности (см. выше), у каждой из которых существует свой предел.

Таким образом, высказанное выше определение оказывается несостоятельным. Да, оно работает для случаев вроде  (чем я не совсем корректно пользовался в упрощённых объяснениях практических примеров), но сейчас нам нужно отыскать строгое определение.

Попытка вторая: «предел последовательности – это число, к которому приближаются ВСЕ члены последовательности, за исключением, разве что их конечного количества». Вот это уже ближе к истине, но всё равно не совсем точно. Так, например, у последовательности

половина членов вовсе не приближается к нулю – они ему просто-напросто равны =) К слову, «мигалка»

вообще принимает два фиксированных значения.

Формулировку нетрудно уточнить, но тогда возникает другой вопрос: как записать определение в математических знаках? Научный мир долго бился над этой проблемой, пока ситуацию не разрешил известный маэстро, который, по существу, и оформил классический матанализ во всей его строгости. Коши предложил оперировать окрестностями, чем значительно продвинул теорию.

Рассмотрим некоторую точку

и её произвольную

Значение «эпсилон» всегда положительно, и, более того, мы вправе выбрать его самостоятельно. Предположим, что в данной окрестности находится множество членов (не обязательно все) некоторой последовательности

. Как записать тот факт, что, например десятый член попал в окрестность? Пусть он находится в правой её части. Тогда расстояние между точками

должно быть меньше «эпсилон»:

. Однако если «икс десятое» расположено левее точки «а», то разность будет отрицательна, и поэтому к ней нужно добавить знак модуля:

называется пределом последовательности, если для любой его окрестности

(заранее выбранной) существует натуральный номер

– ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерами

окажутся внутри окрестности:

Иными словами, какое бы малое значение «эпсилон» мы ни взяли, рано или поздно «бесконечный хвост» последовательности ПОЛНОСТЬЮ окажется в этой окрестности.

ПОЛНОСТЬЮ зайдёт в любую сколь угодно малую

. Таким образом, это значение является пределом последовательности

Следует отметить, что для последовательности

уже нельзя сказать «бесконечный хвост зайдёт» – члены с нечётными номерами по факту равны нулю и «никуда не заходят» =) Именно поэтому в определении использован глагол «окажутся». И, разумеется, члены такой последовательности, как

тоже «никуда не идут». Кстати, проверьте, будет ли число

Теперь покажем, что у последовательности

не существует предела. Рассмотрим, например, окрестность

. Совершенно понятно, что нет такого номера, после которого ВСЕ члены окажутся в данной окрестности – нечётные члены всегда будут «выскакивать» к «минус единице». По аналогичной причине не существует предела и в точке

Начинающим рекомендую 2-3 раза перечитать вышесказанное + параграф понятие предела последовательности предыдущего урока, где я объяснил то же самое, но без математических значков.

Закрепим материал практикой:

Доказать что предел последовательности

равен нулю. Указать номер

, после которого, все члены последовательности гарантированно окажутся внутри любой сколь угодно малой

Примечание: у многих последовательностей искомый натуральный номер  зависит от значения  –  отсюда и обозначение .

Решение: рассмотрим произвольную

и проверим, найдётся ли номер

– такой, что ВСЕ члены с бОльшими номерами

окажутся внутри этой окрестности:

Чтобы показать существование искомого номера

Так как при любом значении «эн»

, то знак модуля можно убрать:

Используем «школьные» действия с неравенствами, которые я повторял на уроках Линейные неравенства и Область определения функции. При этом важным обстоятельством является то, что «эпсилон» и «эн» положительны:

Поскольку слева речь идёт о натуральных номерах, а правая часть в общем случае дробна, то её нужно округлить:

Примечание: иногда для перестраховки справа добавляют единицу, но на самом деле это излишество. Условно говоря, если  и мы ослабим результат округлением в меньшую сторону , то ближайший подходящий номер («тройка») всё равно будет удовлетворять первоначальному неравенству.

А теперь смотрим на неравенство

и вспоминаем, что изначально мы рассматривали произвольную

Вывод: для любой сколько угодно малой

, такое, что для всех бОльших номеров

. Таким образом, число

К слову, из полученного результата

хорошо просматривается естественная закономерность: чем меньше

-окрестность –  тем больше номер

, после которого ВСЕ члены последовательности окажутся в данной окрестности. Но каким бы малым ни было «эпсилон» – внутри всегда будет «бесконечный хвост», а снаружи – пусть даже большое, однако конечное число членов.

Как впечатления? =) Согласен, что странновато. Но строго! Пожалуйста, перечитайте и осмыслите всё ещё раз.

Рассмотрим аналогичный пример и познакомимся с другими техническими приёмами:

Используя определение последовательности, доказать, что

Решение: по определению последовательности нужно доказать, что

и проверим, существует ли натуральный номер

– такой, что для всех бОльших номеров

Чтобы показать существование такого

, нужно выразить «эн» через «эпсилон». Упрощаем выражение под знаком модуля:

Модуль уничтожает знак «минус»:

Знаменатель положителен при любом «эн», следовательно, палки можно убрать:

Теперь надо бы извлечь квадратный корень, но загвоздка состоит в том, что при некоторых «эпсилон» правая часть будет отрицательной. Чтобы избежать этой неприятности усилим неравенство модулем:

Почему так можно сделать? Если, условно говоря, окажется, что

, то подавно будет выполнено и условие

. Модуль может только увеличить разыскиваемый номер

, и это нас тоже устроит! Грубо говоря, если подходит сотый, то подойдёт и двухсотый! В соответствии с определением, нужно показать сам факт существования номера (хоть какого-то), после которого все члены последовательности окажутся в

И округляем результат:

Вывод: т.к. значение «эпсилон» выбиралось произвольно, то для любой сколько угодно малой

Советую особо разобраться в усилении и ослаблении неравенств – это типичные и очень распространённые приёмы математического анализа. Единственное, нужно следить за корректностью того или иного действия. Так, например, неравенство

ни в коем случае нельзя ослаблять, вычитая, скажем, единицу:

Опять же условно: если номер

точно подойдёт, то предыдущий может уже и не подойти.

Следующий пример для самостоятельного решения:

Краткое решение и ответ в конце урока.

Если последовательность бесконечно велика, то определение предела формулируется похожим образом: точка

называется пределом последовательности, если для любого, сколь угодно большого числа

, такой, что для всех бОльших номеров

, будет выполнено неравенство

называют окрестностью точки «плюс бесконечность»:

Иными словами, какое бы большое значение

мы ни взяли, «бесконечный хвост» последовательности обязательно зайдёт в

И сокращённая запись:

запишите определение самостоятельно. Правильная версия в конце урока.

После того, как вы «набили» руку на практических примерах и разобрались с определением предела последовательности, можно обратиться к литературе по математическому анализу и/или своей тетрадке с лекциями. Рекомендую закачать 1-й том Бохана (попроще – для заочников) и Фихтенгольца (более подробно и обстоятельно). Из других авторов советую Пискунова, курс которого ориентирован на технические ВУЗы.

Попытайтесь добросовестно изучить теоремы, которые касаются предела последовательности, их доказательства, следствия. Поначалу теория может казаться «мутной», но это нормально – просто нужно привыкнуть. И многие даже войдут во вкус!

Порядок роста функции

В данном параграфе будут разобраны пределы с многочленами, многочленами под корнем, когда

Вычислим следующий предел:

На базовом уроке Пределы. Примеры решений я рекомендовал рассуждать не совсем корректным способом: сначала «икс» равно 10, потом, 100, затем 1000, миллион и т.д. до бесконечности. В чём изъян такого подхода? Построим данную последовательность:

Исходя из полученных результатов, складывается стойкое впечатление, что предел стремится к «минус бесконечности», но на поверку впечатление кардинально ошибочно:

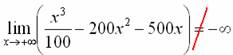
В этой связи необходимо знать теорию матана, а именно, некоторые выкладки о порядке роста функции.

обладает более высоким порядком роста, чем сумма

. Иными словами, при достаточно больших значениях «икс» слагаемое

«перетянет» на «плюс бесконечность» всё остальное:

При небольших значениях «икс» – да, сладкая парочка

перетягивает канат в сторону «минус бесконечности», что и привело нас к неверному первоначальному выводу. Но уже при

получается гигантское положительное число

Если сильно уменьшить первое слагаемое, то от этого ничего не изменится:

, будет лишь отсрочен тот момент, когда бравая дробь

«вытянет» весь предел на «плюс бесконечность». Не поможет и «усиление противовеса»:

.
Нулей можете приписать, сколько хотите (без шуток). Удивительная наука математический анализ – способна низвести любого монстра до мелочи пузатой.

Таким образом, кубическая функция имеет более высокий порядок роста, чем:

– квадратичная функция;
– линейная функция;
– функция-константа;
– сумма квадратичной функции, линейной функции и константы (в любых комбинациях).

На простейшем примере поясню геометрический смысл вышесказанного. Представьте графики линейной

функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола

взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.

Аналогичное правило можно сформулировать для любой степени:

Степенная функция данной степени растёт быстрее, чем любая степенная функция более низкой степени. И быстрее, чем сумма любого количества степенных функций более низкой степени.

Значение данного предела зависит только от слагаемого

. Всё остальное МЫСЛЕННО отбрасываем:

, и теперь ясно как день, что предел стремится к «минус бесконечности»:

То есть, слагаемое

могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ.

Сравнение бесконечно больших функций

На первом уроке мы вычислили три предела с неопределённостью

В перечисленных примерах используется стандартный приём деления числителя и знаменателя на «икс» в старшей степени и всё расписывается подробно. Но правильный ответ легко выяснить ещё до решения!

В первом примере

в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:

В таких случаях говорят, что функции числителя и знаменателя обладают одинаковым порядком роста. Или короче – числитель и знаменатель одного порядка роста. Действительно, в данном пределе и вверху, и внизу находятся квадратичные функции. Мир, равенство, братство.

Во втором примере

аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:

Здесь знаменатель более высокого порядка, чем числитель. Функция-многочлен 4-й степени растёт быстрее кубической функции и «перетягивает» предел на ноль.

И, наконец, в пределе

карлики тоже идут лесом:

А в этом примере всё наоборот – числитель более высокого порядка, чем знаменатель. Квадратичная функция растёт быстрее линейной и «перетягивает» предел на «плюс бесконечность».

Сделаем краткую теоретическую выжимку. Рассмотрим две произвольные функции

– ненулевая константа, то функции имеют одинаковый порядок роста. Если

, то функция

более высокого порядка роста, чем

! Примечание: при  суть выкладок не меняется.

В наличии неопределённость

Почему бы сразу не узнать ответ? В числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:

Разделим числитель и знаменатель на

В действительности пару шагов можно пропустить, просто я подробно расписал, как в знаменателе под корень вносится

Это пример для самостоятельного решения. Постарайтесь провести рассуждения по образцу первого примера. Также заметьте, что здесь неопределённость

Во избежание недочёта, всегда анализируйте, какая неопределённость получается в пределах рассматриваемого вида. Помимо неопределённости

может встретиться неопределённость

. Во всех четырёх случаях числитель и знаменатель необходимо разделить на «икс» в старшей степени.

Слишком трудный предел? Лёгкий испуг от хлопушки. Главное, грамотно управиться с радикалами.

Проведём предварительный анализ:

Сначала выясним старшую степень числителя. Там сумма двух корней. Под корнем

отбросим младшее слагаемое:

и уберём константу:

отбросим все младшие слагаемые:

, значит, старшая степень числителя:

Разбираемся с нижним этажом. Под корнем

. У многочлена

старшая степень равна двум.

, значит, старшая степень знаменателя:

.
Кстати, заметьте, что корень

Сравниваем старшие степени:

Оформляем решение, я распишу его максимально подробно:

Разделим числитель и знаменатель на «икс» в старшей степени:

Действия в числителе прозрачны, закомментирую знаменатель. У дроби

«разнокалиберные» корни, и квадратный корень

необходимо «подогнать» под кубический корень

. Составим и решим уравнение:

. Таким образом:

Ну и на всякий случай напоминаю формулу

, по которой выполняется деление:

Другие члены знаменателя:

Правила действий с корнями можно найти на странице Математические формулы и таблицы в методичке Горячие формулы школьного курса математики. Также на действиях с радикалами я подробно останавливался при нахождении производных.

Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость

более высокого порядка роста, чем корень

Если «икс» стремится к «минус бесконечности»

Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых

. Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.

Рассмотрим 4 фишки, которые потребуются для решения практических заданий:

1) Вычислим предел

Значение предела зависит только от слагаемого

, поскольку оно обладает самым высоким порядком роста. Если

, то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени, в данном случае – в четвёртой, равно «плюс бесконечности»:

. Константа («двойка») положительна, поэтому:

2) Вычислим предел

Здесь старшая степень опять чётная, поэтому:

. Но перед

расположился «минус» (отрицательная константа –1), следовательно:

3) Вычислим предел

. Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае:

.
Константа («четвёрка») положительна, значит:

4) Вычислим предел

Первый парень на деревне

снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит:

Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость

. Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

А сейчас, пожалуй, самый тонкий из случаев:

Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость

. Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:

Проанализируем бесконечно малые слагаемые знаменателя:

, то слагаемые с чётными степенями

будут стремиться к бесконечно малым положительным числам (обозначаются через

), а слагаемые с нечётными степенями

будут стремиться к бесконечно малым отрицательным числам (обозначаются через

Теперь зададимся вопросом, какое из этих четырёх слагаемых

будет стремиться к нулю (неважно с каким знаком) медленнее всего? Вспомним наивный приём: сначала «икс» равно –10, потом –100, затем –1000 и т.д. Медленнее всего к нулю будет приближаться слагаемое

. Образно говоря, это самый «жирный» ноль, который «поглощает» все остальные нули. По этой причине на завершающем этапе и появилась запись

Следует отметить, что знаки бесконечно малых слагаемых числителя нас не интересуют, поскольку там нарисовалась осязаемая добротная единичка. Поэтому в числителе я поставил «просто нули». К слову, знаки при нулях не имеют значения и во всех примерах, где в пределе получается конечное число (Примеры №№5,6).

Без измен, на то он и математический анализ, чтобы анализировать =)

Впрочем, о бесконечно малых функциях позже, а то вы нажмёте маленький крестик справа вверху =)

Рекомендую хорошо осмыслить информацию первой части урока, и по возможности сделать перерыв.

Устранение неопределённости «единица в степени бесконечность»

Данную неопределённость «обслуживает» второй замечательный предел, и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.

Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?

На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):

Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.

Выделим существенные моменты формулы:

1) Речь идёт только о неопределённости  и никакой другой.

2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или

С помощью данной формулы можно решить все примеры урока Замечательные пределы, которые относятся ко 2-му замечательному пределу. Например, вычислим предел

, и по формуле

Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-й замечательный предел.

Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:

На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость

Чтобы не таскать за собой букву «е» и не мельчить, показатель

В данном случае:

С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим  константы и проводим сокращения, избавляясь от неопределённости 0:0.

Обещанный подарок с разностью логарифмов и неопределённостью

Сначала полное решение, потом комменты:

(1)-(2) На первых двух шагах используем формулы

. У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».

(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.

(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы, преобразуем неопределённость

(6) Используем формулу

(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма:

. Минус перед дробью вносим в знаменатель:

(8) Без комментариев =)

Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.

Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде

свести решение к случаю

В заключение рассмотрим пределы-«фальшивки».

Вернёмся к неопределённости

. Данную неопределённость далеко не всегда можно свести к неопределённости

и воспользоваться 2-м замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции. На пример:

Отвлечёмся от показателя и вычислим предел основания:

В пределе получена единица, значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны. На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости

Аналогичных пределов можно придумать очень много:

Дроби данных примеров объединяет вышеуказанная особенность:

.  В других случаях при неопределённости

Как ни старайся, а неопределённость

не удастся преобразовать в неопределённость

Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты:

Таким образом, 2-й замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ.

! Примечание: не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .

Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменатель основания разделить на «икс» в старшей степени (невзирая на показатель):

Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:

Это короткие примеры для самостоятельного изучения

Иногда неопределённости может не быть вообще:

Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!

Завершая тотальное разоблачение пределов, я хочу поздравить всех посетителей сайта с новым 2013 годом! С подарком я успел, и постинг данной статьи осуществлен 31 декабря 2012 года. Вы спросите, а как же моя личная подготовка к празднику? Давно готов =) На протяжении многих лет я занимаюсь стратегическим планированием – чтобы не толкаться в очередях до и не пересекаться с краснокожими после =)

Решения и ответы:

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys

Предел последовательности и предел функции по Коши

Сегодня на уроке мы разберём строгое определение последовательности и строгое определение предела функции, а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна. И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется 😉 Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!) о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций, в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей, на котором я фактически уже сформулировал строгое определение.

На начальном этапе не рекомендую особо заглядывать в учебник по математическому анализу, да и в собственные записи тоже. Хотя давайте немного причастимся:

Какие значки помимо знаков неравенств и модуля вы знаете?

Из курса алгебры нам известны следующие обозначения:

– квантор всеобщности обозначает– «для любого», «для всех», «для каждого», то есть запись

– квантор существования,

– существует значение

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что», в нашем случае, очевидно, речь идёт о номере

– для всех «эн», бОльших чем

– знак модуля означает расстояние, т.е. эта запись сообщает нам о том, что расстояние между значениями

А теперь попытайтесь прочитать строку

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

• предел обозначается значком lim;
• затем справа дописывается сама функция, например:

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

Строгое определение предела функции

Начнём с того же самого – как сформулировать данное понятие? Словесное определение предела функции

формулируется значительно проще: «число

является пределом функции

, если при «икс», стремящемся к

(и слева, и справа), соответствующие значения функции стремятся к

» (см. чертёж). Всё вроде бы нормально, но слова словами, смысл смыслом, значок

определена на некотором промежутке

за исключением, возможно, точки

. В учебной литературе общепринято считают, что функция там не определена:

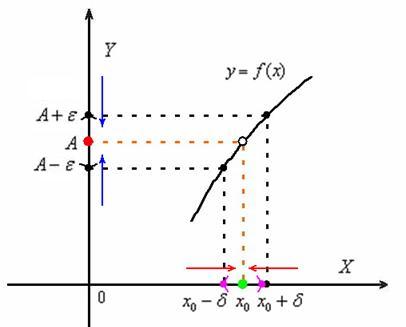
Такой выбор подчёркивает суть предела функции: «икс» бесконечно близко приближается к

, и соответствующие значения функции – бесконечно близко к

.
Иными словами, понятие предела подразумевает не «точный заход» в точки, а именно бесконечно близкое приближение, при этом не важно – определена ли функция

Первое определение предела функции, что неудивительно, формулируется с помощью двух последовательностей. Во-первых, понятия родственные, и, во-вторых, пределы функций обычно изучают после пределов последовательностей.

точек (на чертеже отсутствуют), принадлежащих промежутку

и отличных от

, которая сходится к

. Тогда соответствующие значения функции

Предел функции по Гейне: число

называется пределом функции

, если для любой последовательности точек

), которая сходится к точке

, соответствующая последовательность значений функции

-окрестность, которая соответствует заданной

-окрестности (мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз). Обратите внимание, что значение

выбираетсяпо длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую»

можно даже уменьшить, поскольку в нижеследующем определении важен сам факт существования этой окрестности. И, аналогично, запись

означает, что некоторое значение

Предел функции по Коши: число

, если для любойзаранее выбранной окрестности

(сколь угодно малой), существует

, ТАКАЯ, что: КАК ТОЛЬКО значения

) входят в данную окрестность:

(красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в

Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

В чём суть определения? Образно говоря, бесконечно уменьшая

Согласно соответствующей теореме математического анализа, определения по Гейне и по Коши эквивалентны, однако наиболее известен второй вариант (ещё бы!), который также называют «предел на языке

определение предела, доказать, что

Решение: функция определена на всей числовой прямой кроме точки

. Используя определение

, докажем существование предела в данной точке.

Примечание: величина «дельта»-окрестности зависит от «эпсилон», отсюда и обозначение

-окрестность. Задача состоит в том, чтобы по этому значению

проверить, существует ли

-окрестность, ТАКАЯ, что из неравенства

, преобразуем последнее неравенство:

(разложили квадратный трёхчлен)

Конечно, существует, например,

. В этом случае из неравенства

(формально оно же само). Следует отметить, что  в качестве примера можно привести и любую меньшую «дельта»-окрестность, например,

, поскольку из неравенства

тем более следует, что

(из того, что «в кармане меньше 50 рублей» следует то, что «в кармане меньше 100 рублей»). Однако в качестве стандартного примера окрестности практически всегда берут «пограничное»  значение, в данном примере

Вывод: для любой сколько угодно малой

, такая, что из неравенства

по определению предела функции. Ч.т.д.

Небольшое задание для самостоятельного решения.

Слишком просто? А вы попробуйте грамотно оформить, и, самое главное, ПОНЯТЬ, ход решения 😉

Следует отметить, что рассмотренные задачи не дают нам каких-то способов решения пределов, они позволяют лишь доказать либо опровергнуть существование некоторых из них.

Определение бесконечного предела, в частности предела

, тоже формулируется двумя способами. Приведу наиболее популярный вариант. Пусть функция

определена на промежутке

, который содержит сколь угодно большие значения «икс». Предел функции

равен «плюс бесконечности» при

, если для любого сколь угодно большого числа

(заранее заданного) найдётся окрестность

, такая, что: КАК ТОЛЬКО значения аргумента войдут в данную окрестность:

(красная стрелка), ТАК СРАЗУ соответствующие значения функции зайдут в

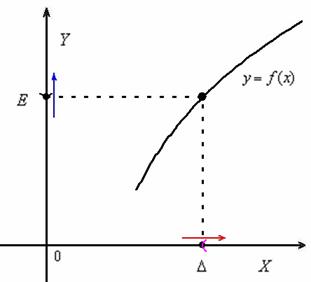
Определения следующих двух пределов предлагаю сформулировать самостоятельно:

Изобразите на чертеже принципиальную картину, прорисуйте окрестности и постарайтесь корректно записать определения. Для обозначения закрытых окрестностей используйте буквы

, для открытых к бесконечности – буквы

. Ответы в конце урока.

Случаи «минус бесконечности» и обобщённый случай легко отыскать в соответствующей литературе.

Ни в коем случае не расстраивайтесь, если дела «пойдут не очень», в конце концов, тут нужно принять во внимание, что учиться на «технаря» вообще непросто: что-то даётся легче, что-то труднее, а с чем-то может и помучиться придётся. Лично у меня некоторые разделы математики шли лучше, некоторые хуже, а программирование вообще переносилось с трудом (уж не знаю, почему). Нельзя идеально знать и любить всё.

Оглядываясь в прошлое, с улыбкой вспоминаю свои первый месяцы учёбы – тогда математический анализ показался мне самой трудной дисциплиной, и я с перепуга выучил ВЕСЬ материал 1-го семестра, даже сказать точнее не выучил, а почти во всём разобрался, чего и всем желаю!

Надеюсь, данная статья была полезна, а может, и послужила ключом к предмету!

Пример 3: Решение: докажем, что

. Для этого рассмотрим произвольную

и проверим, найдётся ли натуральный номер

Преобразуем неравенство:

Для всех «эн»:

: т.к. «эпсилон» выбиралось произвольно, то для любой сколько угодно малой

Пример 5: Решение: функция определена на всей числовой прямой. Используя определение , докажем существование предела в точке .
Рассмотрим произвольную -окрестность и проверим, найдётся ли -окрестность, такая что из неравенства
 следует .

Преобразуем неравенство с «эпсилон»:

В качестве искомой окрестности выбираем .
Вывод: для любой сколь угодно малой -окрестности точки  нашлось значение , такое, что , следовательно,  по определению. Ч.т.д.

Формулировки пределов:
, если
, если

Метод замены переменной в пределе

Весьма ходовой приём решения. Метод замены переменной применяют чаще всего для того, чтобы свести решение к первому замечательному пределу, намного реже – к другому замечательному пределу. Рассмотрим пару типовых образцов:

В пределе находится арктангенс, от которого хорошо бы избавиться. Логично и очень удобно превратить «арк» в одну единственную букву. Проведём замену переменной:

Теперь в пределе нужно выразить всё остальное через «тэ».

Во-первых, выясним, куда будет стремиться новая переменная «тэ»:
Если

, иными словами, новоиспеченная переменная тоже будет стремиться к нулю:

Осталось в знаменателе выразить «икс» через «тэ». Для этого на обе части равенства

В правой части две взаимно обратные функции уничтожаются:

Взмахи волшебной палочки закончены, остальное просто:

Используемые формулы и приёмы решения завершающего этапа очень подробно разобраны в первой части урока Замечательные пределы.

Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.

Ещё пара занятных примеров на тему замены переменной:

При подстановке единицы в предел получается неопределённость

. Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле

. Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице. Таким образом, мы сразу избавляемся от множителя

Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены

(1) Проводим подстановку

(2) Раскрываем скобки под косинусом.

(3) Используем формулу приведения

(4) Чтобы организовать первый замечательный предел

, искусственно домножаем числитель на

и обратное число

Задание для самостоятельного решения:

Полное решение и ответ в конце урока.

Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения, приходится использовать самые разные тригонометрические формулы, а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)

В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:

Пределы функций. Примеры решений

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям матана и заложил его основы. Надо сказать, этот уважаемый математик снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причём одна теорема убойнее другой. В этой связи мы пока не будем рассматривать определение предела по Коши, а попытаемся сделать две вещи:

1. Понять, что такое предел.
2. Научиться решать основные типы пределов.

Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.

Итак, что же такое предел?

Любой предел состоит из трех частей:

1) Всем известного значка предела

.
2) Записи под значком предела, в данном случае

. Запись читается «икс стремится к единице». Чаще всего – именно

, хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность (

).
3) Функции под знаком предела, в данном случае

читается так: «предел функции

при икс стремящемся к единице».

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Разбираемся, что такое

? Это тот случай, когда

неограниченно возрастает, то есть: сначала

и так далее до бесконечности.

Итак: если , то функция  стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию   бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать

до бесконечности и смотрим на поведение функции:

неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, попробуйте построить последовательность

! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом:

, то все равно

, так как рано или поздно «икс» начнёт принимать такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , ,  и т.д.

Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с интересными случаями, когда предела функции вообще не существует!

На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов. Кстати, по этой теме есть интенсивный курс в pdf-формате, который особенно полезен, если у Вас ОЧЕНЬ мало времени на подготовку. Но материалы сайта, разумеется, не хуже:

Пределы с неопределенностью вида  и метод их решения

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида

. Можно было бы подумать, что

, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим

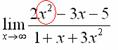
Теперь смотрим на знаменатель и тоже находим

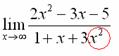
Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на  в старшей степени.

Вот оно как, ответ

, а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

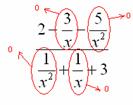
Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Снова в числителе и знаменателе находим

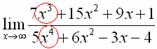
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности

делим числитель и знаменатель на

Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 (

можно записать как

)
Для раскрытия неопределенности

Таким образом, при раскрытии неопределенности вида

у нас может получиться конечное число, ноль или бесконечность.

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Сначала попробуем подставить -1 в дробь:

В данном случае получена так называемая неопределенность

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида

, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него:

В случае если дискриминант большой, например 361,  используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.

! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.

Далее находим корни:

Всё. Числитель на множители разложен.

Очевидно, что можно сократить на

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на множители.

Сначала «чистовой» вариант решения

Разложим числитель и знаменатель на множители.

Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.

Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.

Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.

! Важно
В ходе решения фрагмент типа  встречается очень часто. Сокращать такую дробь нельзя. Сначала нужно поменять знак у числителя или у знаменателя (вынести -1 за скобки).
, то есть появляется знак «минус», который при вычислении предела учитывается и терять его совсем не нужно.

Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.

Получена неопределенность вида

, которую нужно устранять.

Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.

Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности

Вспоминаем нашу нетленную формулу разности квадратов:

И смотрим на наш предел:

Что можно сказать?

у нас в числителе уже есть. Теперь для применения формулы осталось организовать

(которое и называется сопряженным выражением).

Умножаем числитель на сопряженное выражение:

Обратите внимание, что под корнями при этой операции мы ничего не трогаем.

мы организовали, но выражение-то под знаком предела изменилось! А для того, чтобы оно не менялось, нужно его разделить на то же самое, т.е. на

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.

Умножили. Теперь самое время применить вверху формулу

Число, как уже отмечалось ранее, лучше вынести за значок предела.

Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:

Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:

Умножим числитель и знаменатель на сопряженное выражение.

Сначала попробуйте решить его самостоятельно.

Окончательное решение примера может выглядеть так:

Разложим числитель на множители:

Спасибо за внимание.

Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы. После освоения двух базовых уроков, рекомендую изучить статью Методы решения пределов, материалы которой позволят выйти на «твёрдую четвёрку»!