Реферат – комплексные числа и их свойства
6.Комплексные числа и координатная плоскость.
ПрипереходекгеометрическоймоделимножестваСкомплексныхчисел
требуется,какминимум,ещёодноизмерение:ведьвсеточкипрямойуже
«заняты»действительнымичислами.Оказывается,геометрическоймоделью
множества C являетсякоординатнаяплоскость.Каждомукомплексномучислу
можноестественнымобразомпоставитьвсоответствиеточкукоординатной
плоскости.Тогдалюбомукомплексномучислусоответствуетединственная
точка на координатной плоскости, и наоборот, каждая точка плоскости
является «изображением» единственного комплексного числа.
В случаес комплексными числами,в соответствие счисловой прямой,
отождествлениесточкамикоординатнойплоскости.Например,фраза:«число
z
1
лежитвпервойкоординатнойчетверти»–простоозначает,чтои
действительнаяимнимаячастикомплексногочисла
положительны.Слова«z2лежитнаосиординат»являютсяпереводомна
геометрический языктого факта,что числоz
2
чисто мнимое, а «…комплексное
число z
3
расположенывышебиссектрисы1и3координатныхчетвертей…»–
показывают,чтомыимеемделоскомплекснымчисло,укоторого
мнимаячастьбольшедействительнойчасти.
Иногдаприведенныеправиладлясложения,вычитаниякомплексныхчисели
умножениякомплексныхчиселнадействительныечисламобъединяюттаким
образом:вомножествокомплексныхчиселоперациисложения,вычитанияи
умножениявычитанияиумножениянадействительныечислапроизводятся
покоординатно.Подчеркнемчтосамаэтаформулировкапредполагает
операцииуженессамимикомплекснымичислами,асихгеометрическими,
векторными представлениями.
у
х
0
Z
3
Z
1
Z
2
y=x
§
= 0, т.е. х
2
|х| = 0. Но это возможно только при х = 0 (ведь х – действительное число.)
Итак, данное уравнение имеет три корня: z
1
= 0, z
2
= i, z
3
= -i.
7)Задачи,связанныесрешениемразличныхуравнений,
содержащих комплексные переменные.
МножествоЕсостоитизвсехкомплексныхчиселz,таких,что,
.Найдитевсетакиечислаz
о
,чтодлялюбыхz
1
иz
2
изЕ
Решение.
9х
2
9у
2
= (х 4)
2
(у-8)
2
9х
2
– х
2
– 8х – 16 9у
2
– у
2
16у – 64 =0
8х
2
– 8х – 16 8у
2
16у – 64 =0
х
2
– х – 2 у
2
2у – 8 =0
(х – 0,5)
2
(у 1)
2
= 11,25
Окружность с центром (0,5; –1)
Ответ: z
о
= 0,5 – i
8). Среди всех комплексных чисел z, таких, что, есть ровно одно
число, аргумент которого равен . Найдите это число.
Решение.
Т.к.аргументравен,тоегодействительнаяимнимаячасти
противоположны.Причёмдействительнаячастьсознаком“-”,амнимая“ ”,
тогда z = – x xi, x > 0
(2 – x)
2
(x – 3)
2
= a
2
4 – 4x x
2
x
2
– 6x 9 = a
2
2(x – 2,5)
2
– 12,5 13 = а
2
2(x – 2,5)
2
= а
2
– 0,5
(x – 2,5)
2
= 0,5(а
2
– 0,5)
Поусловиюровноодночислоудовлетворяетэтомусоотношению.Значит,
уравнениедолжноиметькратныйкорень,чтовозможнотольколишьприa
(а – число неотрицательное).
x = 5/2a = 2,5
Ответ: z = – 2,5 2,5i
Реферат: комплексные числа –
Комплексные числа
[S1]ИСТОРИЧЕСКАЯ СПРАВКА
Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный корень.
1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА
Решение многих задач математики, физики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.
Так для решимости уравнений вида X A=B положительных чисел недостаточно. Например, уравнение X 5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A·X B=0 (A![]() 0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2
0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2
=2, X3
=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X2
1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.
Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнение X2
1=0 имеет корень. Обозначим этот корень буквой i
Таким образом, i
– это комплексное число, такое, что i2
= –1.
Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A B·i
можно считать записью комплексного числа в общем виде. Название “комплексное” происходит от слова “составное”: по виду выражения A B·i.
Комплексными числами
называют выражения вида A B·i
, где A и B –действительные числа, а i
– некоторый символ, такой что i2
= –1, и обозначают буквой Z.
Число A называется действительной частью комплексного числа A B·i,
а число B – его мнимой частью. Число i
называется мнимой единицей.
Например, действительная часть комплексного числа 2 3·i
равна 2, а мнимая равна 3.
Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.
Два комплексных числа A B·i
и C D·i
называются равными
тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.
2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА
Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A B·i
можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A B·i
изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат. Такая координатная плоскость называется комплексной плоскостью
. Ось абсцисс называется действительной осью
, т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью
– на ней лежат точки, соответствующие мнимым комплексным числам.
Не менее важной и удобной является интерпретация комплексного числа A B·i
как вектора, т.е. вектора с началом в точке
O(0;0) и с концом в точке М(A;B) (рисунок 2).
Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.
3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
Пусть дано комплексное число Z=A B·i
. Сопряженным
с Z
называется комплексное число A – B·i
, которое обозначается ![]() , т.е.
, т.е.
![]() =
=![]() =A – B·i
=A – B·i
.
Отметим, что ![]() = A B·i
= A B·i
, поэтому для любого комплексного числа Z имеет место равенство ![]() =Z.
=Z.
Модулем
комплексного числа Z=A B·i
называется число![]() и обозначается
и обозначается ![]() , т.е.
, т.е.
![]() =
=![]() =
=![]() (1)
(1)
Из формулы (1) следует, что ![]() для любого комплексного числа Z, причем
для любого комплексного числа Z, причем ![]() =0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
=0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:
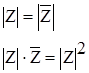
4.СЛОЖЕНИЕ И УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Суммой
двух комплексных чисел A B·i
и C D·i
называется комплексное число (A C) (
B D)·i
, т.е. (A B·i) (C D·i)=(A C) (B D)·i
Произведением
двух комплексных чисел A B·i
и C D·i
называется комплексное число (A·C – B·D) (A·D B·C) ·i
, т.е.
(A B·i)·(C D·i)=(A·C – B·D) (A·D B·C)·i
Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i2
= –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:
Переместительное свойство:
Z1
Z2
=Z2
Z1
, Z1
·Z2
=Z2
·Z1
Сочетательное свойство:
(Z1
Z2
) Z3
=Z1
(Z2
Z3
), (Z1
·Z2
)·Z3
=Z1
·(Z2
·Z3
)
Распределительное свойство:
Z1
·(Z2
Z3
)=Z1
·Z2
Z1
·Z3
Геометрическое изображение суммы комплексных чисел
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:
Сумма двух векторов с координатами (A1
;B1
) и (A2
;B2
) есть вектор с координатами (A1
A2
;B1
B2
). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1
и Z2
нужно сложить векторы, соответствующие комплексным числам Z1
и Z2
.
Пример 1:
Найти сумму и произведение комплексных чисел Z1
=2 – 3×i
и
1 Способ:
Z2
= –7 8×i
.
Z1
Z2
= 2 – 7 (–3 8)×i = –
5 5×i
Z1
×Z2
= (2 – 3×i
)×(–7 8×i
) = –14 16×i
21×i
24 = 10 37×i
2 Способ:
5.ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чисел Z1
и Z2
существует, и притом только одно, число Z, такое, что:
Z Z2
=Z1
Если к обеим частям равенства прибавить (–Z2
) противоположное числу Z2
:
Z Z2
(–Z2
)=Z1
(–Z2
), откуда
Z = Z1
– Z2
Число Z=Z1
Z2
называют разностью чисел
Z1
и Z2
.
Деление вводится как операция, обратная умножению:
Z×Z2
=Z1
Разделив обе части на Z2
получим:
Z=![]()
Из этого уравнения видно, что Z2![]() 0
0
Геометрическое изображение разности комплексных чисел
Разности Z2
– Z1
комплексных чисел Z1
и Z2
, соответствует разность векторов, соответствующих числам Z1
и Z2
. Модуль ![]() разности двух комплексных чисел Z2
разности двух комплексных чисел Z2
и Z1
по определению модуля есть длина вектора Z2
– Z1
. Построим этот вектор, как сумму векторов Z2
и (–Z1
) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с успехом использовать простые геометрические факты.
Пример 2:
Даны комплексные числа Z1
= 4 5·i
и Z2
= 3 4·i
. Найти разность Z2
– Z1
и частное ![]()
Z2
– Z1
= (3 4·i
) – (4 5·i
) = –1 – i
![]() =
=![]() =
=![]()
6.ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Запись комплексного числа Z в виде A B·i
называется алгебраической формой
комплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.
Рассмотрим тригонометрическую форму
записи комплексного числа. Действительная и мнимая части комплексного числа Z=A B·i
выражаются через его модуль ![]() = r и аргумент j следующим образом:
= r и аргумент j следующим образом:
A= r·cosj ; B= r·sinj.
Число Z можно записать так:
Z= r·cosj i
·![]() ·sinj = r·(cosj i
·sinj = r·(cosj i
·sinj)
Z = r·(cosj i
·sinj) (2)
Эта запись называется тригонометрической формой комплексного числа.
r =![]() – модуль комплексного числа.
– модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z![]() 0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случае число задается только своим модулем.
Как уже говорилось выше ![]() = r =
= r =![]() , равенство (2) можно записать в виде
, равенство (2) можно записать в виде
A B·i
=![]() ·cosj i
·cosj i
·![]() ·sinj,
·sinj,
откуда приравнивая действительные и мнимые части, получим:
cosj
= , sinj
, sinj
= (3)
(3)
Если sinj
поделить на cosj
получим:
tgj
=![]()
(4)
Эту формулу удобней использовать для нахождения аргумента j
, чем формулы (3). Однако не все значения j, удовлетворяющие равенству (4), являются аргументами числа A B·i.
Поэтому при нахождении аргумента нужно учесть, в какой четверти расположена точка A B·i.
7.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА КОМПЛЕКСНОГО ЧИСЛА
С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.
Пусть Z1
= r1
·(cosj1 i·sinj1),
Z2
= r2
·(cosj2 i·sinj2).
Тогда:
Z1
Z2
= r1
·r2[cosj1·cosj2 – sinj1·sinj2 i·( sinj1·cosj2 cosj1·sinj2)]=
=
r1
·r2[cos(j1 j2) i·sin(j1 j2)]
.
Таким образом, произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:
Z1
Z2
= r1
·r2[cos(j1 j2) i·sin(j1 j2)]
(5)
Из формулы (5) следует, чтопри умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Если Z1
=Z2
то получим:
Z2
=[r·(cosj i·sinj)]2
=
r2
·(cos2j i·sin2j)
Z3
=Z2
·Z= r2
·(cos2j i·sin2j)·r·(cosj i·sinj)=
=
r3
·(cos3j i·sin3j)
Вообще для любого комплексного числа Z
= r·( cosj i·sinj)![]() 0
0
и любого натурального числа n справедлива формула:
Zn=[ r·(cosj i·sinj)]n
= rn·( cosnj i·sinnj),
(6)
которую называют формулой Муавра.
Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:
![]()
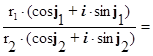
![]() [ cos(j1 – j2) i·sin(j1 – j2)].
[ cos(j1 – j2) i·sin(j1 – j2)].
(7)
 =
=  = cos(–j2) i·sin(–j2)
= cos(–j2) i·sin(–j2)
Используя формулу 5
 (cosj1 i·sinj1)×( cos(–j2) i·sin(–j2)) =
(cosj1 i·sinj1)×( cos(–j2) i·sin(–j2)) =
cos(j1 – j2) i·sin(j1 – j2).
Пример 3:
Z3
= –8
Число –8 запишем в тригонометрической форме
8 = 8·( cos(p 2pk) i
·sin(p 2pk)), kÎZ
Пусть Z = r×(cosj i
×sinj), тогда данное уравнение запишется в виде:
r3
×(cos3j i
×sin3j) = 8·( cos(p 2pk) i
·sin(p 2pk)), kÎZ
Тогда 3j =p 2pk, kÎZ
j
=![]() ,
,
kÎZ
r3
= 8
r = 2
Следовательно:
Z = 2·( cos(![]() ) i
) i
·sin(![]() )), kÎZ
)), kÎZ
k = 0,1,2…
k = 0
Z1
= 2·( cos![]() i
i
·sin![]() ) = 2·(
) = 2·(![]() i
i
) = 1 ![]() ×i
×i
k = 1
Z2
= 2·( cos(![]()
![]() ) i
) i
·sin(![]()
![]() )) = 2·( cosp i
)) = 2·( cosp i
·sinp) = –2
k = 2
Z3
= 2·( cos(![]()
![]() ) i
) i
·sin(![]()
![]() )) = 2·( cos
)) = 2·( cos![]() i
i
·sin![]() ) = 1–
) = 1–![]() ×i
×i
Ответ: Z13
= ![]() ; Z2
; Z2
= –2
Пример 4:
Z4
= 1
Число 1 запишем в тригонометрической форме
1 = 1·( cos(2pk) i
·sin(2pk)), kÎZ
Пусть Z = r×(cosj i
×sinj), тогда данное уравнение запишется в виде:
r4
×(cos4j i
×sin4j) = cos(2pk) i
·sin(2pk)), kÎZ
4j = 2pk, kÎZ
j = ![]() ,
,
kÎZ
r4
= 1
r = 1
Z = cos ![]() i
i
×sin![]()
k = 0,1,2,3…
k = 0
Z1
= cos0 i
×sin0 = 1 0 = 1
k = 1
Z2
= cos ![]() i
i
×sin![]() = 0 i
= 0 i
= i
k = 2
Z3
= cosp i
·sinp = –1 0 = –1
k = 3
Z4
= cos ![]() i
i
×sin![]()
Ответ: Z13
= ![]() 1
1
Z24
= ![]() i
i
8.ВОЗВЕДЕНИЕ В СТЕПЕНЬ И ИЗВЛЕЧЕНИЕ КОРНЯ
Из формулы 6 видно, что возведение комплексного числа r·( cosj i
·sinj) в целую положительную степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
[ r·(cosj i
·sinj)]n
= rn
·( cos nj i
·sin nj)
Число Z
называется корнем степениn
из числа w ( обозначается ![]() ), если Zn
), если Zn
=w.
Из данного определения вытекает, что каждое решение уравнения Zn
=w
является корнем степени n
из числа w. Другими словами, для того, чтобы извлечь корень степени n
из числа w, достаточно решить уравнение Zn
=w.
Если w=0, то при любом n уравнение Zn
=w
имеет только одно решение Z
= 0.
Если w![]() 0, то и Z
0, то и Z![]() 0
0
, а, следовательно, и Z и w можно представить в тригонометрической форме
Z = r·(cosj i
·sinj), w = p·(cosy i
·siny)
Уравнение Zn
= w примет вид:
rn
·( cos nj i
·sin nj) = p·( cosy i
·siny)
Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются слагаемыми, кратными 2p. Следовательно, rn
= p и nj = y 2pk,
где kÎZ или r = ![]() и j =
и j = ![]() , где kÎZ.
, где kÎZ.
Итак, все решения могут быть записаны следующим образом:
ZK
=![]() [cos(
[cos(![]() ) i
) i
·sin(![]() )], kÎZ (8)
)], kÎZ (8)
Формулу 8 называют второй формулой Муавра
.
Таким образом, если w![]() 0, то существует ровно n корней степени n из числа w: все они содержатся в формуле 8. Все корни степени n
0, то существует ровно n корней степени n из числа w: все они содержатся в формуле 8. Все корни степени n
из числа w имеют один и тот же модуль ![]() , но разные аргументы, отличающиеся слагаемым, кратным числу
, но разные аргументы, отличающиеся слагаемым, кратным числу ![]() . Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w, соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса
. Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w, соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса ![]() с центром в точке Z = 0.
с центром в точке Z = 0.
Символ ![]() не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись
не имеет однозначного смысла. Поэтому, употребляя его, следует четко представлять себе, что под этим символом подразумевается. Например, используя запись ![]() , следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i
, следует подумать о том, чтобы было ясно, понимается под этим символом пара комплексных чисел i
и –i
, или одно, то какое именно.
Уравнения высших степеней
Формула 8 определяет все корни двучленного уравнения степени n. Неизмеримо сложнее обстоит дело в случае общего алгебраического уравнения степени n:
an×Zn an–1×Zn–1 ... a1×Z1 a0=0
(9)
Где an,…,
a0
– заданные комплексные числа.
В курсе высшей математики доказывается теорема Гаусса: каждое алгебраическое уравнение имеет в множестве комплексных чисел по крайней мере один корень. Эта теорема была доказана немецким математиком Карлом Гауссом в 1779 году.
Опираясь на теорему Гаусса, можно доказать, что левая часть уравнения 9 всегда может быть представлена в виде произведения:
![]() ,
,
Где Z1
, Z2
,…, ZK
– некоторые различные комплексные числа,
а a1
,a2
,…,ak
– натуральные числа, причем:
a1
a2
… ak
= n
Отсюда следует, что числа Z1
, Z2
,…, ZK
являются корнями уравнения 9. При этом говорят, что Z1
является корнем кратности a1,
Z2
– корнем кратности a2
и так далее.
Если условиться считать корень уравнения столько раз, какова его кратность, то можно сформулировать теорему: каждое алгебраическое уравнение степени n имеет в множестве комплексных чисел ровно n корней.
Теорема Гаусса и только что сформулированная теорема дают решения о существовании корней, но ничего не говорят о том, как найти эти корни. Если корни первой и второй степени могут быть легко найдены, то для уравнений третей и четвертой степеней формулы громоздки, а для уравнений степени выше четвертой таких формул вообще не существует. Отсутствие общего метода не мешает отыскивать все корни уравнения. Для решения уравнения с целыми коэффициентами часто оказывается полезной следующая теорема: целые корни любого алгебраического уравнения с целыми коэффициентами являются делителями свободного члена.
Докажем эту теорему:
Пусть Z = k – целый корень уравнения
an
×Zn
an–1
×Zn–1
… a1
×Z1
a0
= 0
с целыми коэффициентами. Тогда
an
×kn
an–1
×kn–1
… a1
×k1
a0
= 0
a0
= – k(an
×kn–1
an–1
×kn–2
… a1
)
Число в скобках, при сделанных предположениях, очевидно, целое, значит k – делитель числа a0.
9.КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2
= a, где a – заданное действительное число, Z – неизвестное.
Это уравнение:
имеет один корень, если a = 0.
имеет два действительных корня Z1,2=![]() ,
,
если a > 0.
не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i2
×![]() =i2
=i2
×(![]() )2
)2
. Тогда уравнение Z2
= a запишется в виде: Z2
– i2
×(![]() )2
)2
= 0
т.е. (Z – i
×![]() )(Z i
)(Z i
×![]() ) = 0
) = 0
Следовательно, уравнение имеет два корня: Z1,2 = ![]() i×
i×![]()
Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами
a×Z2
b×Z c = 0
По известной общей формуле
Z1,2
=![]() (10)
(10)
Итак, при любых действительных a(a![]() 0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2
– 4×a×c
положителен , то уравнение a×Z2
b×Z c = 0 два действительных различных корня. Если D = 0, то уравнение a×Z2
b×Z c = 0 имеет один корень. Если D < 0, то уравнение a×Z2
b×Z c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1
,Z2
– корни квадратного уравнения a×Z2
b×Z c = 0, a![]() 0. Тогда справедливы свойства:
0. Тогда справедливы свойства:
Теорема Виета: Z1
Z2
= –![]()
Z1
×Z2
= ![]()
2. При всех комплексных Z справедлива формула
a×Z2
b×Z c = a×(Z – Z1
)×(Z – Z2
)
Пример 5:
Z2
– 6·Z 10 = 0
Д = b2
– 4·a·c
Д = 62
– 4·10 = – 4
– 4 = i2
·4
Z1,2
= 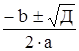
Z1,2
=![]()
Ответ: Z1
= Z2
= 3 i
Пример 6:
3·Z2
2·Z 1 = 0
Д = b2
– 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8·i2
Z1,2
=  =
= 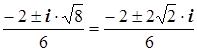
Z1,2
=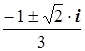
Z1
= – (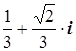 )
)
Z2
= –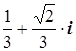
Ответ: Z1
= Z2
= –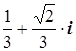
Пример 7:
Z4
– 8·Z2
– 9 = 0
Z2
= t
t2
– 8·t – 9 = 0
Д = b2
– 4·a·c = 64 36 = 100
t1,2
=  =
= ![]() = 4
= 4![]()
t1
= 9 t2
= – 1
Z2
= 9 Z2
= – 1
Z1,2
=![]() 3 Z =
3 Z = ![]()
Z3,4
=![]() i
i
Ответ: Z1,2
=![]() 3, Z3,4
3, Z3,4
=![]() i
i
Пример 8:
Z4
2·Z2
– 15 = 0
Z2
= t
t2
2·t – 15 = 0
Д = b2
– 4·a·c = 4 60 = 64
t1,2
=  =
= ![]() = –1
= –1![]() 4
4
t1
= – 5 t2
= 3
Z2
= – 5 Z2
= 3
Z2
= – 1·5 Z3,4
=![]()
![]()
Z2
= i2
·5
Z1,2
=![]() i
i![]()
Ответ: Z1,2
=![]() i
i![]()
, Z3,4
=![]()
![]()
Пример 9:
Z2
= 24 – 10·i
Пусть Z = X Y·i
(X Y·i
)2
= X2
2·X·Y·i
–Y2
X2
2·X·Y·i
– Y2
= 24 – 10·i
(X2
– Y2
) 2·X·Y·i
= 24 – 10·i
Y = – ![]()
X2
– ![]() = 24
= 24
 умножим на X2
умножим на X2![]() 0
0
X4
– 24·X2
– 25 = 0
X2
= t
t2
– 24·t – 25 = 0
t1
·t2
= – 25
t1
t2
= 24
t1
= 25 t2
= – 1
X2
= 25 X2
= – 1 — нет решений
X1,2
= ![]() 5
5
X1
= 5 X2
= – 5
Y1
= – ![]() Y2
Y2
= ![]()
Y1
= – 1 Y2
= 1
Тогда:
Z1,2
=![]() (5 – i
(5 – i
)
Ответ: Z1,2
=![]() (5 – i
(5 – i
)
ЗАДАЧИ:
1)
|
( 2 – Y)2
3·( 2 – Y)·Y Y2
= 6
4 – 4·Y Y2
6·Y – 3·Y2
Y2
= 6
–Y2
2Y – 2 = 0 /–1
Y2
– 2Y 2 = 0
Д = b2
– 4·a·c = 4 – 8 = – 4
– 4 = – 1·4 = 4· i2
Y1,2
=  =
= ![]() = 1
= 1![]() i
i
Y1
= 1– i
Y2
= 1 i
X1
= 1 i
X2
= 1– i
Ответ: {1 i
; 1– i
}
{1– i
; 1 i
}
2)
— Возведем в квадрат
— Возведем в куб
w10
×![]() 12
12
= 1
w10
×![]() 10
10
×![]() 2
2
= 1
(w×![]() )10
)10
×![]() 2
2
= 1
(![]() )10
)10
×![]() 2
2
= 1
т.к. w = A B×i
![]() = A – B×i
= A – B×i
w×![]() = (A B×i
= (A B×i
)·( A – B×i
) = A2
– (B×i
)2
= A2
B2
= ![]() 2
2
= w×![]()
т.е. ![]() 20
20
·![]() 2
2
= 1
Возьмем модуль от обоих частей последнего уравнения:
![]() 20
20
·![]() 2
2
= 1
![]() 22
22
= 1
т.е.
![]() = 1
= 1
Тогда из уравнения получим
![]() 2
2
= 1
т.е.
![]() =
= ![]() 1
1
w1
= 1 w2
= –1
Подставим эти значения в первое уравнение данной системы и найдем численное значение Z
1) w1
= 1
Z6
= 1
1 = 1·( cos(2pk) i
·sin(2pk)), kÎZ
Z = r×(cosj i
×sinj)
r6
×(cos6j i
×sin6j) = cos(2pk) i
·sin(2pk), kÎZ
r6
= 1 6j = 2pk
r = 1 j = ![]() , kÎZ
, kÎZ
Z = cos![]() i
i
·sin![]() , kÎZ
, kÎZ
k = 0,1,2…
k = 0
Z1
= cos0 i
×sin0 = 1 0 = 1
Z1
= 1
k = 1
Z2
= cos![]() i
i
·sin![]() =
= ![]() i
i
= ![]() i
i
Z2
=![]() i
i
k = 2
Z3
= cos![]() i
i
·sin![]() = –
= –![]() i
i
Z3
= –![]() i
i
k = 3
Z4
= cosp i
·sinp = –1 0 = –1
Z4
= –1
k = 4
Z5
= cos![]() i
i
·sin![]() = –
= – i
i
Z5
= – i
i
k = 5
Z6
= cos![]() i
i
·sin![]() =
=  i
i
Z6
=  i
i
Ответ: Z1
= 1, Z2
=![]() i
i
, Z3
= –![]() i
i
, Z4
= –1, Z5
= – i
i
, Z6
=  i
i
2)
w2
= –1
Z6
= –1
–1 = 1·( cos(p 2pk) i
·sin(p 2pk)), kÎZ
Пусть Z = r×(cosj i
×sinj), тогда данное уравнение запишется в виде:
r6
×(cos6j i
×sin6j) = cos(p 2pk) i
·sin(p 2pk), kÎZ
r6
= 1 6j = p 2pk
r = 1 j = ![]() , kÎZ
, kÎZ
Z = cos(![]() ) i
) i
·sin(![]() ), kÎZ
), kÎZ
k = 0,1,2…
k = 0
Z1
= cos![]() i
i
·sin![]() =
=  i
i
Z1 = i
i
k = 1
Z2
= cos(![]() ) i
) i
·sin(![]() ) = 0 i
) = 0 i
= i
Z2
=i
k = 2
Z3
= cos(![]() ) i
) i
·sin(![]() ) = –
) = – i
i
Z3
= – i
i
k = 3
Z4
= cos(![]() ) i
) i
·sin(![]() ) = –
) = – i
i
Z4
= – i
i
k = 4
Z5
= cos(![]() ) i
) i
·sin(![]() ) = 0 – i
) = 0 – i
= – i
Z5
= – i
k = 5
Z6
= cos(![]() ) i
) i
·sin(![]() ) =
) =  i
i
Z6
= i
i
Ответ: Z1
= i
i
, Z2
= i
, Z3
= – i
i
, Z4
= – i
i
, Z5
= – i
, Z6
= i
i
3)
Доказать, что сумма двух комплексных чисел не превосходит сумму модулей этих чисел.
1 СПОСОБ:
Пусть Z1
=X Y×i
и Z2
=U V×i
Доказать что:
![]()
![]()
Предположим противоположное:
![]() >
>![]() / т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
/ т.к. корень существует только из неотрицательного числа, то можно возвести в квадрат обе части неравенства.
X2
2·X·U U2
Y2
2·Y·V V2
> X2
Y2
U2
V2
2·![]()
2·(X·U Y·V) > 2·![]()
Если мы предположили верно, то X·U Y·V > 0, а поэтому возведем в квадрат:
X2
·U2
2·XU·Y·V Y2
·V2
> X2
·U2
X2
·V2
Y2
·U2
Y2
·V2
2·X·Y·V·U > X2
·V2
Y2
·U2
X2
·V2
Y2
·U2
– 2·X·Y·V·U < 0
(X·V Y·U)2
< 0
Это невозможно, т.к. A2![]() 0, значит полученное нами неравенство неверно.
0, значит полученное нами неравенство неверно.
![]()
что и требовалось доказать
2 СПОСОБ:
Пусть Z1
и Z2
– два произвольных комплексных числа. Z1
– соответствует точке A, Z2
– соответствует точке B.
В силу неравенства треугольника
![]() т.е.
т.е.
![]()
Что и требовалось доказать.
[S1]






