- Алгоритм построения логической функции по ее таблице истинности
- Алгоритм построения таблицы истинности логической функции
- Глоссарий, определения логики
- Логические операции и таблицы истинности
- Логические элементы и таблицы истинности
- Порядок выполнения логических операций в сложном логическом выражении
- Стрелка пирса
- Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
- Урок 11. алгебра логики. таблицы истинности – информатика – 10 класс – российская электронная школа
- Штрих шеффера
- Эквивалентность или логическая равнозначность
Алгоритм построения логической функции по ее таблице истинности
- Выделяют в таблице истинности строки со значением функции, равным $1$.
- Выписывают искомую формулу как дизъюнкцию нескольких логических выражений. Количество этих выражений равно количеству выделенных строк.
- Каждое логическое выражение в этой дизъюнкции записать как конъюнкцию аргументов функции.
- В случае, когда значение какого-то из аргументов функции в соответствующей строке таблицы принимает значение $0$, то этот аргумент записать в виде его отрицания.
Алгоритм построения таблицы истинности логической функции
Определяют количество строк:кол-во строк = $2^n 1$ (для строки заголовка), $n$ – количество простых выражений. Например, для функций двух переменных существует $2^2 = 4$ комбинации наборов значений переменных, для функций трех переменных – $2^3 = 8$ и т.д.
Определяют количество столбцов:кол-во столбцов = кол-во переменных кол-во логических операций. При определении количества логических операций учитывают также порядок их выполнения.
Заполняют столбцы результатами выполнения логических операций в определенной последовательности, учитывая таблицы истинности основных логических операций.
Рисунок 2.
Глоссарий, определения логики
Высказывание – это повествовательное предложение, про которое можно определенно сказать
истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции – мыслительные действия, результатом которых является изменение
содержания или объема понятий, а также образование новых понятий.
Логическое выражение – устное утверждение или запись, в которое, наряду с постоянными величинами,
обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать
одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение – логическое выражение, состоящее из одного или
нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Логические операции и таблицы истинности
1) Логическое умножение или конъюнкция:
Конъюнкция – это сложное логическое выражение, которое считается истинным в том и только том случае, когда
оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.Обозначение: F = A & B.
Таблица истинности для конъюнкции
2) Логическое сложение или дизъюнкция:
Дизъюнкция – это сложное логическое выражение, которое истинно, если хотя бы одно из
простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.Обозначение: F = A B.
Таблица истинности для дизъюнкции
3) Логическое отрицание или инверсия:
Инверсия – это сложное логическое выражение, если исходное логическое выражение истинно, то результат
отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова,
данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
4) Логическое следование или импликация:
Импликация – это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины
следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А),
а второе (В) является следствием.
Таблица истинности для импликации
5) Логическая равнозначность или эквивалентность:
Эквивалентность – это сложное логическое выражение, которое является истинным тогда
и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
Логические элементы и таблицы истинности
Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас.
Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе.
Итак, какие бывают элементы?
Элемент «И» (AND)
Иначе его называют «конъюнктор».
Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем.
Вот так выглядит элемент «И» и его таблица истинности:
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам.
Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.
Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше.
Элемент «ИЛИ» (OR)
По другому, его зовут «дизъюнктор».
Любуемся:
Опять же, название говорит само за себя.
На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули.
Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент.
Элемент «НЕ» (NOT)
Чаще, его называют «инвертор».
Надо чего-нибудь говорить по поводу его работы?
Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ».
Элемент «И-НЕ» (NAND)
Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» – единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:
Элемент «ИЛИ-НЕ» (NOR)
Та же история – элемент «ИЛИ» с инвертором на выходе.
Следующий товарищ устроен несколько хитрее:
Элемент «Исключающее ИЛИ» (XOR)
Он вот такой:
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры.
Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый.
Эквивалентная схема примерно такая:
Ее запоминать не обязательно.
Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4.
Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем.
Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 ( ). Напряжение питания – смотри в таблице в предыдущем параграфе.
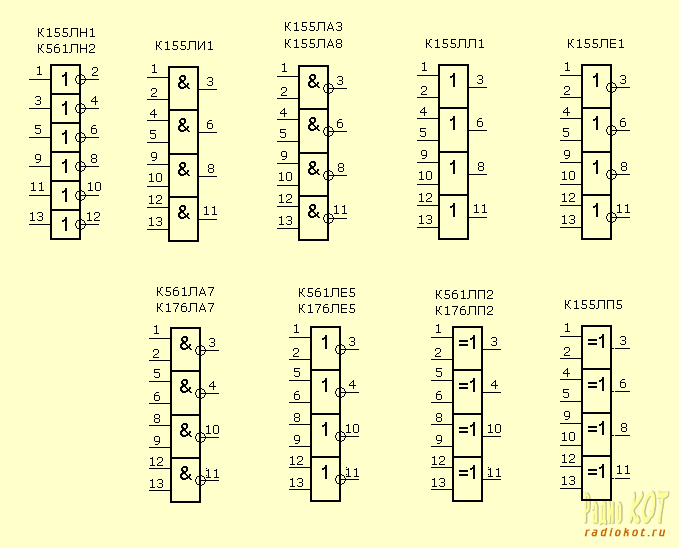
Источник: radiokot.ru
Порядок выполнения логических операций в сложном логическом выражении
- Инверсия(отрицание);
- Конъюнкция (логическое умножение);
- Дизъюнкция и строгая дизъюнкция (логическое сложение);
- Импликация (следствие);
- Эквивалентность (тождество).
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.
Стрелка пирса
Бинарная логическая операция, булева функция над двумя переменными. Названа в честь Чарльза Пирса и введена в алгебру логики в $1880—1881$ гг.
Обозначения: $downarrow$ , ИЛИ-НЕ
Таблица истинности для стрелки Пирса
Рисунок 7.
Свойства:
Стрелка Пирса, как и конъюнкция, дизъюнкция, отрицание, образует базис для булевых функций двух переменных. При помощи стрелки Пирса, можно построить все остальные логические операции, например:
$X downarrow X = ¬X$— отрицание
$(X downarrow Y) downarrow (X downarrow Y) equiv X vee Y$ — дизъюнкция
$(X downarrow X) downarrow (Y downarrow Y) equiv X wedge Y$ — конъюнкция
$((X downarrow X) downarrow Y) downarrow ((X downarrow X) downarrow Y) = X to Y$ — импликация
В электронике стрелка Пирса представлена в виде элемента, который носит название «операция 2ИЛИ-НЕ» (2-in NОR).
Строгая дизъюнкция или сложение по модулю 2 ( в теории множеств это объединение двух множеств без их пересечения)
Строгая дизъюнкция истинна, если значения аргументов не равны.
Для функции трёх и более переменных результат выполнения операции будет истинным только тогда, когда количество аргументов равных $1$, составляющих текущий набор — нечетное. Такая операция естественным образом возникает в кольце вычетов по модулю 2, откуда и происходит название операции.
Обозначения: $A oplus B$ (в языках программирования), $A≠B$, $A wedge B$ (в языках программирования).
Таблица истинности для операции сложения по модулю два
Рисунок 6.
Свойства строгой дизъюнкции:
- $a oplus 0 = a$(идемпотентность)
- $a oplus 1 = bar{a}$(отрицание)
- $a oplus a = 0$(получение 0)
- $a oplus b = b oplus a$(коммутативность)
- $(a oplus b) oplus c = a oplus (b oplus c)$(ассоциативность)
- $(a oplus b) oplus b = a$(поглощение)
- $bar{a} oplus b = a oplus bar{b} = (a equiv b)$(сравнения по модулю)
Урок 11. алгебра логики. таблицы истинности –
информатика –
10 класс –
российская электронная школа
Информатика, 10 класс. Урок № 11.
Тема — Алгебра логики. Таблицы истинности
Перечень вопросов, рассматриваемых в теме: высказывание, логическая переменная, логические операции (отрицание, конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, эквиваленция), логические выражения, предикаты и их множества истинности, таблицы истинности и их анализ.
Глоссарий по теме: импликация, эквиваленция, предикат, примеры законов алгебры логики.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса
— М.: БИНОМ. Лаборатория знаний, 2021 (с.174—197)
Открытые электронные ресурсы по теме:
http://lbz.ru/metodist/authors/informatika/3/eor10.php
http://kpolyakov.spb.ru/school/ege.htm
Теоретический материал для самостоятельного изучения:
Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.
Алгебра логики возникла в середине XIX века в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем. Логическое высказывание — это повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Например, предложение «Джордж Буль — основоположник алгебры логики» истинно, а «Солнце — спутник Земли» ложно.
Употребляемые в обычной речи логические связки «не», «и», «или», «если…то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным. Например, из двух простых высказываний (каких?) можно получить следующее составное высказывание: «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач». Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С).
Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь». Для логических значений «истина» — «ложь» могут использоваться следующие обозначения: И — Л, true — false, да — нет, 1 — 0.
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
В алгебре логики имеется шесть логических операций. Из курса информатики 8—9 классов вам знакомы три из них:
— отрицание (инверсия, логическое НЕ)
Высказыванию ставится в соответствие новое высказывание, значение которого противоположно исходному.

— конъюнкция (логическое умножение, логическое И)
Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.

— дизъюнкция (логическое сложение, логическое ИЛИ)
Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.

Рассмотрим новые логические операции.
— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией (от лат. implicatio — сплетение, тесная связь) или логическим следованием.
Операция импликации обозначается символом  и задается следующей таблицей истинности:
и задается следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если…, то». Как правило, эту связку мы используем, когда хотим показать зависимость одного события от другого.
Импликацию можно заменить на выражение, использующее ранее изученные операции НЕ и ИЛИ: 
— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.
Строгая дизъюнкция обозначается символом и задается следующей таблицей истинности:
и задается следующей таблицей истинности:

В русском языке строгой дизъюнкции соответствует связка «либо». Например, в пословице «Либо пан, либо пропал», выполнение обоих условий одновременно невозможно. В отличие от обычной дизъюнкции в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдет только одно событие.
Строгую дизъюнкцию можно представить через базовые операции следующим образом:

Чтобы доказать это равенство, достаточно для всех возможных комбинаций и
вычислить значения выражения, стоящего в правой части равенства, и сравнить их со значениями выражения
 для тех же исходных данных.
для тех же исходных данных.
— Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.
В логике эквиваленция обозначается символом  и задается следующей таблицей истинности:
и задается следующей таблицей истинности:

В разговорной речи эквивалентности соответствует связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».
Если посмотреть внимательно на таблицы истинности для двух последних логических операций, то можно заметить, что эквивалентность — это обратная операция для операции «исключающее ИЛИ», т. е. 
Можно заменить эквивалентность выражением, которое включает только базовые логические операции: 
Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.
Для логического выражения справедливо:
- всякая логическая переменная, а также логические константы (0,1) есть логическое выражение;
- если
 — логическое выражение, то и
— логическое выражение, то и  — логическое выражение;
— логическое выражение; - если A и B — выражения, то связанные любой бинарной операцией, они также представляют собой логическое выражение.
При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:
- отрицание;
- конъюнкция;
- дизъюнкция, строгая дизъюнкция;
- импликация, эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Как в математике, скобки меняют порядок выполнения операций.
Пример 1.
Дан фрагмент таблицы истинности выражения F.
x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | F |
1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Какое выражение соответствует F?
1) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8
2) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8
3) ¬(x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8
4) (x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8
Решение:
- обратим внимание, что среди значений функции только одна единица, как у операции «И», поэтому ищем правильный ответ среди вариантов, содержащих «И», «НЕ» и импликацию (варианты 1 и 3)
- вариант 1 не подходит, потому что при x6=0 в третьей строке получаем 0, а не 1
- вариант 3 подходит во всех строчках
- но давайте убедимся, что варианты 2 и 4 неправильные:
— вариант 2 исключаем, потому что при x4=1 во второй строке получаем 1, а не 0
— вариант 4 исключаем, потому что при x5=1 в первой строке получаем 1, а не 0
Ответ: 3
Пример 2.
Сколько различных решений имеет уравнение
((K L) → (L M N)) = 0
где K, L, M, N — логические переменные? В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов.
Решение
Вариант 1 (разделение на части):
— из таблицы истинности операции «импликация» следует, что это равенство верно тогда и только тогда, когда одновременно
K ˅ L = 1 и L M N = 0
— дизъюнкция ложна, только если обе переменные равны 0, поэтому для первого уравнения рассмотрим три случая:
– если K = 1 и L = 0, то второе равенство выполняется при любых М и N; поскольку существует 4 комбинации двух логических переменных (00, 01, 10 и 11), имеем 4 разных решения;
– если K = 1 и L = 1, то второе равенство выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения;
– если K = 0, то обязательно L = 1 (из первого уравнения); при этом второе равенство выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения;
— таким образом, всего получаем 4 3 3 = 10 решений.
Вариант 2 (составление таблицы истинности, достаточно трудоемкий способ):
— выражение X = ((K L) → (L M N)) зависит от четырех переменных, поэтому в таблице будет 24=16 строчек
K | L | M | N | K L | L·M·N | X |
0 | 0 | 0 | 0 | 0 | 0 | 1 |
0 | 0 | 0 | 1 | 0 | 0 | 1 |
0 | 0 | 1 | 0 | 0 | 0 | 1 |
0 | 0 | 1 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 0 | 1 | 0 | 0 |
0 | 1 | 0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 | 0 | 0 |
1 | 0 | 0 | 1 | 1 | 0 | 0 |
1 | 0 | 1 | 0 | 1 | 0 | 0 |
1 | 0 | 1 | 1 | 1 | 0 | 0 |
1 | 1 | 0 | 0 | 1 | 0 | 0 |
1 | 1 | 0 | 1 | 1 | 0 | 0 |
1 | 1 | 1 | 0 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 | 1 |
— в последнем столбце 10 нулей; это значит, что есть 10 разных комбинаций, при которых выражение X равно нулю, то есть исходное уравнение имеет 10 решений.
Ответ: 10 решений
Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х<12 становится истинным высказыванием при х=5 и ложным при х=15. Предложения такого рода называют высказывательными формами или предикатами.
Предикат — это утверждение, содержащее одну или несколько переменных.
Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката P(x)=(x<0) — множество отрицательных чисел; множество истинности предиката P(x,y)=(x2 y2=1) – множество точек окружности единичного радиуса в центре в начале координат.
Пример 3.
Рассмотрим предикат (50 < X·X) → (50 > (X 1)·(X 1)), определенный на множестве целых чисел. Найдем наибольшее число из множества истинности этого предиката.
Решение:
— задана операция импликации между двумя отношениями  и
и , решим неравенства
, решим неравенства

— обозначим эти области на оси X:

на рисунке фиолетовые зоны обозначают область, где истинно выражение A, голубая зона — это область, где истинно B
— исходя из таблицы истинности операции «импликация», заданное выражение истинно везде, кроме областей, где A = 1 и B = 0; область истинности выделена зеленым цветом
— поэтому наибольшее целое число, удовлетворяющее условию — это первое целое число, меньшее  , то есть, 7
, то есть, 7
Ответ: 7
Штрих шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Обозначения: $|$, эквивалентно операции И-НЕ.
Таблицей истинности для функции штрих Шеффера
Рисунок 8.
Свойства:
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X mid X = ¬X$ — отрицание
$(X mid Y) mid (X mid Y) = (X wedge Y)$ — конъюнкция
$(X mid X) mid (Y mid Y) = X vee Y$ — дизъюнкция
$X mid ¬X$ — константа 1
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Эквивалентность или логическая равнозначность
Эквивалентность – это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.
Обозначения: $leftrightarrow$, $Leftrightarrow$, $equiv$.
Таблица истинности для эквивалентности
Рисунок 5.
Свойства эквивалентности:
- Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
- КНФ $A equiv B = (bar{A} vee B) cdot (A cdot bar{B})$
- ДНФ $A equiv B = bar{A} cdot bar{B} vee A cdot B$







