Имитостойкость шифров. имитация и подмена сообщения.
Помимо пассивных действий со стороны противника возможны активные действия, состоящие в попытках подмены или имитации сообщения.
Если передается шифрованное сообщение y Î Y (полученное из открытого текста x Î X на ключе k Î K), то противник может заменить его на y’, отличный от y. При этом он будет рассчитывать на то, что на действующем ключе k новая криптограмма при расшифровании будет воспринята как некий осмысленный открытый текст x’, отличный от x, чем больше вероятность этого события, тем успешнее будет попытка имитации.
Имитостойкость шифра определим как его способность противостоять попыткам противника по имитации или подмене. Естественной мерой имитостойкости шифра служит вероятность соответствующего события:
Dk(y’) Î X – для попытки имитации сообщения;
(Dk(y’) Î X) Ù (y’ ¹ y) – для попытки подмены сообщения.
В соответствии с этим введем следующие обозначения:
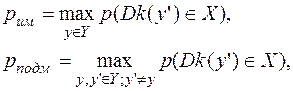
которые назовем соответственно вероятностью имитации и вероятностью подменыю Полагая, что противник выберет ту попытку, которая с большей вероятностью приводит к успеху, вводят также вероятность навязывания формулой 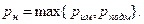
Для шифров с равновероятными ключами можно получить общие оценки введенных вероятностей.
Утверждение 1. Для шифра SB с равновероятными ключами имеет место достижимая оценка 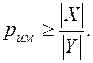 Для эндоморфного шифра с равновероятной гаммой pим = 1.
Для эндоморфного шифра с равновероятной гаммой pим = 1.
Это неравенство поясняет широко используемый для имитозащиты способ введения избыточности в передаваемое сообщение, например, дополнительных “добавок” к передаваемому сообщению типа аутентификаторов или имитовставок.
Утверждение 2. Для шифра SB с равновероятными ключами имеет место достижимая оценка
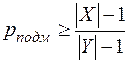 .
.
Определим совершенную имитостойкость (теоретически лучшую защиту от имитации или подмены), достижимую при данной величине |Y| множества допустимых криптограмм и при произвольном распределении P(K) на множестве ключей. Для этого вводится понятие граница Симмонса.
Обозначим через I(Y, K) взаимную информацию между Y и K, то есть величину, определяемую формулой I(Y, K) = H(Y) – H(Y / K).
Утверждение 3. Имеет место достижимая оценка
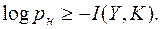
Равенство, определяемое как совершенная имитостойкость, достигается при одновременном выполнении двух условий:
1. Вероятность p(y) того, что y окажется допустимой криптограммой не зависит от y.
2. Для каждой криптограммы y Î Y вероятность p(y / k) одинакова при всех k, для которых Dk(y) Î X.
Следует отметить, что даже при совершенной имитостойкости вероятность навязывания мала лишь при большой величине I(Y, K), то есть в том случае, когда криптограмма дает значительную информацию о ключе. Информация, которую дает Y относительно K есть мера того, в какой степени ключ используется для обеспечения имитостойкости.
§
Основной причиной отсутствия какой-либо имитостойкости шифра гаммирования является то, что множество возможных открытых текстов длины l совпадает с множеством всех слов длины l в алфавите шифрвеличин. Для обеспечения имитозащиты эндоморфных шифров в открытый текст намеренно вводится избыточная информация. Это делается для выделения множества открытых текстов так, чтобы, соответствующая структура легко распознавалась, но не могла быть воспроизведена оппонентом без знания некоторого секрета, которым обычно является ключ зашифрования.
Например, к каждому сообщению перед зашифрованием можно добавить “контрольную сумму”, вычисляемую с помощью известной функции F . Отправитель сообщения вычисляет значение F от открытого текста х, присоединяет это значение к х, и шифрует полученную комбинацию. Получатель расшифровывает поступивший массив, рассматривая результат как сообщение с присоединенной контрольной суммой. После чего он применяет к полученному сообщению функцию F, чтобы, воспроизвести контрольную сумму. Если она равна контрольной сумме, поступившей с сообщением, сообщение признается подлинным (или аутентичным). Маловероятно, чтобы случайная последовательность знаков могла быть признана аутентичной.
Более надежный способ используется в военном протоколе аутентификации, принятом в США. Отправитель и получатель сообщения имеют опечатанный пакет со случайной последовательностью символов, вырабатываемой компетентным органом. Каждый из участников связи отвечает за защиту своего опечатанного пакета и имеет инструкцию не вскрывать его, пока не потребуется аутентификация сообщения. Кроме того, отправитель и получатель имеют общий секретный ключ. При аутентификации сообщения отправитель вскрывает пакет, дополняет сообщение символами этой секретной последовательности, а затем шифрует полученное сообщение, используя секретный ключ. Для шифрования обычно используется симметричный шифр. Получатель, после расшифрования сообщения (с помощью своей копии ключа) вскрывает пакет и производит аутентификацию. Сообщение интерпретируется как аутентичное только тогда, когда при расшифровании будут получены символы секретной последовательности. Если используется стойкое шифрование, то оппоненту (который не знает ключа) при осуществлении активной атаки не остается ничего другого, как случайным образом выбирать шифртекст в надежде, что он будет принят получателем как аутентичный. Если секретная последовательность состоит, например, из r битов, то вероятность того, что при расшифровании случайно выбранный оппонентом “шифрованный текст” даст со общение, заканчивающееся неизвестной ему, но правильной последовательностью, будет составлять величину 2–r.
§
Другой метод нашел распространение при аутентификации электронной передачи фондов в Федеральной резервной системе США. Подобные передачи должны быть аутентифицированы с использованием процедуры, которая фактически реализована в криптографическом алгоритме, определенном в стандарте шифрования данных США (ранее DES, теперь — AES). Аутентификатор генерируется в режиме, называемом шифрованием со сцеплением блоков. В этом режиме сообщение разбивается на 64 битные блоки – М = M1M2…Мn, которые последовательно шифруются следующим образом. Блоки шифртекста С1,С2,… вырабатываются по рекуррентной формуле
Сi = Еk (Ci-1 Å М,),
при этом вектор С0 полагается равным начальному вектору IV (Initial Vector). Начальный вектор меняется ежедневно и хранится в секрете. Схематично этот режим изображается следующим образом:
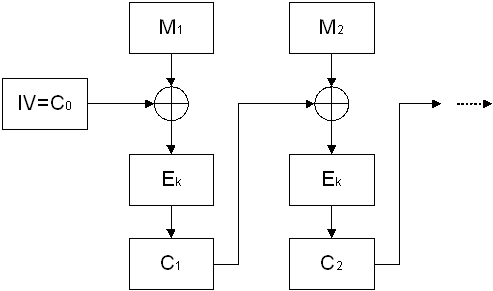
Рис.11. Режим выработки имитовставки.
Процедура повторяется до тех пор, пока не будут обработаны все блоки текста. Последний блок шифртекста — Сn является функцией секретного ключа, начального вектора и каждого бита текста, независимо от его длины. Этот блок называют кодом аутентичности сообщения (КАС), и добавляют к сообщению в качестве аутентификатора. Само расширенное аутентификатором сообщение передается обычно открытым, хотя может быть и зашифрованным, если требуется секретность. Любой владелец секретного ключа и начального вектора может проверить правильность такого аутентификатора. Нужно лишь повторить ту же процедуру шифрования. Оппонент, однако, не может ни осуществить генерацию аутентификатора, который бы воспринимался получателем как подлинный, для добавления его к ложному сообщению, ни отделить аутентификатор от истинного сообщения для использования его с измененным или ложным сообщением. В обоих случаях вероятность того, что ложное сообщение будет интерпретироваться как подлинное, равна вероятности “угадывания” аутентифкатора, то есть 2-64. Подчеркнем, что предложенный способ делает аутентификатор сложной функцией информации, которую он аутентифицирует. В таком случае подмножество допустимых сообщений состоит из тех пар текст-КАС, которые могут успешно пройти проверку на соответствие аутентификатора тексту с использованием ключа.
Оба способа имитозащиты передаваемых сообщений, связанные с введением избыточности, моделируются так называемыми кодами аутентификации (или А-кодами). В том случае, когда расширенное аутентификатором сообщение шифруется, говорят об А-кодах с секретностью. Если расширенное сообщение передается в открытом виде, говорят об А-кодах без секретности.
Вопросы использования криптографических хэш-функций для обеспечения имитостойкости будут рассматриваются подробнее в соответствующем разделе лекцийю.
§
Помимо целенаправленных искажений передаваемой шифрованной информации возможны также искажения, происходящие за счет наличия помех в канале связи. Такие помехи могут привести к искажениям и даже потере некоторых знаков используемого алфавита. Если искаженный знак не является знаком используемого алфавита, то на приеме факт искажения легко установить. В противном случае факт искажения может быть установлен лишь при расшифровании, когда искажение в шифртексте ведет к потере части или даже всего открытого текста. Так же проявляется и потеря знаков шифртекста.
Прежде всего интересен вопрос о свойствах самого шифра, позволяющих не распространять искажений при расшифровании. Ограничимся только рассмотрением эндоморфных (X=Y) шифров и искажений двух типов:
1. Замена знаков знаками того же алфавита.
2. Потеря знаков или появление дополнительных знаков того же алфавита.
Шифры, не распространяющие искажений типа “замена знаков”.
Будем рассматривать шифры, описываемые алгебраической моделью
SA = (X, K, Y, E, D),
в которой 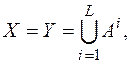 причем для любых x Î X и k Î K длина y = Ek(x) совпадает с длиной x.
причем для любых x Î X и k Î K длина y = Ek(x) совпадает с длиной x.
Мерой значительности последствий искажений типа “замена знаков” является метрика на множестве сообщений X = Y. Простейшей является метрика Хэмминга m,определяемая формулой
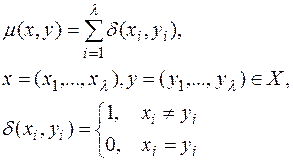
Так как для эндоморфного шифра каждое правило зашифрования Ek представляет собой биекцию Ek : X ® X, то будем пользоваться подстановочной моделью шифра – SП = (X, E),в которой множество E ={ek : k Î K} рассматривается как множество подстановок e : X ® X, e Î E.
Шифр SП = (X, E)не распространяет искажений типа замены знаков и являются помехостойкими если для любых x, y Î Al и любого e Î E выполняется неравенство
m(e-1x, e-1y) £ m(x, y).
Подстановки e Î E, удовлетворяющие предыдущему равенству, называются изометриями на X.
Теорема А. А. Маркова. Биекция eÎE является изометрией на X тогда и только тогда, когда 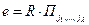 для подходящих преобразований множества X:
для подходящих преобразований множества X:
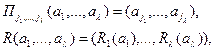
где (j1,…,jl) – перестановка чисел 1, 2, …, l; Ri Î S(A) – некоторые фиксированные подстановки множества A, ai Î A, 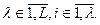
Согласно теореме Маркова, в классе эндоморфных шифров, не изменяющих длины сообщений, не распространяют искажения типа замены знаков, например шифры перестановки, поточные шифры однозначной замены, а также их композиции типа шифр замены – шифр перестановки.
Шифры, не распространяющие искажений типа “пропуск-вставка знаков”.
Приведем теорему, рассматривающую подстановочную модель шифра.
Теорема. Если SП = (X, E)– шифр не распространяющий искажений типа пропуск-вставка, то для любого e Î E, либо e = pL, либо у = pL· f (при подходящем p Î S(A)), где pL отображение множества X в себя, определенное для любого a = (a1,…,al) Î X формулой
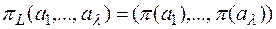
(p – некоторая подстановка множества A), а f – отображение множества X в себя, меняющее порядок следования букв любого слова на противоположный:
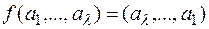
Всякий шифр, не распространяющий искажений типа “пропуск-вставка знака” есть либо шифр простой замены либо произведение шифра простой замены и частного вида шифра перестановки, заключающейся в инверсной записи текста (справа налево).
Следовательно, все сложные шифры распространяют искажения типа “пропуск-вставка” и в данном случае борьба с такими искажениями криптографическими методами невозможна и, следовательно, необходимо применять иные способы повышения помехоустойчивости (например, введением избыточности – контрольные суммы и пр.).
Практические вопросы повышения надежности.
Совместно с алгоритмом шифрования данных целесообразно использовать алгоритм сжатия по следующим причинам:
· Криптоанализ опирается на избыточность шифртекста, а сжатие файла перед шифрованием эту избыточность снижает;
· Шифрование занимает много времени, а потому сжатие файла до шифрования ускоряет весь процесс.
Важно запомнить, что сжатие должно выполняться именно до шифрования. (Сжимаемость шифртекста можно использовать как неплохой тест алгоритма шифрования. Если шифртекст можно сжать, значит алгоритм не сишком надежен.)
Вырабатывать имитовставку можно до сжатия файла и сжимать вместе с ним с целью повышения стойкости шифра. (Имитовставка повышает избыточность текста.) Или же выполнять после шифрования, с целью ускорения процесса аутентификации сообщения.
Помехоустойчивое кодирование, повышающее избыточность текста, наоборот целесообразно применять после шифрования данных.
Последовательность применения имитовставки и кодирования приведена на рис.12.

Рис. 12. Практическое применение имитовставки в сочетании со сжимающим и помехоустойчивым кодированием.
Контрольные вопросы
1. Назовите основные составляющие алгебраической модели шифра.
2. Для чего применяются вероятностные модели шифров?
3. Для чего применяются модели открытых текстов?
4. Назовите критерии на открытый текст.
5. В чем различие между теоретической и практической криптостойкостью шифров?
6. В чем различие между имитацией и подменой сообщения?
7. Назовите основные способы обеспечения имитостойкости.
8. Какие бывают виды искажений при передаче сообщения?
§
Алфавитом, на котором действует блочный шифр, является множество двоичных векторов-блоков открытого текста одинаковой длины (64, 128 и т.д.). Так как с увеличением мощности алфавита энтропия на один знак также увеличивается, криптографическая стойкость алгоритма возрастает. Блочные шифры реализуются путем многократного применения к блокам открытого текста некоторых базовых преобразований.
Требования к базовым преобразованиям :
· возможность простой реализации (как аппаратной, так и программной);
· способность давать при небольшом числе итераций аналитически сложные преобразования;
· соответствие критериям рассеивания и перемешивания;
· соотвествие критерию лавинного эффекта.
Принцип лавинного эффекта – применение шифрующего преобразования к наборам аргументов, отличающихся в незначительном числе позиций, должно приводить к к существенному изменению результата.
Принцип перемешивания (diffusion)- криптографические преобразования должны обеспечивать максимальное усложнение статистической и аналитической взаимосвязи между открытым текстом и шифртектсом.
Принцип рассеивания (confusion) – криптографические преобразования должны обеспечивать максимальное усложнение статистической и аналитической взаимосвязи между шифртекстом и ключом.
Перемешивающие преобразования – сложные в криптографическом отношении локальные преобразования, над отдельными частями шифрующих блоков.
Рассеивающие преобразования – простые преобразования, переставляющие между собой части блоков текста.
Применяемые математические преобразования (операции):
· Перестановки –смена местами битовых значений разрядов подблоков на основе фиксированных подстановок.
· Битовые сдвиги – (X >>Y) сдвиг вправо и (X<<Y) сдвиг влево битовых значений разрядов подблока X (соответствует умножению на 2 и целочисленному делению на 2 ) на величину, определяемую значением подблока Y.
· Циклические битовые сдвиги – (X>>>Y) циклический сдвиг вправо и (X<<<Y) циклический сдвиг влево битовых значений разрядов подблока X (ключа, шифртекста) на величину, определяемую значением подблока Y.
· S-подстановки – подстановки значений на основе матриц подстановки, где элементы битового блока используются в качестве параметров (координат элементов) матрицы подстановки. S-подстановки могут быть сужающими, расширяющими и однозначными в зависимости от размерного соотношения (в битах) входных и выходных подблоков данных.
· Побитовая инверсия – (~X) инверсия всех битовых регистров блока X.
· Побитовое сложение по модулю 2 – (XÅY) операция XOR над всеми битовыми регистрами подблоков X и Y.
· Сложение по модулю 2n (n – длина блока в битах) – (X Y) двоичное сложение подблоков с отбрасыванием значений старших регистров переноса.
Y) двоичное сложение подблоков с отбрасыванием значений старших регистров переноса.
· Умножение по модулю 2n 1 – (XY) двоичное умножение с отбрасыванием значений старших регистров переноса, причем нулевое значение подблока принимается равным 0 = 2n.
· Сложные операции (нелинейние подстановки , логарифмирование и экспоненцирование в конечном поле и пр.).
Сеть Файстеля.
Сеть Файстеля служит структурной основой построения большинства современных блочных криптоалгоритмов и является по сути методом смешивания текущей части шифруемого блока с результатом некоторой функции, вычисленной от другой независимой части того же блока. Эта методика получила широкое распространение, поскольку обеспечивает выполнение требования о многократном использовании ключа и материала исходного блока информации.
Действие, состоящее из однократного вычисления образующей функции и последующего наложения ее результата на другую ветвь с обменом их местами, называется циклом или раундом (англ. round) сети Файстеля. Оптимальное число раундов N – от 8 до 32. Важно то, что увеличение количества раундов значительно увеличивает криптостойстость любого блочного шифра к криптоанализу.
Классическая схема одного раунда сети Файстеля имеет следующую структуру:

Зашифрование:
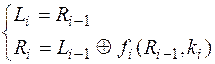
Расшифрование:

Рис.13. Сеть Файстеля
Независимые потоки информации, порожденные из исходного блока, называются ветвями сети. В классической схеме их две. Функция f называется образующей.
Данная схема является обратимой. Сеть Файстеля обладает тем свойством, что даже если в качестве образующей функции f будет использовано необратимое преобразование, то и в этом случае вся цепочка будет восстановима. Это происходит вследствие того, что для обратного преобразования сети Файстеля не нужно вычислять функцию f-1.
Благодаря применению финального преобразования (перестановка левой и правой частей блока) сеть Файстеля симметрична. Использование операции XOR, обратимой своим же повтором, и инверсия последнего обмена ветвей делают возможным раскодирование блока той же сетью Файстеля, но с инверсным порядком применения подключей ki. Заметим, что для обратимости сети Файстеля не имеет значение является ли число раундов четным или нечетным числом. В большинстве реализаций схемы, в которых оба вышеперечисленные условия (операция XOR и уничтожение последнего обмена) сохранены, прямое и обратное преобразования производятся одной и той же процедурой.
В настоящее время чаще применяют модификацию сети Фейстеля для большего числа ветвей. Это в первую очередь связано с тем, что при больших размерах кодируемых блоков (128 и более бит) становится неудобно работать с математическими функциями по модулю 64 и выше. Как известно, основные единицы информации обрабатываемые процессорами на сегодняшний день – это байт и двойное машинное слово 32 бита. Поэтому все чаще и чаще в блочных криптоалгоритмах встречается сеть Фейштеля с 4-мя ветвями. Самый простой принцип ее модификации изображен на рисунке а). Для более быстрого перемешивания информации между ветвями (а это основная проблема сети Фейштеля с большим количеством ветвей) применяются две модифицированные схемы, называемые “type-2” и “type-3”. Они изображены на рис.14.
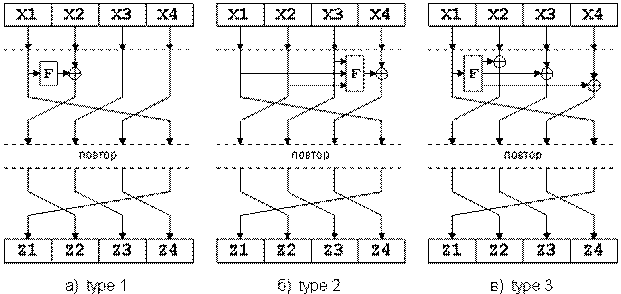
Рис.14. Сеть Файстеля на четыре ветви.
§
Основные параметры блочных криптоалгоритмов.
Основными параметрами, характеризующими современные блочные криптографические алгоритмы являются размер блока шифртекста (определяющий энтропию алфавита сообщения), размер ключевого пространства (определяющий энтропию криптосистемы), количество раундов, структурная схема криптоалгоритма, применяемые криптографические преобразования (математические операции). Характеристики некоторых наиболее известных современных блочных криптоалгоритмов сведены в таблицу .
Таблица 6. Основные параметры распространенных блочных криптоалгоритмов.
| № | Название | Размер блока, бит | Размер ключа, бит | Кол-во раундов | Основа алгоритма | Применяемые операции |
| DES | Сеть Файстеля (2 ветви) | XOR, S-подстановки, перестановки | ||||
| 3DES | 112,168 | Алгоритм DES | -‘- | |||
| IDEA | Мультипликативно-аддитивная структура (4 ветви) | XOR, сложение по модулю 216, умножение по модулю 216 1 | ||||
| Blowfish | 32..448 | Модифицированная сеть Файстеля (2 ветви) | XOR, сложение по модулю 232 , S-подстановки | |||
| RC5 | 32, 64, 128 | 8..2040 | 1.255 | Оригинальная структура (2 ветви) | XOR, сложение/вычитание, циклический сдвиг | |
| CAST | 64,128 | 40..256 | 3..32 | Сеть Файстеля с переменной F (2 ветви) | XOR, сложение/вычитание, циклический сдвиг, S-подстановки | |
| RC2 | 8..1024 | Оригинальная структура (4 ветви) | XOR, сложение, циклический сдвиг, побитовое “И”, побитовое дополнение | |||
| ГОСТ 28147-89 | Сеть Файстеля (2 ветви) | XOR, сложение, циклический сдвиг, S-подстановки | ||||
| TEA | Несимметричная сеть Файстеля (2 ветви) | XOR, сложение, битовый сдвиг | ||||
| MARS | 128,192,256 | 16 16 | Сеть Файстеля (4 ветви) | XOR, сложение, циклический сдвиг, S-подстановки | ||
| RC6 | 128,192,256 | Сеть Файстеля (4 ветви) | XOR, сложение, циклический сдвиг, преобразование T | |||
| № | Название | Размер блока, бит | Размер ключа, бит | Кол-во раундов | Основа алгоритма | Применяемые операции |
| Serpent | 128,192,256 | Сеть Файстеля (4 ветви) | XOR, битовый сдвиг, циклический сдвиг, S-подстановки | |||
| Twofish | 128,192,256 | ? | Алгоритм Blowfish, сеть Файстеля (4 ветви), преобразование Адамара | XOR, сложение, циклический сдвиг, S-подстановки | ||
| Rijndael (AES) | 128,192,256 | 10..14 | Табличные преобразования подблоков | XOR, S-подстановки, сдвиг строк, перемешивание в столбцах | ||
| Base King | ? | ? | Алгоритм 3-WAY | ? | ||
| SAFER | 64,128 | ? | Итеративные раунды, псевдопреобразования Адамара | Логарифмирование и экспоненцирование в конечном поле, XOR, сложение | ||
| 3-WAY | ? | Оригинальная процедура | Линейная подстановка на основе сдвигов и XOR, перестановки, нелинейная подстановка 3-бит блоков |
Ниже рассмотрим подробнее некоторые современные блочные криптоалгоритмы
Алгоритм DES.
DES представляет собой 64-битовый блочный алгоритм с 56-битовым ключом. Как и ГОСТ он построен на классической сети Файстеля и выполняется в течение 16 раундовсм рис.15, кроме того, он имеет начальную и завершающую перестановки.
При подстановке через S-блок на вход подается 48-битовый блок, разбитый восемь 6-битовых подблока, соответствующие каждый своей S-матрице. Первый и последний биты подблока объединяются в 2-битовое число, определяющее строку S-матрицы, а средние 4 бита объединяются в 4-битовое число, определяющее столбец. На выход подается 4-битовое значение соответствующего элемента S-матрицы.
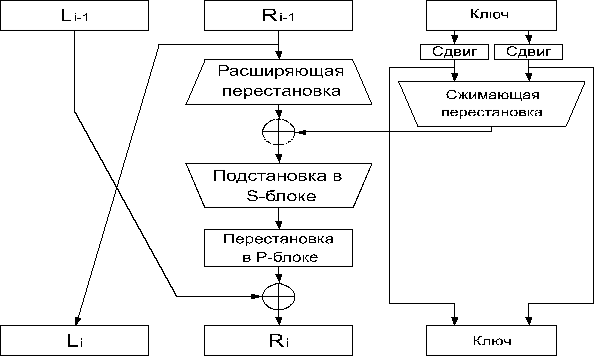
Рис.15. Раунд шифрования DES
Алгоритм DES являлся коммерческим стандартом шифрования США до 2000 года, когда ему на смену пришел AES. В настоящее время алгоритм применяется в варианте 3DES – каждый блок шифруется трижды на разных ключах. Фактическая длина ключа составила 168 бит.
Блочный шифр TEA
Один из самых простых в реализации, но признанно стойких криптоалгоритмов – TEA (Tiny Encryption Algorithm).
Параметры алгоритма:
Размер блока – 64 бита.
Длина ключа – 128 бит.
В алгоритме использована сеть Фейстеля с двумя ветвями в 32 бита каждая.
Образующая функция F обратима.
Сеть Файстеля несимметрична из-за использования в качестве операции наложения не исключающего “ИЛИ”, а арифметического сложения.
Ниже приведен код криптоалгоритма на языке программирования PASCAL.
type TLong2=array[0.. 1] of longint; TLong2x2=array[0.. 1] of TLong2;const Delta=$9E3779B9;var key:TLong2x2;procedure EnCryptRouting(var data);var y,z,sum:longint; a:byte;beginy:=TLong2(data)[0];z:=TLong2(data)[1];sum:=0;for a:=0 to 31 do begin inc(sum,Delta); inc(y,((z shl 4) key[0,0]) xor (z sum) xor ((z shr 5) key[0,1])); inc(z,((y shl 4) key[1,0]) xor (y sum) xor ((y shr 5) key[1,1])); end;TLong2(data)[0]:=y;TLong2(data)[1]:=zend;
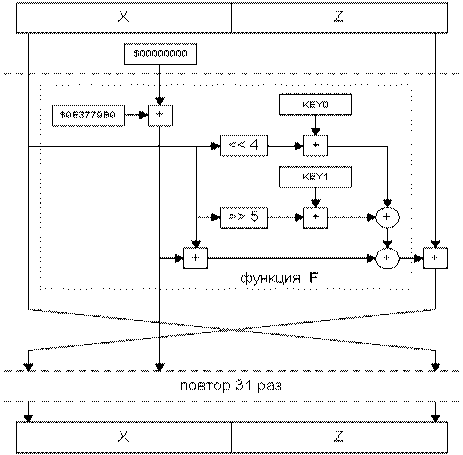
Рис.16. Алгоритм TEA
Отличительной чертой криптоалгоритма TEA является его размер. Простота операций, отсутствие табличных подстановок и оптимизация под 32-разрядную архитектуру процессоров позволяет реализовать его на языке ASSEMBLER в предельно малом объеме кода. Недостатком алгоритма является некоторая медлительность, вызванная необходимостью повторять цикл Фейштеля 32 раза (это необходимо для тщательного “перемешивания данных” из-за отсутствия табличных подстановок).
Схема работы алгоритма приведена на рис. 15.
§
Данный алгоритм получает на входе 64-битовый блок открытого текста (в процессе шифрования он разбивается на четыре 16-битовых подблока) и 128-битовый ключ, из которого генерируется пятьдесят два 16-битовых подключа шифрования Z1..Z52 по шесть подключей на каждый из восьми раундов и четыре подключа для выходного преобразования. На выходе генерируется 64-битовый блок шифрованного текста. Алгоритм расшифрования IDEA полностью повторяет структуру алгоритма шифрования: в качестве входных данных использует 64-битовый блок шифрованного текста, и тот-же 128-битовый ключ, из которого генерируются пятьдесят два 16-битовых подключей расшифрования U1..U52. В результате работы алгоритм расшифрования должен генерировать 64-битовый блок открытого текста.
Алгоритм шифрования представляет собой сложную комбинацию смешанного использования трех различных операций. Каждая из операций предполагает два 16-битовых входных значения, в результате обработки которых получается одно 16-битовое выходное значение. Вот эти операции:
Побитовое исключающее “ИЛИ” (XOR, сумма по модулю 2), обозначаемое символом Å.
Сложение целых чисел по модулю 216 (по модулю 65536) с входными и выходными значениями, рассматриваемыми как 16-битовые целые числа без знака. Эта операция обозначается символом  .
.
Умножение целых чисел по модулю 216 1 (по модулю 65537) с входными и выходными значениями, рассматриваемыми как 2-битовые целые числа без знака, за исключением блока состоящего из одних нулей, который интерпретируется как 216. Эта операция обозначается символом .
Упрощенно операция реализуется следующим отображением:
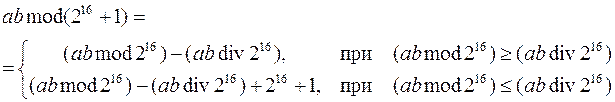
Обратите внимание, что (ab mod 216) соответствует 16 наименее значимым битам ab, а (ab div 216) является простым сдвигом ab вправо на 16 битов. Особенность данной операции в том, что она образует группу (т. е. каждый элемент обратим, включая 0 º 216). Эти операции являются несогласованными: 1) Никакие две из этих трех операций не подчиняются дистрибутивному закону. 2) Никакие две из этих трех операций не подчиняются ассоциативному закону.
Вычисление подключей IDEA.
В алгоритме IDEA используется 128-битовый ключ Z, который должен быть как у отправителя, так и у получателя сообщения. Из этого до начала шифрования или расшифрования генерируются пятьдесят два 16-битовых подключа. При этом применяется следующая схема. Первые восемь подключей, обозначенные Z1..Z8, образуются непосредственно из ключа: Z1 равен первым 16 битам ключа, Z2 – следующим 16 и т.д.
Затем к ключу шифрования применяется циклический сдвиг влево на 25 битов и создается восемь следующих подключей. Эта процедура повторяется до тех пор, пока не будут получены все 52 подключа. В таблице показано соответствие битов всех подключей битам исходного ключа.
Подключи расшифрования U1..U52 получаются из ключей шифрования по схеме, приведенной в таблице. Где
Zi-1 – мультипликативное обращение Zi по модулю 216 1 (простое число) то есть
Zi Zi-1 = 0000000000000001.
-Zi – аддитивное обращение Zi по модулю 216 то есть
Zi (-Zi) = 0000000000000000.
(-Zi) = 0000000000000000.
1. Первых четыре подключa для i-го раунда дешифрования получаются из первых четырех подключей (10 – i)-гo раунда шифрования, если 9-м раундом считать выходное преобразование. Первый и четвертый подключи дешифрования равны мультипликативным обращениям по модулю 216 1 первого и четвертого подключей шифрования соответственно. Для раундов со 2-го по 8-й второй и третий подключи дешифрования равны аддитивным обращениям по модулю 216 третьего и второго подключей шифрования соответственно. Для раундов 1 и 9 второй и третий подключи дешифрования равны аддитивным обращениям по модулю 216 второго и третьего подключей шифрования соответственно.
2. Для первых восьми раундов два последних подключа i-го раунда дешифрования равны двум последним подключай (9 – i)-го раунда шифрования.
§
Процесс шифрования предполагает два раунда и выходное преобразование. Один раунд состоит из преобразования входных блоков и субшифрования см рис. 17. Основой субшифрования является основной строительный блок алгоритма – мультипликативно-аддитивная (МА) структура.
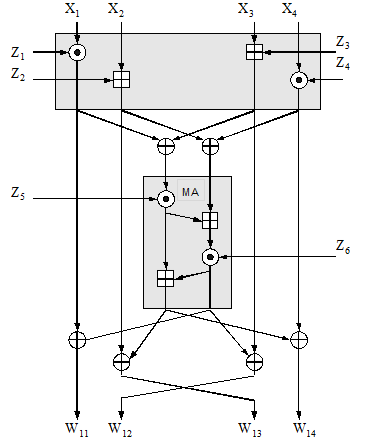
Рис.17. Раунд шифрования IDEA
Раунд начинается с преобразования, которое с помощью операции сложения и умножения связывает четыре входных подблока с четырьмя подключами. Это преобразование представлено серым прямоугольником вверху рисунка. Четыре выходных блока этого преобразования связываются операцией XOR с целью получения двух 2-битовых блоков, которые затем подаются на вход структуры МА, представленной на рисунке нижним серым прямоугольником. Кроме того, структура МА получает на входе два подключа, а в результате обработки всех полученных данных на выходе этой структуры генерируется два 2-битовых значения.
Наконец, четыре блока, полученных на выходе первого преобразования связываются с помощью операции XOR с двумя блоками, полученными на выходе структуры МА, и в результате имеется четыре выходных блока (W11..W14) данного раунда см. рис.18
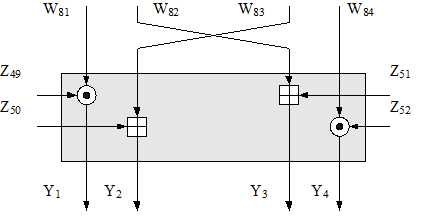
Рис.18. Выходное преобразование IDEA.
Выходное преобразование имеет структуру, подобную структуре той части предыдущего раунда шифрования, которая представлена на рисунке верхним серым прямоугольником. Единственное отличие в том, что второй и третий входные подблоки перед обработкой меняются местами. Фактически это означает отмену операции обмена, выполненной в конце второго раунда. Наличие этих лишних, по сути, перестановок обеспечивает возможность использования одной и той же структуры как для шифрования, так и для расшифрования. Кроме того, в отличие от предыдущих раундов на данной стадии используется не шесть подключей, а только четыре.
Подробно рассмотрим работу алгоритма. Выходы первого раунда расшифрования обозначим как (V11..V14). Промежуточные выходы первого раунда зашифрования и расшифрования обозначим соответственно как (I11..I14) и (J11..J14).
При шифровании на выходе функции выходного преобразования имеем
Y1 = W81Z49, Y2 = W83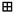 Z50, Y1 = W82
Z50, Y1 = W82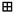 Z51, Y4 = W84Z52.
Z51, Y4 = W84Z52.
При расшифровании на выходе первой подстадии первого раунда получаем
J11 = Y1U1, J12 = Y2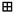 U2, J13 = Y3
U2, J13 = Y3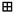 U3, J14 = Y4U4.
U3, J14 = Y4U4.
Заменив соответствующие значения эквивалентными получим
J11 = Y1Z49-1 = W81 Z49Z49-1= W81,
J12 = Y2 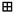 -Z50 = W83
-Z50 = W83 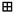 Z50
Z50 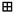 -Z50 = W83,
-Z50 = W83,
J13 = Y3 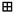 -Z51 = W82
-Z51 = W82 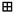 Z51
Z51 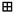 -Z51 = W82,
-Z51 = W82,
J14 = Y4Z52-1 = W84 Z52Z52-1= W84.
Таким образом выходные значения первой подстадии первого раунда расшифрования совпадают с входными данными последней стадии шифрования за исключением того, что второй и третий блок оказываются переставленными. Следующие соотношения:
W81 = I81ÅMAR(I81ÅI83, I82ÅI84),
W82 = I83ÅMAR(I81ÅI83, I82ÅI84),
W83 = I82ÅMAL(I81ÅI83, I82ÅI84),
W84 = I84ÅMAL(I81ÅI83, I82ÅI84),
Где MAR(X, Y) обозначает правое выходное значение структуры МА для входных значений X и Y, а MAL(X, Y) соответственно левое выходное значение. Тогда
V11 = J11ÅMAR(J11ÅJ13, J12ÅJ14) =
= W81ÅMAR(W81ÅW82, W83ÅW84) =
= I81ÅMAR(I81ÅI83, I82ÅI84) Å MAR [I81ÅMAR(I81ÅI83, I82ÅI84) Å I83ÅMAR(I81ÅI83, I82ÅI84),
I82ÅMAL(I81ÅI83, I82ÅI84) Å I84ÅMAL(I81ÅI83, I82ÅI84)] =
= I81ÅMAR(I81ÅI83, I82ÅI84) Å MAR(I81ÅI83, I82ÅI84) =
= I81.
Точно так же получаем V11 = I81, V12 = I83, V13 = I82, V14 = I84. Таким образом, выходные данные второй подстадии процесса расшифрования совпадают с входными значениями предпоследней стадии процесса шифрования за исключением перестановки второго и третьего блоков. Далее можно показать, что соотношение сохраняется для всех последующих подстадий вплоть до V81 = I11, V82 = I13, V83 = I12, V84 = I14. Наконец входное преобразование процесса расшифрования эквивалентно преобразованию первой подстадии шифрования за исключением перестановки 2-3 блоков и результаты зашифрования/расшифрования совпадут.
§
Алгоритм – победитель конкурса AES, объявленный в 2000 году, был разработан двумя бельгийскими криптографами Дименом (Daemen) и Рийменом (Rijmen). Эта криптосистема не является обобщением шифра Фейстеля. В основе алгоритма – повторяющиеся раунды, каждый из которых состоит из замен, перестановок и прибавления ключа. Кроме того, AES использует сильную математическую структуру: большинство его операций основано на арифметике поля 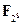 . Однако в отличие от DES зашифрование и расшифрование в этом алгоритме – процедуры разные. Элементы поля
. Однако в отличие от DES зашифрование и расшифрование в этом алгоритме – процедуры разные. Элементы поля 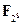 хранятся в памяти компьютера в виде 8-битовых векторов (байтов). Например последовательность ‘1000 0011b’ соответствует многочлену X 7 X 1 над полем F2 или шестнадцатиричному числу ‘83h’.
хранятся в памяти компьютера в виде 8-битовых векторов (байтов). Например последовательность ‘1000 0011b’ соответствует многочлену X 7 X 1 над полем F2 или шестнадцатиричному числу ‘83h’.
Арифметические операции в поле 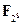 соответствуют операциям над двоичными многочленами из F2[X] по модулю неприводимого многочлена
соответствуют операциям над двоичными многочленами из F2[X] по модулю неприводимого многочлена
m(X) = X 8 X 4 X 3 X 1.
В алгоритме AES 32-битовые слова отождествляются с многочленами степени 3 из 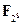 [X]. Отождествление делается в формате «перевертыш», то есть сташий бит соответствует младшему коэффициенту многочлена. Так, например, слово
[X]. Отождествление делается в формате «перевертыш», то есть сташий бит соответствует младшему коэффициенту многочлена. Так, например, слово
a0||a1||a2||a3
соответствует многочлену
a3X 3 a2X 2 a1X a0.
Арифметика в алгоритме совпадает с арифметическими действиями в кольце многочленов 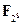 [X] по модулю многочлена M(X) = X 4 1. Заметим, что многочлен M(X) = (X 1)4 приводим, и, следовательно, арифметические действия в алгоритме отличны от операций поля, в частности, бывают пары ненулевых элементов, произведение которых равно 0.
[X] по модулю многочлена M(X) = X 4 1. Заметим, что многочлен M(X) = (X 1)4 приводим, и, следовательно, арифметические действия в алгоритме отличны от операций поля, в частности, бывают пары ненулевых элементов, произведение которых равно 0.
AES – настраиваемый блочный алгоритм, который может работать с блоками из 128, 192 или 256 битов. Для каждой комбинации размера блока и размера ключа определено свое количество раундов. Здесь рассматривается самый простой вариант алгоритма, при котором блоки, как и ключ, состоят из 128 битов. В этом случае в алгоритме выполняется 10 раундов.
Алгоритм оперирует с внутренней байтовой матрицей размера 4 на 4, называемой матрицей состояний:
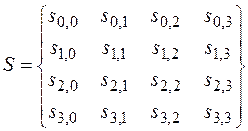 ,
,
которую обычно записывают как вектор 32-битовых слов. Каждое слово в векторе представляет собой столбец матрицы. Подключи также хранятся в виде матрицы 4 на 4:
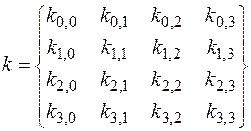 .
.
§
Раундовая функция алгоритма действует с использованием четырех операций.
SubBytes. В алгоритме есть два типа S-блоков. Один применяется при зашифровании, а другой – при расшифровании. S-блоки имеют прозрачную математическую структуру. Они поочередно обрабатывают строки матрицы состояний s = [s7, …, s0], воспринимая их как элементы поля 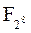 . Их работа состоит из двух шагов.
. Их работа состоит из двух шагов.
1. Вычисляется мультипликативный обратный к элементу 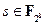 и записывается как новый байт x = [x7, …, x0]. По соглашению, элемент [0, …, 0], не имеющий обратного, остается неизменным.
и записывается как новый байт x = [x7, …, x0]. По соглашению, элемент [0, …, 0], не имеющий обратного, остается неизменным.
2. Битовый вектор x при помощи линейного преобразования над полем F2 переводится в вектор y:
 ,
,
служащий выходом S-блока. Действия S-блока на стадии расшифрования состоят в обратном линейном преобразовании и вычислении мультипликативного обратного. Эти преобразования байтов можно осуществить, используя табличный поиск или микросхему, реализующую вычисление обратных элементов в 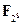 и линейные преобразования.
и линейные преобразования.
ShiftRows. Операция осуществляет циклический сдвиг матрицы состояний. Каждая из ее строк сдвигается на свое число позиций. В рассматриваемой версии шифра это преобразование имеет вид:
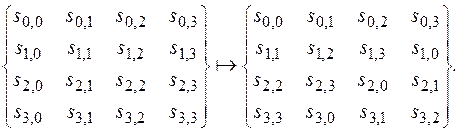
Обратная операция – тоже циклический сдвиг, но в противоположном направлении. Данная операция является рассеивающим преобразованием на протяжении нескольких раундов.
MixColumns. Операция в сочетании с предыдущей является рассеивающим преобразованием и обеспечивает зависимось каждого выходного байта от каждого входного.
Каждый столбец матрицы представляется в виде многочлена степени 3 с коэффициентами из 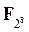 :
:
a(X) = a0 a1X a2X2 a3X3.
Новый столбец получается умножением многочлена a(X) на фиксированный многочлен
с(x) = ‘02h’ ‘01h’· X ‘01h’· X2 ‘03h’· X3.
по модулю многочлена M(X) = X 4 1. Так как умножение на многочлен линейная операция, ее можно представить в виде действия матрицы:
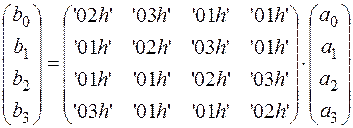 .
.
Матрица коэффициентов невырождена над 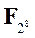 , поэтому операция обратима, а обратимое к ней действие реализуется матрицей, обратной к выписанной.
, поэтому операция обратима, а обратимое к ней действие реализуется матрицей, обратной к выписанной.
AddRoundKey. Сложение с подключом осуществляется побайтово по модулю 2 для каждого байта матрицы состояний с соответствующим элементом матрицы подключа. обратная операция, очевидно, совпадает с исходной.
Структура раундов.
Шифрование в алгоритме AES запишется в псевдокоде следующим образом:
AddRoundKey(S,K[0]);
For i:= 1 to 9 do Begin SubBytes(S); ShiftRows(S); MixColumns(S); AddRoundKey(S,K[i]) End;
SubBytes(S);
ShiftRows(S);
AddRoundKey(S,K[10])
Блок открытого текста, предназначенный для шифрования, записывается в виде матрицы состояний S. Полученный в результате алгоритма шифротекст представляется той же матрицей. В последнем раунде операция MixColumns не осуществляется.
Процедура расшифрования в псевдокоде:
AddRoundKey(S,K[10]);
§
Регистр сдвига с обратной связью состоит из двух частей: регистра сдвига и функции обратной связи.

Рис 19. Регистр сдвига с обратной связью.
В общем случае регистр сдвига представляет собой последовательность некоторых элементов кольца или поля. Наиболее часто применяются битовые регистры сдвига. Длина такого регистра выражается числом битов. При каждом извлечении бита все биты регистра сдвигаются вправо на одну позицию. Новый старший бит рассчитывается как функция всех остальных битов регистра. Выходом обычно является младший значащий бит. Периодом регистра сдвига называют длину выходной последовательности до начала ее повторения.
Простейший тип регистров сдвига – регистр сдвига с линейной обратной связью (РСЛОС или ЛРС). Обратная связь – простая операция XOR над некоторыми битами регистра. Перечень этих битов определяется характеристическим многочленом и называется последовательностью отводов. Иногда такую схему называют конфигурацией Фибоначчи.
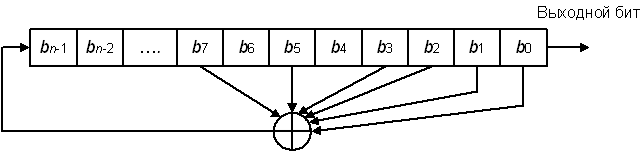
Рис.20. РСЛОС конфигурации Фибоначчи.
При программной реализации РСЛОС пользуются модифицированной схемой: для генерации нового значащего бита вместо использования битов последовательности отводов над каждым ее битом выполняется операция XOR с выходом генератора, заменяя старый бит последовательности отводов. Такую модификацию иногда называют конфигурацией Галуа.

Рис.21. РСЛОС конфигурации Галуа.
n-битовый РСЛОС может находиться в одном из 2n – 1 внутренних состояний. Это значит, что теоретически такой регистр может генерировать псевдослучайную последовательность с периодом 2n – 1 битов (заполнение нулями совершенно бесполезно). Прохождение всех 2n – 1 внутренних состояний возможно только при определенных последовательностях отводов. Такие регистры называют РСЛОС с максимальным периодом. Для обеспечения максимального периода РСЛОС необходимо, чтобы его характеристический многочлен был примитивным по модулю 2. Степень многочлена является длиной регистра сдвига. Примитивный многочлен степени n – это такой неприводимый многочлен, который является делителем 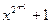 , но не является делителем xd 1 для всех d, являющихся делителями 2n – 1. (При обсуждении многочленов термин простое число заменяется термином неприводимый многочлен). Характеристический многочлен приведенных на рисунках РСЛОС:
, но не является делителем xd 1 для всех d, являющихся делителями 2n – 1. (При обсуждении многочленов термин простое число заменяется термином неприводимый многочлен). Характеристический многочлен приведенных на рисунках РСЛОС:
x32 x7 x5 x3 x2 x 1
примитивен по модулю 2. Период такого регистра будет максимальным, циклически проходя все 232 – 1 значений до их повторения. Наиболее часто используются прореженные многочлены, т.е. у которых есть только некоторые коэффициенты. наиболее популярны трехчлены.
Важным параметром генератора на базе РСЛОС, является линейная сложность. Она определяется как длина n самого короткого РСЛОС, который может имитировать выход генератора. Линейная сложность важна, поскольку при помощи простого алгоритма Берленкемпа-Мэсси можно воссоздать такой РСЛОС, проверив всего 2n битов гаммы. С определением нужного РСЛОС поточный шифр фактически взламывается.
Помимо РСЛОС применяются и регистры сдвига с нелинейной обратной связью, обратной связью по переносу и пр.
Ряд генераторов разработан на основе теоретико-числового подхода (генераторы Блюма-Микали, RSA, BBS, сжимающие, аддитивные генераторы и пр.).
Математическое обеспечение синтеза поточных криптографических алгоритмов разработано более полно и подробно по сравнению с блочными криптоалгоритмами. Тем не менее для создания поточных шифров зачастую используют блочные криптоалгоритмы в режимах OFB или CFB.
§
Пусть P – некоторое поле, e – единица поля P. Обозначим через 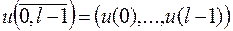 начальный отрезок произвольной последовательности u элементов поля P. Будем говорить, что многочлен
начальный отрезок произвольной последовательности u элементов поля P. Будем говорить, что многочлен
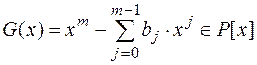
вырабатывает отрезок 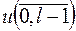 , если
, если
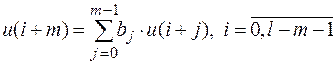 ,
,
то есть данный отрезок последовательности является отрезком некоторой линейной рекуррентной последовательности с характеристическим многочленом G(x). Алгоритм Берленкемпа-Месси строит многочлен G(x) наименьшей степени, вырабатывающий отрезок 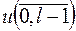 .
.
Определим функцию умножения последовательности на многочлен. Для произвольного многочлена 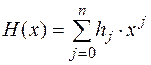 и последовательности v положим H(x) · v = w, где
и последовательности v положим H(x) · v = w, где
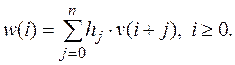
Многочлен G(x) вырабатывает l ³ m знаков последовательности u, если выполняется равенство
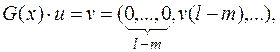
то есть если первые l – m знаков последовательности v равны нулю, а следующий за ними отличен от нуля.
Для многочлена G(x) Î P[x] степени m и последовательности u введем параметры lu(G) и ku(G) = lu(G) – m Î N È {0, ¥}, где lu(G) – число знаков последовательности u, вырабатываемых многочленом G(x). Ясно, что ku(G) – максимальное число первых подряд идущих нулей в последовательности G(x) · u (либо ¥).
Будем индуктивно строить последовательность многочленов G0(x), G1(x), … неубывающих степеней 0 = m0 < m1 £ m2 £ … .
Начальные условия: G0(x) = e, m0 = 0.
Этап 1. Если
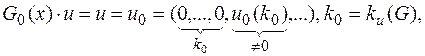
то полагаем
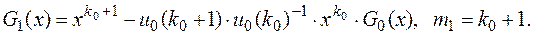
Если G1(x)·u = 0, то есть если ku(G1) = ¥, то G1(x) – искомый минимальный многочлен ЛРП u. В противном случае строим G2(x).
Этап t 1. пусть многочлены G0(x), …, Gt(x) уже построены, и степень многочлена Gj(x) равна mj, причем 0 = m0 < m1 £ m2 £ … mt. Пусть выполняются соотношения
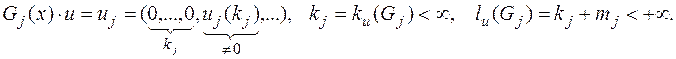 Определим число s = s(t) так, чтобы выполнялись условия mt = mt – 1 = … = ms 1 > ms (такое s найдется, так как m1 > m0). Положим
Определим число s = s(t) так, чтобы выполнялись условия mt = mt – 1 = … = ms 1 > ms (такое s найдется, так как m1 > m0). Положим
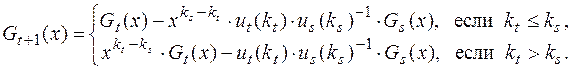
Если Gt 1(x)·u = 0, то нужный многочлен построен. В противном случае строим Gt 2(x).
Теорема:Если u – линейная рекуррентная последовательность над полем P с минимальным многочленом степени m, то F(x) = Gt(x) для некоторого подходящего значения t £ 2m – 1 – k0.
§
Не смотря на достаточно большой период и хорошие статистические качества, линейные рекуррентные последовательности имеют простое строение (ярко выраженная аналитическая связь между предыдущими и последующим элементами последовательности). Поэтому в криптографических приложениях используют различные способы усложнения аналитического строения линейных рекуррент.
Основной подход, применяемый при проектировании генератора гаммы на базе РСЛОС прост. Сначала берется один или несколько РСЛОС, обычно с различными длинами и различными характеристическими многочленами. (Если длины взаимно просты, а все многочлены обратной связи примитивны, то у сконструированного генератора будет максимальный период). Ключ является начальным состоянием регистров. Выходной бит представляет собой функцию, желательно нелинейную, некоторых битов РСЛОС.
Если выходной бит является функцией единственного РСЛОС, то генератор называется фильтрующим генератором.

Рис.22. Фильтрующий генератор.
Если выходной бит является функцией нескольких РСЛОС, то генератор называется комбинирующим генератором.
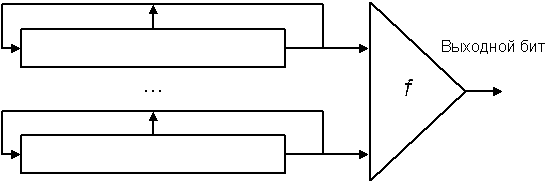
Рис.23. Комбинирующий генератор.
Еще один тип генераторов представляет собой композицию РСЛОС. В данной схеме выход одного из регистров подается на вход другого регистра.
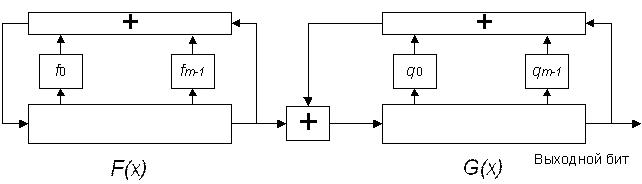
Рис.24. Генератор на основе композиции регистров сдвига..
Кроме перечисленных схем усложнения применяются и другие схемы (с динамическим изменением закона рекурсии с элементами памяти и пр.).
§
§
Для решения разнообразных криптографических задач блочные шифры используют в нескольких режимах работы. Рассмотрим этот вопрос на примере шифра DES.
Алгоритм DES может использоваться в следующих четырех режимах:
—режим электронной кодовой книги (ЕСВ — Electronic Code Book);
—режим сцепления блоков (СВС — Cipher Block Chaining);
— режим обратной связи по шифртексту (CFB — Cipher Feed Back);
—режим обратной связи по выходу (OFB — Output Feed Back).
Режим электронной кодовой книги (ЕСВ) отвечает обычному использованию DES как блочного шифра, осуществляющего некоторую простую замену блоков открытого текста. В режиме сцепления блоков (СВС) каждый блок Ci, i>1, шифртекста перед очередным зашифрованием складывается по модулю 2 со следующим блоком открытого текста Мi . При этом вектор С0 полагается равным начальному вектору IV (Initial Vector). Начальный вектор меняется ежедневно и хранится в секрете. Блоки С,,С2,… вырабатываются по рекуррентной формуле
Сi = DESk(Ci-1 Å Mi).
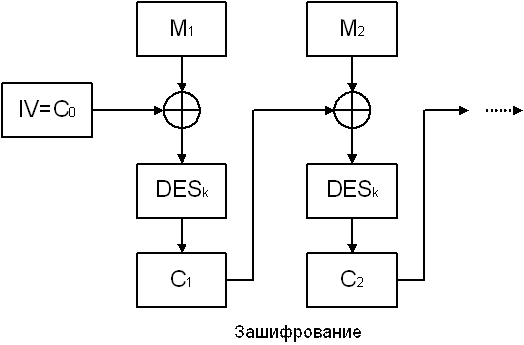
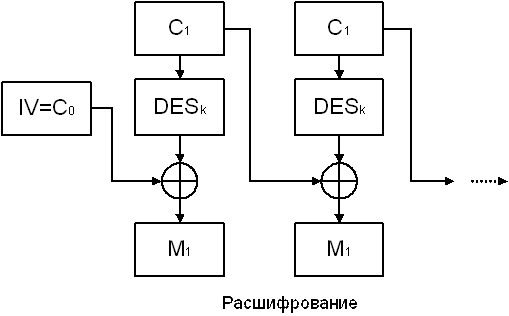
Рис.27. Режим CBC.
В режимах CFB и OFB алгоритм DES функционирует по аналогии с “шифром Вернама”, в режиме OFB — как синхронный шифр, в режиме CFB — как шифр с самосинхронизацией.
В режиме CFB вырабатывается блочная “гамма” Z0,Z1,…, причем Z0 полагается равным начальному вектору IV, а при i ≥ 1 блоки гаммы удовлетворяют соотношению Zi = DESk(Ci-1). Блоки открытого текста шифруются по правилу Ci = MiÅ Zi, i ≥ 1.
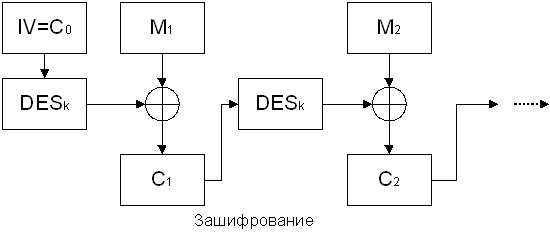
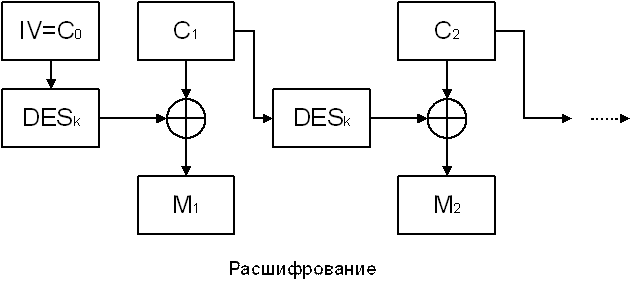
Рис.28. Режим CFB.
В режиме OFB вырабатывается блочная “гамма” Z0,Z1, …, причем Z0 полагается равным начальному вектору IV, а при i ≥ 1 блоки гаммы удовлетворяют соотношению Zi = DESk(Zi-1). Блоки открытого текста шифруются по правилу Ci=Mi Å Zi, i ≥ 1.
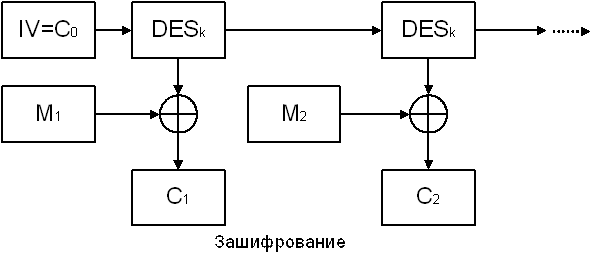
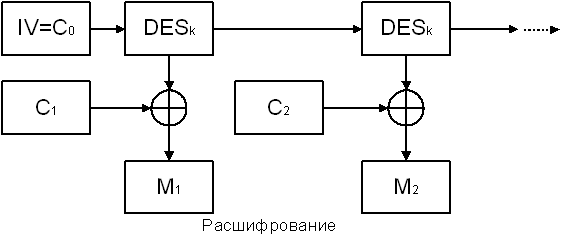 Рис.29. Рис.29. Режим OFB.
Рис.29. Рис.29. Режим OFB.
Кроме перечисленных режимов, DES имеет также “режим т-битовой обратной связи”, 1 ≤ т ≤ 64 . Этот режим оперирует с m-битовыми блоками. Входной блок (64-битовый регистр сдвига) вначале содержит вектор инициализации IV, “выровненный по правому краю”.
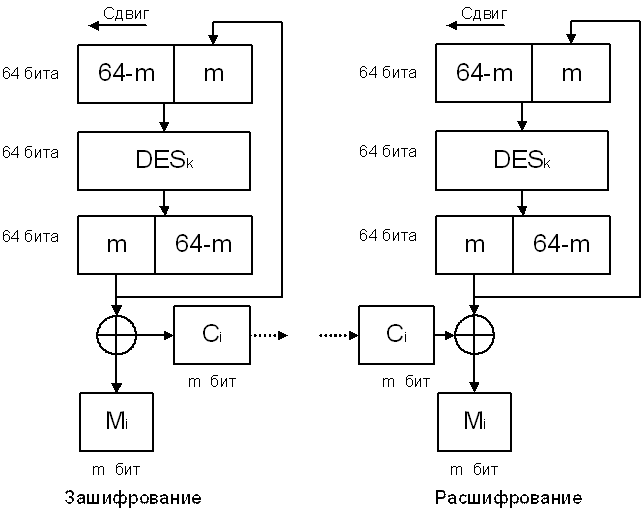
Рис.30. Режим m-битовой обратной связи.
Блоки открытого текста шифруются по правилу Сi= MiÅ Pi, где Pi— вектор, состоящий из т старших битов блока DESk(Сi-1). Обновление заполнения регистра сдвига осуществляется путем отбрасывания старших т битов и дописывания справа вектора Pi.
Указанные режимы имеют свои достоинства и недостатки. Основное достоинство режима ЕСВ — простота реализации. Недостаток — в возможности проведения криптоанализа “со словарем “. Дело в том что вследствие большой избыточности в открытом тексте вполне возможны повторения 64-битовых блоков. Это приводит к тому, что одинаковые блоки открытого текста будут представлены идентичными блоками шифртекста, что дает криптоаналитику возможность при наличии достаточно большого числа пар открытого и шифрованного текста восстанавливать с большой вероятностью блоки открытого текста по шифртексту.
В режимах ЕСВ и OFB искажение при передаче одного 64-битового блока шифртекста С, приводит к искажению после расшифрования соответствующего блока Miоткрытого текста, но не влияет на следующие блоки. Это свойство используется для шифрования информации, предназначенной для передачи по каналам связи с большим числом искажений. Вместе с тем при использовании режима OFB остается открытым вопрос о периоде получаемой выходной гаммы, который в некоторых предположениях может составлять величину порядка 232.
В режимах СВС и CFB искажение при передаче одного блока шифртекста Сi приводит к искажению на приеме не более двух блоков открытого текста — Мi, Mj 1. В то же время изменение блока Miприводит к тому, что Ciи все последующие блоки шифртекста будут искажены. Это свойство оказывается полезным для целей аутентификации. Такие режимы применяются для выработки кода аутентификации сообщения. Так, в режиме СВС берется вектор инициализации, состоящий из одних нулей. Затем с помощью ключа k вырабатываются блоки Ci,…,Cnшифртекста. Кодом аутентификации сообщения (КАС) служит блок Сп.
Если требуется обеспечить лишь целостность сообщения, отправитель передает блоки М1,…,Мпвместе с Сп. Тогда противнику, желающему изменить сообщение, нужно соответствующим образом изменить и блок Сп. Возможность этого маловероятна, если только противник не располагает секретным ключом k.
Если же нужно обеспечить шифрование и аутентификацию, то отправитель сначала использует ключ k1для выработки КАС, затем шифрует последовательность блоков М1,…,Мп, Мп 1 = КАС на втором ключе k2, и получает последовательность блоков С1,…,Сn,Сn 1. Получатель должен сначала расшифровать С1,…,Сп,Сп 1на ключе k2, а затем проверить (с помощью k ), что Мп 1— это КАС для М0, … , Мn.
Можно поступить и иначе: сначала использовать k для зашифрования М1,…, Мn, получая С1,…, Сn, а затем k2— для получения КАС. Получатель же будет использовать k2 для проверки КАС, а затем k — для расшифрования C1, .. ,Cn.
Во всех перечисленных режимах вместо алгоритма DES может быть использован любой алгоритм блочного шифрования, в частности российский стандарт ГОСТ 28147-89.
В российском стандарте также предусмотрено несколько режимов использования: режим простой замены, режим шифрования с обратной связью и режим гаммирования с обратной связью, которые являются аналогами соответственно режимов ЕСВ, СВС и CFB. Для того чтобы избавиться от указанной выше проблемы неопределенности длины периода гаммы в режиме OFB, в российском стандарте введен режим гаммирования, при котором блочный шифр используется в качестве узла усложнения некоторой последовательности гарантированного периода. Для выработки этой последовательности обычно применяются линейные регистры сдвига или счетчики по некоторому модулю.
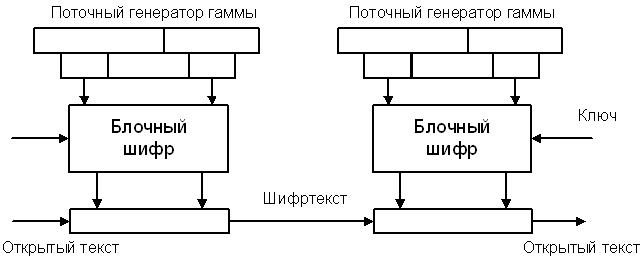
Рис.31. Режим гаммирования.
Уравнение шифрования имеет вид
Ci = Mi.Å F(γi), i = 1,2,…,
где F — преобразование, осуществляемое блочным шифром, γi– блоки, сформированные узлом выработки исходной гаммы из начального вектора γ1, который передается в начале сообщения в открытом или зашифрованном виде.
Ошибка при передаче, состоящая в искажении символа, приводит при расшифровании к искажению только одного блока, поэтому сохраняются все преимущества шифра гаммирования.
Контрольные вопросы
1. В чем различие между поточными и блочными шифрами?
2. Какие шифры удобнее в программной, а какие в аппаратной реализации?
3. Какие требования предъявляются к шифрующим преобразованиям блочных шифров?
4. В чем суть рассеивающих и перемешивающих преобразований при блочном шифровании?
5. Назовите основные параметры блочных шифров.
6. Какие виды поточных шифров могут быть эффективно реализованы программно?
7. Какие требования предъявляются к генераторам псевдослучайной последовательности?
8. Какие требования предъявляются к функции шифрования поточного шифра?
9. Какие режимы шифрования не распространяют искажений?
§
4.1. Математические основы асимметричной криптографии.
4.1.1. Свойства операций, определенных на некотором множестве
4.1.2. Функция Эйлера. Поле. Теоремы Эйлера – Лагранжа и Ферма.
4.1.3. Конечные поля.
4.1.4. Основные алгоритмы.
4.1.5. Алгоритмы нахождения НОД и мультипликативного обратного по модулю.
4.1.6. Китайская теорема об остатках.
4.1.7. Символы Лежандра и Якоби. Извлечение корней.
4.2. Примеры современных асимметричных шифров.
4.2.1. Криптосистема RSA.
4.2.2. Взаимосвязь компонентов RSA.
4.2.3. Криптосистема Эль-Гамаля.
4.2.4. Криптосистема Рабина.
4.2.5. Рюкзачные криптосистемы.
4.2.6. Шифрсистема Мак-Элиса.
Математические основы асимметричной криптографии.
Преимущество систем с открытым ключом состоит в том, что ключ не требуется сохранять в тайне. Необходимо лишь обеспечить его аутентичность, что сделать, как правило, легче, чем обеспечить рассылку секретных ключей.
Системы шифрования с открытым ключом осуществляют блочное шифрование, поэтому открытый текст перед шифрованием разбивается на блоки.
Ассиметричные системы шифрования обеспечивают значительно меньшие скорости шифрования, нежели симметричные, в силу чего они обычно используются не для шифрования сообщений, а для шифрования пересылаемых сеансовых секретных ключей, которые затем используются в симметричных системах шифрования.
Для понимания принципов построения асимметричных криптосистем необходимо повторить некоторые понятия алгебры и алгоритмы теории чисел.
Свойства операций.
Рассмотрим основные свойства арифметических операций определенных на некотором множестве А.
*, 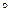 – обозначение операций.
– обозначение операций.
Замкнутость: 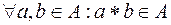
Ассоциативность: 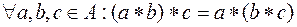
Наличие нейтрального элемента Q Î A: 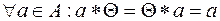
Существование обратного элемента 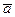 Î A:
Î A: 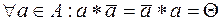
Коммутативность: 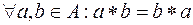
Дистрибутивность операции 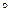 относительно операции *:
относительно операции *: 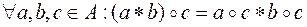
Группы, кольца.
Определение. Группа – множество G с операцией, которая: замкнута, обладает нейтральным элементом, ассоциативна, относительно нее каждый элемент обладает обратным. Группу с коммутативной операцией называют коммутативной или абелевой.
Практически все группы в криптографии – абелевы. Обозначение группы: (G, знак операции).
Мультипликативная группа (G, · ):
Групповая операция – умножение · ;
Нейтральный элемент – единица 1 ;
Обратный элемент – a-1;
Многократное применение операции – возведение в степень
a5 = a · a · a · a · a.
Аддитивная группа (G, ):
Групповая операция – сложение ;
Нейтральный элемент – ноль 0 ;
Обратный элемент – – a;
Многократное применение операции – умножение
5 · a = a a a a a.
Образующая g – такой элемент группы, что любой другой элемент может быть получен путем многократного применения к нему групповой операции. Запись 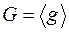 .
.
В мультипликативной группе: 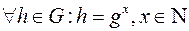
В аддитивной группе: 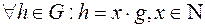
Определение. Кольцо – множество R с двумя операциями: сложением и умножением, в котором обе операции замкнуты, ассоциативны, обладают нейтральным элементом, связаны законом дистрибутивности, а сложение коммутативно и для каждого элемента есть обратный по сложению. Обозначение кольца (R, ·, ).
В коммутативном кольце операция умножения дополнительно обладает свойством коммутативности.
Основное кольцо, важное для криптологии – коммутативное кольцо остатков от деления на натуральное число n, большее 1, которое также называют кольцом вычетов по модулю n и обозначают Zn или Z/nZ.
§
Одна из центральных задач арифметики остатков – решение сравнения:
a · x º b (mod n)
– Если НОД (a, n) = 1, то существует ровно одно решение, и оно находится с помощью a-1: так как
a · a-1 º 1 (mod n),
то, домножив обе части сравнения на a-1, получим
x º b · a-1 (mod n).
– Если НОД (a, n) = g ¹ 1 и g | b, то сравнение имеет g решений. Чтобы их найти нужно разделить исходное сравнение на g:
a’ · x’ º b’ (mod n’),
где a’ = a / g, b’ = b / g, n’ = n / g. Если x’ – решение полученного сравнения, то решение исходного сравнения – любое число вида
x = x’ i · n’,
где i = 0, 1, …, g – 1.
– В других случаях решений нет.
Пример:
7 · x º 3 (mod 143) – одно решение,
11 · x º 3 (mod 143) – решений нет,
11 · x º 22 (mod 143) – 11 решений.
Ситуация с единственным решением наиболее интересна для криптологии, поэтому важно знать количество элементов кольца, взаимно простых с его модулем. Оно дается функцией Эйлераj и равно j(n). Значение j(n) можно легко найти по разложению числа n на простые множители. Если
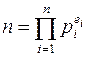 ,
,
где pi – различные простые числа, то
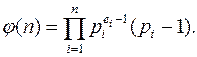
Функция Эйлера для любого n > 2 имеет четное значение.
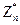 – наибольшее подмножество элементов, образующих группу по умножению #
– наибольшее подмножество элементов, образующих группу по умножению # 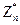 = j(n). (количество элементов мультипликативной группы кольца вычетов по модулю n равно j(n)).
= j(n). (количество элементов мультипликативной группы кольца вычетов по модулю n равно j(n)).
Особый интерес представляют частные случаи:
1. Если p простое, то j(p) = p – 1.
2. Если p и q – простые и p ¹ q, то j(p · q) = (p – 1)(q – 1).
Если p – простое число, то любой элемент в Zp(или Z/pZ) обладает мультипликативным обратным. Кольца с такими свойствами называются полями.
Определение. Полем называется множество (F, ·, ) с двумя операциями, обладающее свойствами:
– (F, ) – абелева группа с нейтральным элементом 0,
– (F {0}, ·) – абелева группа с нейтральным элементом 1,
– (F, ·, ) удовлетворяет закону дистрибутивности (умножение дистрибутивно относительно сложения).
Поле – коммутативное кольцо, в котором каждый ненулевой элемент обратим. Каждый ненулевой элемент кольца Zp взаимно прост с p, так как p простое и, следовательно, обратим. Значит Zp – конечное поле, которое обычно называют полем вычетов по модулю p и обозначают Fp = {0, 1, …, p – 1}. Мультипликативная группа 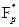 = {1, …, p – 1} поля вычетов содержит все ненулевые элементы Fp.
= {1, …, p – 1} поля вычетов содержит все ненулевые элементы Fp.
Теорема Лагранжа.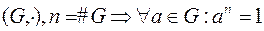 .
.
Обобщение Эйлера для малой теоремы Ферма.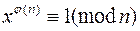 , при НОД(x, n) = 1.
, при НОД(x, n) = 1.
Малая теорема Ферма.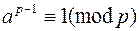 .
.
Конечные поля.
Целые числа по простому модулю – не единственный пример конечных полей. Более общий тип полей используется при рассмотрении таких криптосистем как AES, поточных шифров на основе РСЛОС и криптосистем, на основе эллиптических кривых.
Рассмотрим множество многочленов от переменной x с коэффициентами из Fp. Это множество обозначается через Fp[x] и образует кольцо относительно естественных операций суммы и умножения многочленов. Особый интерес представляет случай p = 2.
Пример. В кольце F2[x] выполнены равенства:
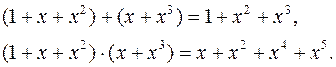
Зафиксируем многочлен f(x) и будем рассматривать остальные элементы кольца Fp[x] по модулю f(x). Как и натуральные числа по модулю n, возможные остатки от деления на многочлен f(x), будут образовывать кольцо. Оно обозначается через Fp[x]/f(x)Fp[x] (по аналогии с Z/nZ).
Пример.f(x) = x4 1 и p = 2. Тогда
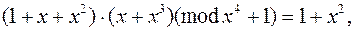
так как

По аналогии с целыми числами по модулю n, где рассматривалось сравнение
a · x º b (mod n)
можно поставить аналогичный вопрос и для многочленов. Пусть a, b и f – многочлены из Fp[x]. Существование решения уравнения
a · a º b (mod f)
также зависит от НОД (a, f) и также возможны три ситуации. Наиболее интересна ситуация, когда НОД (a, f) = 1.
Многочлен называется неприводимым, если у него нет делителей, отличных от него самого и констант. Неприводимость многочленов – то же самое, что и простота целых чисел. Кольцо Fp[x]/f(x)Fp[x] является конечным полем тогда и только тогда, когда многочлен f(x) неприводим.
Рассмотрим два неприводимых многочлена над полем F2
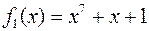 и
и 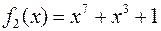 .
.
Возникают два конечных поля
F1 = Fp[x]/f1(x)Fp[x] и F2 = Fp[x]/f2(x)Fp[x],
каждое состоит из 27 двоичных многочленов (каждый имеет ровно 7 коэффициентов равных 1 или 0), степень которых не превосходит 6. Сложение в обоих полях выглядит одинаково, поскольку при вычислении суммы складываются коэффициенты многочленов по модулю 2. А вот умножаются элементы этих полей по разному:
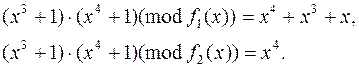
Действительно ли различны поля F1 и F2 или это только кажущееся различие?
Изоморфны ли поля F1 и F2?
Изоморфизм: отображение j: F1 ® F2, удовлетворяющее двум требованиям:
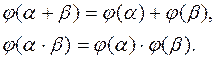
Для построения изоморфизма между F1 и F2 достаточно показать как выражается корень f2(x) в виде многочлена от корня f1(x).
Изоморфизм существует между любыми двумя конечными полями с одинаковым числом элементов. Все конечные поля совпадают либо с целыми числами по простому модулю, либо с многочленами по модулю неприводимого многочлена.
Теорема. Существует единственное (с точностью до изоморфизма) конечное поле с числом элементов равным степени простого числа.
Конечное поле из q = pd элементов обозначается символом Fq или GF(q) (поле Галуа из q элементов).
Любое конечное поле K содержит в себе экземпляр поля целых чисел по некоторому простому модулю p, который называется простым подполем поля K. Число элементов простого подполя называется характеристикой поля и обозначается через char K. В частности char Fp = p. На конечном поле характеристики p можно определить отображение Фробениуса:
Ф: Fq®Fq, Ф(a) = (ap)
которое является автоморфизмом (изоморфизмом поля с самим собой). Множество элементов из Fq, остающихся неподвижными при действии Ф, совпадает с его простым подполем:
{a Î Fq| ap = a} = Fp.
Это утверждение – обобщение малой теоремы Ферма на случай любых конечных полей.
Ненулевые элементы конечного поля составляют конечную абелеву циклическую группу 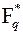 . Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, их может быть и несколько. Всегда можно найти такой элемент g Î Fq, что любой ненулевой элемент a Î Fq будет представляться в виде
. Образующая этой группы называется примитивным элементом конечного поля. Примитивный элемент есть в любом конечном поле, их может быть и несколько. Всегда можно найти такой элемент g Î Fq, что любой ненулевой элемент a Î Fq будет представляться в виде
a = gx
при некотором целом показателе x.
Пример. В поле из восьми многочленов
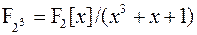 .
.
В нем существует 7 ненулевых элементов, а именно
1, a, a 1, a2, a2 1, a2 a, a2 a 1,
где a – корень многочлена x3 x 1 (искусственно введенный элемент, удовлетворяющий соотношению a3 a 1 = 0, в котором все действия выполняются по модулю 2).
Тогда:
a1 = a,
a2 = a2,
a3 = a 1,
a4 = a2 a,
a5 = a2 1,
a6 = a2 a 1,
a7 = 1
и a – примитивный элемент поля 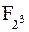 . Целые числа по модулю p также имеют примитивный элемент, так как Fp – конечное поле.
. Целые числа по модулю p также имеют примитивный элемент, так как Fp – конечное поле.
§
Алгоритм А (Разложение на простые множители путем деления). По данному положительному целому числу N этот алгоритм находит простые множители p1 ≤ р2 ≤ … ≤ pt числа N. В этом методе используется вспомогательная последовательность пробных делителей
d = d0 < d1 < d2 < d3 < …,
которая включает в себя все простые числа < 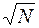 (и, если это удобно, может содержать числа, не являющиеся простыми). Последовательность чисел di должна также содержать по крайней мере одно значение, такое, что dk >
(и, если это удобно, может содержать числа, не являющиеся простыми). Последовательность чисел di должна также содержать по крайней мере одно значение, такое, что dk > 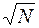 .
.
А1. [Начальная установка.] Присвоить t ← 0, k ← 0, n ← N. (В ходе выполнения алгоритма переменные t, k, n подчинены следующим условиям: “n = N/p1…pt и n не имеет простых множителей, меньших dk“.)
А2. [n = 1?] Если n = 1, алгоритм заканчивается.
A3. [Разделить.] Присвоить q ← 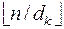 , r ← n mod dk. (Здесь q и r – соответственно частное и остаток от деления числа n на dk.)
, r ← n mod dk. (Здесь q и r – соответственно частное и остаток от деления числа n на dk.)
А4. [Остаток равен нулю?] Если r ≠ 0, то перейти к шагу А6.
А5. [Множитель найден.] Увеличить t на 1 и присвоить pt ← dk, n ← q. Возвратиться к шагу А2.
А6. [Частное мало?] Если q > dk, увеличить k на 1 и возвратиться к шагу A3.
А7. [n — простое число.] Увеличить t на 1, присвоить pt ← n и завершить выполнение алгоритма.
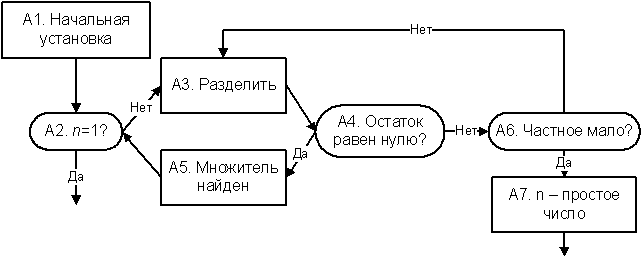
Рис.32. Алгоритм разложения числа на простые множители.
Пример.
Разложение на простые множители числа N = 25852. Сразу же находим, что N = 2 · 12926; следовательно, р1 = 2. Далее, 12926 = 2 · 6463, так что р2 = 1. Но теперь число n = 6463 не делится на числа 2, 3, 5, …, 19; находим, что n = 23 · 281; значит, р3 — 23. В итоге имеем 281 = 12 · 23 5 и 12 ≤ 23, т. е. р4 = 281.
Алгоритм Евклида.
Разделить целое число a на число b с остатком – это значит найти такие числа q и r c 0 £ r < |b|, при которых выполняется равенство
a = q · b r.
Разделить многочлен f на многочлен g с остатком – это значит найти такие многочлены q и r c 0 £ deg r < deg g, при которых выполняется равенство
f = q · g r.
Для вычисления НОД(r0 = a, r1 = b) производится деление с остатком по следующей схеме:
a = r0 = q1r1 r2,
b = r1 = q2r2 r3,
…..
rm-2 = qm-1bm-1 rm,
rm-1 = qmrm.
Работа алгоритма Евклида основана на том, что отображение 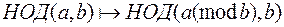 сохраняет наибольший общий делитель.
сохраняет наибольший общий делитель.
Отображение работает до a = НОД, b = 0.
Пример.
НОД(21, 12) = НОД (21 (mod 12), 12) =
= НОД(12, 9) = НОД (12 (mod 9), 9) =
= НОД(9, 3) = НОД (9 (mod 3), 3) =
= НОД(3, 0) = 3
Работа бинарного алгоритма нахождения НОД основана на следующем ряде отображений, также сохраняющих НОД:
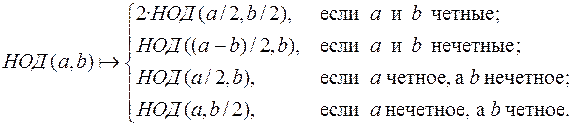
Отображения работают до (a – b) /2 = 0. НОД = b.
Пример.
НОД(21, 12) = НОД (21, 12 / 2) =
= НОД(21, 6) = НОД (21, 6 / 2) =
= НОД(21, 3) = НОД ((21 – 3) / 2, 3) =
= НОД(9, 3) = НОД ((9 – 3) / 2, 3) =
= НОД(3, 3) = НОД ((3 – 3) / 2, 3) =
= НОД(0, 3) = 3
Во всех вышеперечисленных рассуждениях принимается a ³ b.
§
Алгоритм Евклида.
Алгоритм А. (Алгоритм Евклида в современной редакции). По данным неотрицательным целым числам u и v этот алгоритм находит их наибольший общий делитель.
A1. [v = 0?] Если v = 0, то выполнение алгоритма заканчивается, а в качестве результата возвращается число u.
A2. [Взять u mod v.] Присвоить r u mod v, u v, v r и вернуться к шагу A1. (В результате выполняемых на этом шаге операций значение v уменьшается, значение НОД(u, v) остается неизменным.)
Бинарный алгоритм НОД.
Алгоритм B. (Бинарный алгоритм нахождения наибольшего общего делителя). По данным неотрицательным целым числам u и v этот алгоритм находит их наибольший общий делитель. (Использует знаковое представление чисел).
B1. [Найти степень 2.] Присвоить k 0, затем повторно присваивать kk 1, u u / 2, v v / 2 нуль или более раз до тех пор, пока одно или оба числа u и v станут нечетными.
B2. [Начальная установка.] (Исходные значения чисел u и v уже разделены на 2k, и по крайней мере одно из текущих значений нечетно.) Если нечетно u, то присвоить t – v и перейти к шагу B4. В противном случае присвоить tu.
B3. [Уменьшить t наполовину.] (Здесь t четно и не нуль.) Присвоить tt / 2.
B4. [t четно?] Если t четно, то вернуться к шагу B3.
В5. [Установить max(u, v) заново.] Если t > 0, то присвоить u t, в противном случае присвоить v – t. (Большее из чисел u и v заменяется на |t| за исключением, возможно, первого выполнения этого шага.)
B6. [Вычесть.] Присвоить t u – v. Если t ¹ 0, то вернуться к шагу B3. В противном случае алгоритм останавливает выполнение, а на выходе будет u · 2k.

Рис.33. Бинарный алгоритм НОД.
Расширенный алгоритм Евклида.
Алгоритм X. (Обобщенный алгоритм Евклида). Для заданных целых чисел u и v этот алгоритм определяет вектор (u1, u2, u3), такой, что uu1 vu2 = u3 = НОД(u, v). В процессе вычисления используются вспомогательные векторы (v1, v2, v3), (t1, t2, t3); действия производятся таким образом, что в течение всего процесса вычисления выполняются соотношения
ut1 vt2 = t3 uu1 vu2 = u3 uv1 vv2 = v3.
X1. [Начальная установка.] Присвоить (u1, u2, u3) (1, 0, u), (v1, v2, v3) (0, 1, v).
X2. [v3 = 0?] Если v3 = 0, то выполнение алгоритма заканчивается.
X3. [Разделить и вычесть.] Присвоить 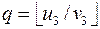 , затем присвоить
, затем присвоить
(t1, t2, t3) (u1, u2, u3) – (v1, v2, v3) · q,
(u1, u2, u3) (v1, v2, v3),
(v1, v2, v3) (t1, t2, t3).
Возвратиться к шагу X2.
Расширенный бинарный алгоритм НОД.
Алгоритм Y. Модификация алгоритма X с использованием принципов алгоритма B. Для заданных целых чисел u и v этот алгоритм определяет вектор (u1, u2, u3), такой, что uu1 vu2 = u3 = НОД(u, v). В процессе вычисления используются вспомогательные векторы (v1, v2, v3), (t1, t2, t3); в течение всего процесса вычисления так же, как и в X выполняются соотношения
ut1 vt2 = t3 uu1 vu2 = u3 uv1 vv2 = v3.
(Использует знаковое представление чисел).
Y1. [Найти степень 2.] То же, что в шаге B1.
Y2. [Начальная установка.] Присвоить (u1, u2, u3) (1, 0, u), (v1, v2, v3) (v, 1 – u, v). Если число u нечетно, присвоить (t1, t2, t3) (0, –1, –v) и прейти к шагу Y4. В противном случае присвоить (t1, t2, t3) (1, 0, u).
Y3. [Выполнить половинное деление t3.] Если t1 и t2 четны, присвоить (t1, t2, t3) (t1, t2, t3)/2; иначе присвоить (t1, t2, t3) (t1 v, t2 – u, t3)/2. (В последнем случае t1 v и t2 – u будут оба четными.)
Y4. [t3 четно?] Если t3 четно, вернуться к шагу Y3.
Y5. [Переустановить max(u3 v3).] Если t3 положительно, присвоить (u1, u2, u3) (t1, t2, t3); иначе присвоить (v1, v2, v3) (v – t1, – u – t2, – t3).
Y6. [Вычесть.] Присвоить (t1, t2, t3) (u1, u2, u3) – (v1, v2, v3). Затем, если t1 £ 0, присвоить (t1, t2) (t1 v –, t2 – u). Если t3 ¹ 0, вернуться к шагу Y3. В противном случае закончить выполнение алгоритма с результатом, равным (u1, u2, u3 · 2k).
§
Пусть p – простое число, большее 2. Рассмотрим отображение
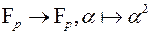 ,
,
сопоставляющее каждому элементу поля его квадрат. На множестве ненулевых элементов поля Fp это отображение в точности «два-в-один», то есть если из ненулевого элемента x Î Fp можно извлечь квадратный корень, то таких корней у него ровно 2 и, кроме того, ровно половина элементов из 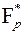 являются полными квадратами. Полные квадраты в
являются полными квадратами. Полные квадраты в 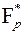 называются квадратичными вычетами по модулю p. Множество всех квадратичных вычетов по модулю p является подгруппой порядка (p – 1)/2 в мультипликативной группе
называются квадратичными вычетами по модулю p. Множество всех квадратичных вычетов по модулю p является подгруппой порядка (p – 1)/2 в мультипликативной группе 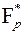 . Элементы мультипликативной группы
. Элементы мультипликативной группы 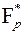 из которых нельзя извлечь квадратный корень, называются квадратичными невычетами.
из которых нельзя извлечь квадратный корень, называются квадратичными невычетами.
Для выявления полных квадратов по модулю p вводится символ Лежандра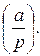
Он равен 0, если a делится на p, 1, если a – квадратичный вычет по модулю p, и – 1, если a – квадратичный невычет.
Символ Лежандра легко вычисляется по формуле
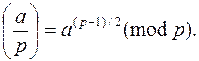
Но использование этой формулы сопряжено с вычислениями больших степеней и на практике предпочитают пользоваться законом квадратичной взаимности
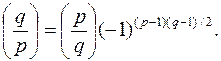
Иначе говоря
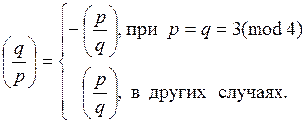
При вычислении символа Лежандра большую помощь оказывают следующие дополнительные формулы:
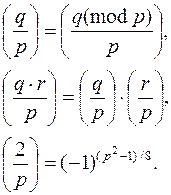
Пример. С использованием разложения на множители вычислим символ Лежандра.
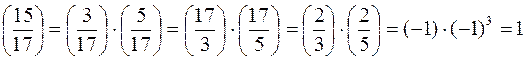
Извлечение квадратного корня из квадратичного вычета a по модулю p при помощи алгоритма Шенкса.
1. Выбрать наугад такое n, что 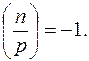
2. Пусть e, q – целые числа с нечетным q, удовлетворяющие соотношению p – 1 = 2eq.
3. Положим y = nq (mod p), r = e, x = a(q – 1)/2 (mod p).
4. Положим b = ax2 (mod p), x = ax (mod p).
5. Пока b ¹ 1 (mod p) делать:
· найти наименьшее число m, такое, что 
· положить 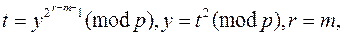
· положить 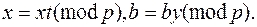
6. Вывести x.
Если p = 3 (mod 4), то для извлечения квадратного корня из a можно использовать формулу
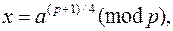
формула дает правильный ответ потому, что
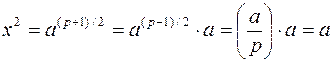 .
.
Символ Лежандра определен только в случае простого знаменателя. Если же знаменатель составной, то вводится символ Якоби, обобщающий символ Лежандра.
Пусть n – нечетное число, большее 2 и
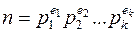 .
.
Символ Якоби определяется через символы Лежандра простых делителей числа n следующим образом
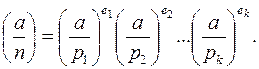
Символ Якоби можно вычислять так же, как и символ Лежандра, опираясь на тождество, выведенное из закона квадратичной взаимности:
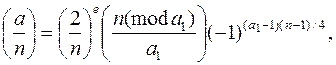
где a = 2ea1 и a1 нечетно. Полезно помнить еще несколько формул, справедливых при нечетном n:
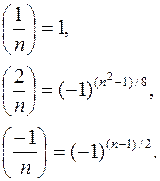
Это дает быстрый алгоритм вычисления символа Якоби и, соответственно, символа Лежандра, как его частный случай, без разложения на множители. Единственное, что нужно сделать – выделить максимальную степень двойки.
Пример.
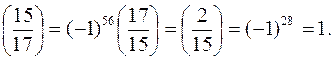
Символ Лежандра 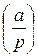 сообщает нам, является ли a полным квадратом по модулю простого числа p. Символ Якоби ничего не утверждает о возможности извлечения квадратного корня из a по модулю составного числа n. Если a в действительности квадрат по модулю n, то символ Якоби будет равен 1. Однако из равенства
сообщает нам, является ли a полным квадратом по модулю простого числа p. Символ Якоби ничего не утверждает о возможности извлечения квадратного корня из a по модулю составного числа n. Если a в действительности квадрат по модулю n, то символ Якоби будет равен 1. Однако из равенства 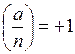 нельзя сделать вывод о том, что a – полный квадрат. Не смотря на благоприятное равенство, квадратный корень из a может не извлекаться.
нельзя сделать вывод о том, что a – полный квадрат. Не смотря на благоприятное равенство, квадратный корень из a может не извлекаться.
Извлечение корня из числа по модулю составного n = p · q в предположении, что разложение n на простые множители известно и a – полный квадрат по модулю n, то есть
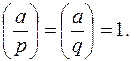
Сначала извлекается корень из a по модулю p и обозначается через sp (таких корней два, как будет показано позже). Затем извлекается квадратный корень из a по модулю q и обозначается sq (таких корней также два). Наконец, для вычисления искомого корня применяем китайскую теорему об остатках к системе
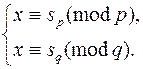
Пример. Вычислим корень из a = 217 по модулю n = 221 = 13 · 17.
Квадратные корни из a по модулям 13 и 17 соответственно равны s13 = 3 и s17 = 8. Опираясь на китайскую теорему об остатках, получаем s = 42. Проверим правильность данного решения: s2 = 422 ≡ 217 (mod 221).
Существуют еще три квадратных корня из a = 217 по модулю n = 221, поскольку n имеет два простых делителя. Для их отыскания применим КТО к трем системам с коэффициентами:
s13 = 10, s17 = 8;
s13 = 3, s17 = 9;
s13 = 10, s17 = 9
и получить полный ответ: 42, 94, 127, 179.
§
Криптосистема RSA.
Система построена на следующих функциях:
Односторонняя функция – умножение двух больших простых чисел:
N = p · q.
Обратная задача – задача факторизации, является сложной.
Односторонняя функция с секретом – потенцирование (возведение в степень) по модулю составного N = p · q сфиксированной степенью E:
C = mE mod N.
Обратная задача – задача извлечения корня степени E по модулю N:
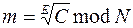
является сложной, если неизвестно разложение N на множители (секрет) и является простой при известном разложении N.
В дальнейшем секретные элементы криптосистем обозначаются строчными (p, q, m и пр.) открытые прописными (N, C, E и пр.) латинскими буквами.
Предположим абонент A считает нужным разрешить всем желающим отправлять ему секретные сообщения, расшифровать которые способен только он. Для этого выбирается два больших простых числа p и q, которые держатся в секрете, и публикуется их произведение
N = p · q,
которое называют модулем алгоритма. Кроме того, выбирается шифрующая экспонента E, удовлетворяющая условию
НОД (E, (p – 1), (q – 1)) = 1.
Как правило E берут равным 3, 17 или 65537. Пара, доступная всем желающим, – это (N, E). Для выбора секретного ключа применяют расширенный алгоритм Евклида к паре чисел E и
(p – 1)(q – 1), получая при этом расшифровывающую экспоненту d. Найденная экспонента удовлетворяет соотношению
E · d = 1 (mod (p – 1)(q – 1)) = 1.
Секретным ключом является тройка (d, p, q). Фактически, можно было бы выбросить простые делители p и q из ключа и помнить лишь о d и всем числе N. Но, как будет рассмотрено позднее, это снизит скорость алгоритма.
Допустим теперь пользователь B намерен зашифровать сообщение, адресованное A. Он сверяется с открытым ключом и представляет сообщение в виде числа m, строго меньшего модуля N алгоритма. Шифртекст C получается из m по следующему правилу:
C = mE (mod N).
A, получив шифрограмму, расшифровывает ее, возводя число C в степень d:
m = Cd (mod N).
Равенство имеет место в связи с тем, что порядок группы
#(Z/NZ)* = φ(N) = (p – 1)(q – 1).
Потому по теореме Лагранжа (Эйлера-Ферма),
x(p – 1)(q – 1) = 1 (mod N)
для любого числа x Î (Z/NZ)*. Поскольку E и d взаимно обратны по модулю (p – 1)(q – 1), при некотором целом числе s получается равенство
Ed – s(p – 1)(q – 1) = 1.
Следовательно,
Cd = (mE)d = mEd = m1 s(p – 1)(q – 1) = m · m s(p – 1)(q – 1) = m (mod N).
Пример. Пусть p = 7 и q = 11. Тогда N = 77, а (p – 1)(q – 1) = 6 · 10 = 60. В качестве открытой шифрующей экспоненты возьмем число E = 37, поскольку НОД(37, 60) = 1. Применяя расширенный алгоритм Евклида, найдем d = 13, так как
37 · 13 = 481 = 1 (mod 60).
Для зашифрования сообщения численное представление которого имеет вид m = 2:
C = mE (mod N) = 237 (mod 77) = 51.
Расшифрование происходит аналогично:
m = Cd (mod N) = 5113 (mod 77) = 2.
§
Задача RSA: Даны числа C и E, последнее из которых удовлетворяет соотношению:
НОД(E, (p – 1)(q – 1)) = 1.
Требуется найти такое число m, что
mE = C (mod N).
Лемма. Задача RSA не сложнее проблемы факторизации.
Доказательство. Применяя алгоритм факторизации, разложим число N на простые множители, вычислим значение функции Эйлера Ф = j(N) и найдем
D = 1/E (mod Ф).
Теперь, зная число D, легко восстановить m, поскольку
CD = mED = m1 (mod Ф) = m (mod N).
Отсюда следует, что при известных p и q легко находятся d и m.
Самые большие числа, которые к настоящему времени удается разложить на множители за разумное время, имеют 500 двоичных знаков. В связи с этим, для обеспечения стойкости систем среднего срока действия, рекомендуют брать модули шифрования порядка 1024 бит. Для систем большого срока действия следует выбирать модули, состоящие из 2048 бит.
Секретная экспонента и проблема факторизации:
Лемма. Если известна секретная экспонента d алгоритма RSA, соответствующая открытому ключу (N, E), то число N можно эффективно разложить на множители.
Доказательство. При некотором целом s имеет место равенство
Ed – s(p – 1)(q – 1) = 1.
Возьмем произвольное целое число X ¹ 0. Тогда
XEd – 1= 1(mod N).
Вычисляем квадратный корень Y1 по модулю N:
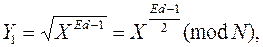
что можно сделать, поскольку Ed – 1 известно и четно. Приходим к тождеству
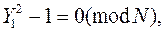
которое можно использовать для определения делителей числа N с помощью вычисления НОД(Y1 – 1, N). Однако это будет работать только если Y1 ¹ ±1 (mod N).
Предположим, что нам не повезло и Y1 = ±1 (mod N). Если Y1 = –1 (mod N), вернемся к началу и выберем другое число X. Если Y1 = 1 (mod N), то можно взять еще один квадратный корень
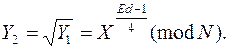
Опять получаем
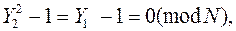
откуда НОД(Y2 – 1, N) – делитель числа N. К сожалению, здесь тоже может оказаться, что Y2 = ±1 (mod N). Тогда придется повторить все снова.
Алгоритм необходимо повторять до тех пор, пока мы не разложим N на множители и не придем к числу (ED – 1)/2t, которое уже не будет делиться на 2. В последнем случае придется вернуться к началу алгоритма, выбрать новое случайное значение X и все повторить.
Отсюда следует, что при известном d легко найти p и q.
Алгоритм, приведенный в доказательстве, – типичный пример алгоритма Лас-Вегаса, вероятностного по своей природе, которая проявляется в процессе работы. Но если уж ответ отыщется, то он будет обязательно верным.
Пример. Входные данные задачи RSA:
N = 1441499, E = 17 и d = 507905.
Напомним, что мы предполагаем известной расшифровывающую экспоненту d, которая обычно хранится в секрете. Опираясь на предыдущий алгоритм, найдем числа N. Положим
T1 = (Ed – 1)/2 = 4317192,
X = 2.
Для вычисления Y1, сделаем преобразования :
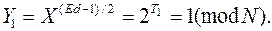
Поскольку Y1 оказался равным 1, нам нужно взять
T2 = T1/2 = (Ed – 1)/4 = 2158596 и 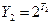 .
.
Теперь
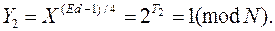
Снова нужно повторять предыдущие шаги, что приведет нас к
T3 = (Ed – 1)/8 = 1079298
и
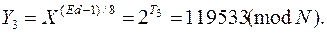
Отсюда
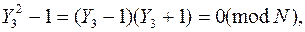
и мы можем найти простой делитель числа N, вычислив
НОД(Y3 – 1, N) = 1423.
Значение функции Эйлера j(N) и проблема факторизации:
Лемма. Значение Ф = j(N) позволяет эффективно разложить число N на множители.
Доказательство. Имеем
Ф = (p – 1)(q – 1) = N – (p q) 1.
Следовательно, положив S = N 1 – Ф, мы получим
S = p q.
Нам нужно определить числа p или q, опираясь на их сумму S и произведение N. Рассмотрим многочлен
f(X) = (X – p)(X – q) = X2 – SX N.
Теперь можно найти как p, так и q, решая квадратное уравнение f(X) = 0 стандартным образом:
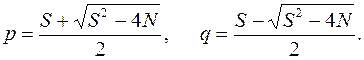
Отсюда следует, что при известном j(N) легко найти p и q.
Пример. Открытый модуль N = 18923 криптосистемы RSA. Известно Ф = j(N) = 18648. Вычисляем
S = p q = N 1 – Ф = 276.
Соответствующий многочлен имеет вид:
f(X) = X2 – SX N = X2 – 276X 18923,
а его корни – p = 149, q = 127.
§
Разделенный модуль: Поскольку арифметика остатков – дорогое удовольствие с точки зрения компьютера, весьма заманчиво разработать систему шифрования, в которой пользователи разделяют общий модуль N, но применяют различные открытые и закрытые экспоненты (Ei, di).
Одна из причин, побуждающая это делать, – ускорить алгоритмы зашифрования и расшифрования в аппаратных средствах, специально настроенных на определенный модуль N. Однако это неудачная идея, поскольку пасует перед двумя типами нападающих: внутреннего, то есть законного пользователя системы, и внешнего.
Предположим, что нападающим является один из законных клиентов криптосистемы, скажем пользователь номер 1. Он может найти значение секретной экспоненты пользователя 2 – d2. Сначала он вычисляет p и q по известному ему d1. Затем злоумышленник находит
j(N) = (p – 1)(q – 1) и, наконец, при помощи расширенного алгоритма Евклида раскрывает значение d2 по формуле
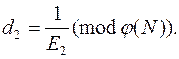
Предположим, что теперь атакующий не принадлежит к пользователям криптосистемы, использующей общий модуль. Допустим, происходит рассылка одинакового (допустим циркулярного) сообщения m двум клиентам криптосистемы, открытые ключи которых
(N, E1) и (N, E2).
Противник, нападающий извне, видит зашифрованные сообщения С1 и C2, где
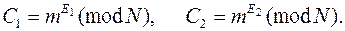
Он может вычислить

и восстановить сообщение m по следующей схеме:
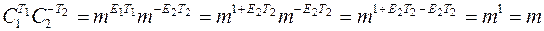
Пример.N = N1 = N2 = 18923, E1 = 11 и E2 = 5.
Предположим, что перехвачены шифртексты
C1 = 1514 и C2 = 8189,
соответствующие одному открытому тексту m. Тогда противник вычисляет T1 = 1 и T2 = 2, после чего раскрывает исходную информацию:
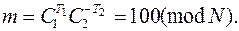
Вывод. При использовании общего модуля N любой законный пользователь системы может восстановить секретную экспоненту d другого пользователя, а внешний противник сможет читать циркулярные сообщения m.
Малые шифрующие экспоненты:
Иногда в криптосистемах RSA с целью экономии затрат на шифрование используются небольшие шифрующие экспоненты E. Это тоже создает дополнительные проблемы, связанные с криптостойкостью. Предположим, что есть три пользователя с различными модулями шифрования
N1, N2 и N3
и одинаковой шифрующей экспонентой E = 3. Пусть некто посылает им одно сообщение m, зашифрованное тремя разными открытыми ключами. Нападающий видит три криптограммы:
C1 = m3 (mod N1),
C2 = m3 (mod N2),
C3 = m3 (mod N3)
и с помощью китайской теоремы об остатках находит решение системы
{X = Ci (mod Ni)| i = 1, 2, 3}
в виде
X = m3 (mod N1N2N3).
Но поскольку m3 < N1N2N3, целые числа X и m3 должны совпадать. Поэтому, вычисляя обычный кубический корень из X, нападающий раскрывает сообщение m.
Пример.
N1 = 323, N2 = 299, N3 = 341
и перехваченные сообщения
C1 = 50, C2 = 299, C3 = 1,
Чтобы восстановить исходное сообщение m, находим решение системы
X = 300763 (mod N1N2N3),
после чего извлекаем обычный кубический корень
m = X1/3 = 67.
Вывод. При использовании малой шифрующей экспоненты E противник может восстановить циркулярное сообщение m для E пользователей.
Обе вышеуказанные атаки позволяют раскрыть текст, не прибегая к разложению на множители. Наиболее важный вывод из них – необходимость дополнять оригинальные сообщения случайными цифрами перед их зашифрованием.
При практической реализации RSA необходимо решить следующие задачи:
1. Генерация больших простых чисел p и q с проверкой выполнения соответствующих требований к ним.
2. Выбор экспонент e и d с соблюдением соответствующих требований.
3. Реализация операции вычисления xy(mod n).
Генерация большого простого числа:
1) Сгенерировать случайное n-битовое число p.
2) Установить старший и младший бит равными 1. (Старший бит гарантирует требуемую длину простого числа, а младший – обеспечивает его нечетность).
3) Убедиться, что p не делится на малые простые числа: 3, 5, 7, 11 и т.д. Во многих практических реализациях проверяется делимость p на все простые числа, меньшие 256. Наиболее надежна проверка делимости на все простые числа, меньшие 2000. Эти проверки можно выполнить на основе массива этих простых чисел.
4) Выполнить тест простоты Рабина-Миллера для некоторого случайного числа a. Если p проходит тест, сгенерировать другое случайное число a и повторить тест. Для ускорения проверки можно выбирать относительно небольшие значения a. Выполнить тест минимум пять раз. Если p не проходит один из тестов, то перейти к шагу 1).
Другой путь – не генерировать случайное число p в каждом тесте, а последовательно перебирать все нечетные числа, начиная со случайно выбранного числа, пока не найдется простое число.
Тест Рабина-Миллера:
Выбрать для тестирования число p. Вычислить b – число делений p – 1 на 2 (то есть 2b – это наибольшая степень числа 2, на которую делится p – 1). Затем вычислить m, такое, что p = 1 2b · m.
1) Выбрать случайное число a, меньшее p.
2) Установить j = 0 и z = am mod p.
3) Если z = 1 или если z = p – 1, то p проходит тест и может быть простым числом.
4) Если j > 0 и z = 1, то p не относится к простым числам.
5) Установить j = j 1. Если j < b и z ¹ (p – 1), установить z = z2 mod p и вернуться к шагу 4). Если z = p – 1, то p проходит тестирование и может быть простым числом.
6) Если j = b и z ¹ (p – 1), то p не относится к простым числам.
Выбор экспонент e и d:
1) Так как единственное требование к e – отсутствие общих множителей с числом φ(n) = (p – 1) · (q – 1), то логично выбирать небольшое e легко разложимое на простые множители и осуществлять проверку делением φ(n) на множители e. Либо выбирать простое e. Неплохо также выбирать e с минимальным количеством единиц в двоичном представлении, что ускорит операцию возведения в степень, реализованную следующим алгоритмом.
2) Так как очевидно, что d = e-1(mod p), то d находим при помощи расширенного алгоритма Евклида.
Алгоритм вычисления xy(mod n).
1) Представим y в двоичной системе счисления y = y02r … yr-12 yr, где yi, цифры в двоичном представлении равные 0 или 1, y0 = 1.
2) Положим x0 = x и затем для i = 1,…, r вычислим
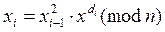 .
.
3) xr есть искомый вычет xy(mod n).
§
Односторонняя функция – возведение в степень с фиксированным модулем P и основанием G.
H = Gx (mod P)
Обратная задача – задача дискретного логарифмирования
x = ind G,P H
является сложной.
Здесь опишем шифрование по Эль-Гамалю, использующее конечные поля. Существует и аналогичная система на эллиптических кривых.
В отличие от RSA, в алоритме Эль-Гамаля существуют некоторые открытые параметры, которые могут быть использованы большим числом пользователей. Они называются параметрами домена и выглядят следующим образом:
– P – «большое простое число», то есть число, насчитывающее около 1024 бит, такое, что P – 1 делится на другое, «среднее простое число» Q, лежащее неподалеку от 2160.
– G – элемент мультипликативной группы поля 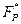 , порядок которой, как мы знаем делится на Q, причем
, порядок которой, как мы знаем делится на Q, причем
G(P – 1)/Q (mod P) ≠ 1.
Все параметры домена, то есть P, Q и G, выбираются таким образом, чтобы элемент G(P – 1)/Q был образующей абелевой группы A порядка Q. Информация об этой группе открыта и используется большим числом пользователей.
После выбора параметров домена определяют открытый и закрытый ключи. Закрытым ключом может априори быть любое натуральное число x, а открытый ключ получается по следующей формуле:
H = Gx (mod P).
Обратите внимание на то, что каждый из пользователей RSA должен генерировать два больших простых числа для определения ключевой пары, что является довольно громоздкой задачей, а в системе Эль-Гамаля для построения ключевой пары достаточно найти какое-нибудь случайное число и сделать сравнительно несложные вычисления в арифметике остатков.
Сообщение в этой ситеме представляется ненулевым элементом поля 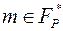 . Для его шифрования поступают следующим образом:
. Для его шифрования поступают следующим образом:
– генерируют случайный эфемерный ключ k,
– вычисляют C1 = Gk,
– находят C2 = m · Hk,
– выдают получившийся шифртекст в виде пары С = (С1, С2).
Заметим, что при каждом шифровании применяется свой кратковременный ключ k. Поэтому, шифруя одно сообщение дважды, мы получаем разные шифртексты.
Чтобы расшифровать пару данных С = (С1, С2), производят следующие преобразования:

Пример.Q = 101, P = 809 и G = 3.
Легко проверить, что Q действительно делит число P – 1, а порядок элемента G в группе 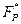 делится на Q. Порядок элемента G равен 808, поскольку
делится на Q. Порядок элемента G равен 808, поскольку
3808 = 1 (mod P),
и ни при каких меньших степенях такого равенства не получается.
В качестве пары открытого и закрытого ключа выберем
x = 68 и H = Gx = 368 = 65 (mod P).
Допустим, нам нужно зашифровать сообщение, численное представление которого равно
m = 100. Поступаем следующим образом.
– Генерируем случайный эфемерный ключ k = 89.
– Находим С1 = Gk = 389 = 345 (mod P).
– Получаем С2 = m · Hk = 100 · 6589 = 517 (mod P).
– Отправляем шифртекст C = (345, 517).
Адресат сможет восстановить текст, делая также вычисления:
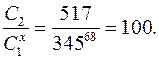
Последнее равенство получается чуть более сложно, чем в вещественных числах: сначала число 345 возводится в степень 68 по модулю 809, вычисляется мультипликативный обратный к результату по этому же модулю, а затем найденный обратный умножается на 517.
Практическая стойкость шифров.
Правила криптоанализа были сформулированы еще в конце XIX века преподавателем немецкого языка в Париже голландцем Керкхофом . Согласно одному из этих правил разработчик шифра должен оценивать криптографические свойства шифра в предположении, что не только шифртекст известен противнику (криптоаналитику противника), но известен и алгоритм шифрования, а секретным для него является лишь ключ.
Основными количественными мерами стойкости шифра служат так называемые «трудоемкость метода криптографического анализа» и «надежность его». Обозначим через А – класс применимых к шифру алгоритмов дешифрования и через Τ(ϕ) – трудоемкость реализации алгоритма ϕ на некотором вычислителЬном устройстве.
Трудоемкость дешифрования обычно измеряется усредненным по ключам шифра и открытым текстам количеством времени или условных вычислительных операций, необходимых для реализации алгоритма. За трудоемкость дешифрования принимают величину
min ET(ϕ), ϕ 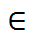 A.
A.
В предположении о вероятностных распределениях случайных действий алгоритма и неизвестных нам входных данных алгоритма, а также вероятностных характеристик выбора ключа в шифре при зашифровании случайного открытого текста подсчитывается среднее число операций (действий) алгоритма, которое и называется трудоемкостью метода криптоанализа. При фиксации в предположениях вычислительных способностей противника (производитель- ность ЭВМ, объем возможных памятей и т. д.) это среднее число операций адекватно переводится в среднее время, необходимое для дешифрования шифра.
Второй количественной мерой стойкости шифра относительно метода криптоанализа является надежность метода π(ϕ) – вероятность дешифрования.
Раз метод несет в себе определенную случайность, например, не полное опробование ключей, то и положительный результат метода возможен с некоторой вероятностью. Блестящим примером является метод дешифрования,
заключающийся в случайном отгадывании открытого текста. В ряде случаев представляет интерес и средняя доля информации, определяемая с помощью метода. В методах криптоанализа с предварительным определением ключа можно полагать, что средняя доля информации – это произведение вероятности его определения на объем дешифрованной информации. Конечно, используют и другие характеристики эффективности методов криптоанализа, например, вероятность дешифрования за время, не превосходящее Т.
Под количественной мерой криптографической стойкости шифра понимается наилучшая пара (Τ(ϕ),π(ϕ)) из всех возможных методов криптографического анализа шифра. Смысл выбора наилучшей пары состоит в том, чтобы выбрать метод с минимизацией трудоемкости и одновременно максимизацией его надежности.
Вопросы имитозащиты.
Имитостойкость шифров.
Предположим, что имеется связь между абонентами А и В. Абонент А может в определенный момент времени отправить абоненту В сообщение «у» – криптограмму, зашифрованную шифром (Χ,Κ,Υ,f) на ключе k 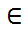 К (здесь в рассуждениях мы используем модель шифра Шеннона, где под X понимается множество открытых (содержательных) текстов). До момента передачи у
К (здесь в рассуждениях мы используем модель шифра Шеннона, где под X понимается множество открытых (содержательных) текстов). До момента передачи у 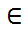 У канал связи «пуст», но в шифратор абонента В введен ключ k в ожидании получения сообщения от абонента А.
У канал связи «пуст», но в шифратор абонента В введен ключ k в ожидании получения сообщения от абонента А.
Возможные действия противника сформулируем в виде предположений
о его возможностях:
– он знает действующий шифр;
– он имеет доступ к каналу связи ;
– он может считывать из канала любое сообщение;
– он может формировать и вставлять в канал связи любое сообщение;
– он может заменять передаваемое сообщение на любое другое сообщение;
– все указанные действия он может совершать «мгновенно» (располагая соответствующими техническими средствами);
– он не знает действующего ключа шифра.
Пусть (У,К,Хʽ,Х,Ф) – шифр расшифрования, X – множество содержательных открытых текстов, X 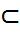 X. Уравнение расшифрования у
X. Уравнение расшифрования у 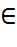 У при ключе k
У при ключе k 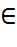 Κ будет записываться в виде: k-1 у=х, х
Κ будет записываться в виде: k-1 у=х, х 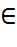 Хʽ.
Хʽ.
Пусть канал связи «пуст» и противник вставляет в канал связи некоторое шифрованное сообщение – элемент у 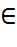 У. При действующем ключе k абонент В расшифрует у. Априори возможны два исхода:
У. При действующем ключе k абонент В расшифрует у. Априори возможны два исхода:
1) он получит k-1у 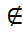 Х, то есть абонент В не прочтет сообщение и сочтет его за ложное сообщение (напомним, что в качестве X выступает множество всех содержательных текстов);
Х, то есть абонент В не прочтет сообщение и сочтет его за ложное сообщение (напомним, что в качестве X выступает множество всех содержательных текстов);
2) k-1у 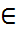 Х. В этом случае В получит открытое ложное сообщение х= k-1у и действуя в соответсвии с этим сообщением может нанести себе ущерб.
Х. В этом случае В получит открытое ложное сообщение х= k-1у и действуя в соответсвии с этим сообщением может нанести себе ущерб.
Заметим, что при таком «навязывании» ложной информации противник не знает какое именно сообщение х 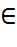 Х (во втором случае) он «навязал» абоненту В. Такое навязывание ложной информации можно назвать навязыванием «наугад». При случайно выбираемом ключе k событие: k-1у
Х (во втором случае) он «навязал» абоненту В. Такое навязывание ложной информации можно назвать навязыванием «наугад». При случайно выбираемом ключе k событие: k-1у 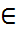 Х имеет свою вероятность
Х имеет свою вероятность
Рн(у)=Р(k-1у 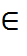 Х),
Х),
называемую вероятностью навязывания криптограммы у. Считается естественным, что противник выберет навязываемый у 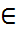 У так, чтобы максимизировать вероятность Рн(у)· Защищающаяся сторона, в свою очередь, зная о возможных действиях противника, будет выбирать такой шифр, в котором максимальное значение вероятностей навязывания Рн = mах Р(k-1у
У так, чтобы максимизировать вероятность Рн(у)· Защищающаяся сторона, в свою очередь, зная о возможных действиях противника, будет выбирать такой шифр, в котором максимальное значение вероятностей навязывания Рн = mах Р(k-1у 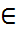 Х) минимально.
Х) минимально.
Величину 1/Рн назвают коэффициентом имитозащиты в пустом канале. При навязывании противником «наилучших» криптограмм у,: Рн(у,)= Рн величина 1/Рн характеризует среднее число попыток противника до навязывания ложной информации (предполагается случайный выбор ключей при каждой попытке).
Противник может ужесточить свои действия: пусть х(0) 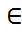 Х – сообщение, которое наносит максимальный ущерб абоненту В; противник может попытаться навязывать такое сообщение у
Х – сообщение, которое наносит максимальный ущерб абоненту В; противник может попытаться навязывать такое сообщение у 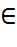 У, при котором вероятность Р(k-1у = х(0)) максимальна. Такой способ навязывания можно назвать целевым (прицельным).
У, при котором вероятность Р(k-1у = х(0)) максимальна. Такой способ навязывания можно назвать целевым (прицельным).
Аналогичные ситуации возникают и при навязывании путем подмены передаваемого сообщения. Противник может обладать и дополнительной информацией (не отраженной выше в перечне его возможностей). Например, может знать открытый текст х 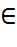 Х, который скрывается за криптограммой у в канале связи. Аналогично вводится величина max Р(k -1 у’
Х, который скрывается за криптограммой у в канале связи. Аналогично вводится величина max Р(k -1 у’ 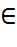 Χ) характеризующая стремление противника максимизировать условную вероятность навязывания, а защищающаяся сторона стремится минимизировать этот максимум.
Χ) характеризующая стремление противника максимизировать условную вероятность навязывания, а защищающаяся сторона стремится минимизировать этот максимум.
Общая задача защищающийся стороны состоит в выборе такого шифра, который минимизирует ущерб от имитационных действий противника во всех реально возможных ситуациях.
Шифр является наилучшим по имитозащите в пустом канале в том и только в том случае, если для любого у 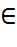 У справедливо
У справедливо
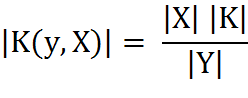
Для наилучшего шифра по имитозащите в пустом канале коэффициент эмитозащиты 1/Рн = 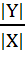 . Он совпадает со среднем числом попыток про- тивника «наугад» (случайно и равновероятно) навязывания у
. Он совпадает со среднем числом попыток про- тивника «наугад» (случайно и равновероятно) навязывания у 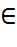 У до получения «успеха» – навязывания ложной информации (предполагается, что при каждой попытке ключ наилучшего по имитозащите в пустом канале шифра выбирается случайно и равновероятно).
У до получения «успеха» – навязывания ложной информации (предполагается, что при каждой попытке ключ наилучшего по имитозащите в пустом канале шифра выбирается случайно и равновероятно).
Шифр является наилучшим по имитозащите путем подмены в том и только в том случае, если для любых у,у`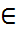 У справедливо
У справедливо
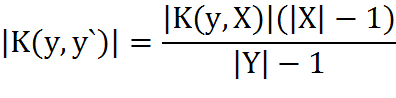
В этом случае
РH(y,y`) 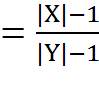
Под обеспечением имитостойкости приемного устройства понимается его защита от навязывания информации, поступающей в результате воздействия противника на передаваемую по каналу связи информацию, а также и на «пустой канал». Ложная информация считается навязанной, если она принята приемным устройством к исполнению (то есть принята также как принимается истинное сообщение). Воздействие помех в канале связи на передаваемую информацию также трактуется как попытка навязывания ложной информации. Для узнавания факта навязывания информации и предусмотрена имитозащита.
Для защиты от перехваченных и повторно переданных шифрсообщений используют метки времени (проставляя время отправления в открытом сообщении ). В случае, когда отмеченное время отличается от времени принятия сообщения на величину, превышающую некоторый допустимый предел, приемное устройство делает вывод о принятии ложного сообщения. В некоторых случаях используют секретный алгоритм изменения ключа шифра через короткие промежутки времени. Если задержка в приеме превышает величину этого промежутка, то приемник не расшифрует навязываемое сообщение.
Для защиты от ложных навязываемых сообщений используют имитовставки. При передаче сообщения а 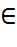 А (на передающем устройстве) вырабатывают гамму G
А (на передающем устройстве) вырабатывают гамму G 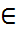 Г и по каналу связи передают пару (a,z), где z=F(a,G). На приемном устройстве с помощью шифра вырабатывается та же самая гамма G и проверяется для принятой из канала пары (a`,z`) совпадение значения F(a` G) со значением z` При совпадении значений делается вывод о приеме истинного сообщения. В противном случае, делается вывод о приеме ложного сообщения.
Г и по каналу связи передают пару (a,z), где z=F(a,G). На приемном устройстве с помощью шифра вырабатывается та же самая гамма G и проверяется для принятой из канала пары (a`,z`) совпадение значения F(a` G) со значением z` При совпадении значений делается вывод о приеме истинного сообщения. В противном случае, делается вывод о приеме ложного сообщения.
Коды аутентификации сообщений (Message authentication codes или MACs) — это следующий базисный элемент защиты сообщений. Они не обеспечивают секретность, но гарантируют аутентификацию и целостность. Они дают уверенность, что сообщение пришло именно от того источника, который обозначен как автор (это аутентификация), и что сообщение по пути не изменилось (а это целостность). Можно рассматривать MAC как защищающую от вскрытия оболочку сообщения. Кто угодно может прочесть сообщение — оболочка не обеспечивает секретность. Но кто-то, кто знает ключ MAC, может удостовериться, что сообщение не было изменено. Конкретнее, MAC — это номер, который прикреплен к цифровому сообщению.
Для MAC применяют секретные ключи совместного использования, типа симметричных алгоритмов шифрования. Сначала корреспонденты договариваются о ключе . Затем отправитель вычисляет MAC сообщения (применяя секретный ключ) и присваивает его сообщению. У каждого сообщения есть уникальный MAC для любого возможного ключа. Когда получатель получает сообщение, он вычисляет его MAC (опять-таки используя все тот же совместный ключ) и сравнивает его с присланным значением. Если они совпадают, то он может быть уверен в двух вещах : сообщение действительно пришло от условленного отправителя (или от кого-то, кто знает секрет общего ключа) — потому что только применяя этот ключ, можно вычислить MAC, и это сообщение цельное и не измененное — так как MAC можно вычислить только по полному и точному сообщению.
Помехоустойчивость шифров.
Для определения понятия помехоустойчивости шифров используем модель так называемых эндоморфных шифров (термин предложил К. Шеннон), то есть шифров (Χ,Κ,Υ,f), для которых множество открытых текстов X совпадает с множеством криптограмм У. Для таких шифров (Χ,Κ,Υ,f) каждое преобразование fk, k 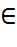 K является биекцией X в X (подстановкой на X). Множество таких биекций обозначают через П(K,f)={fk: k
K является биекцией X в X (подстановкой на X). Множество таких биекций обозначают через П(K,f)={fk: k 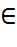 Κ}, а сам эндоморфный шифр – через Α=(Χ,Π(Κ,f)) и называют подстановочной моделью эндоморфного шифра. При этом под ключом этого шифра понимают биекцию π
Κ}, а сам эндоморфный шифр – через Α=(Χ,Π(Κ,f)) и называют подстановочной моделью эндоморфного шифра. При этом под ключом этого шифра понимают биекцию π 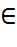 Π(Κ,f). Уравнение шифрования записывают в виде
Π(Κ,f). Уравнение шифрования записывают в виде 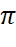 х=у, уравнение расшифования записывают в виде π-1y=x.
х=у, уравнение расшифования записывают в виде π-1y=x.
В дальнейшем, для определенности, будем считать, что множество X – это множество текстов одной и той же длины L в некотором алфавите Ω, X = QL.
Под искажением сообщения при его передаче по каналу связи понимается замена шифрованного сообщения у 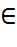 У на некоторое другое у*, у*
У на некоторое другое у*, у* 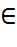 У*. Характер (правило) замены определяется физическим состоянием как самого канала связи, так и окружающей его cреды, У≤У*.
У*. Характер (правило) замены определяется физическим состоянием как самого канала связи, так и окружающей его cреды, У≤У*.
Примером искажений являются так называемые искажения типа замены. Передаваемое по каналу связи сообщение у=Ь1Ь2,…bl заменяется на сообщение y`=b`1,b`2…b`L. Имеется в виду, что исказиться может любая буква bj сообщения у, при этом искажении она заменится на букву b`j. Примерами других искажений являются искажения типа «пропуск», «вставка». Искажение типа пропуска букв состоит в том, что из сообщения у=Ь1Ь2,…bl пропадут одна или несколько букв, стоящих на некоторых местах. Искажение типа вставки состоит в добавлении одной или нескольких букв алфавита Ω в сообщение y=b1,b3,…,bL.







