Поиск рефератов, курсовых, дипломных, контрольных работ
Результаты по запросу
«различные средние для нескольких отрезков»
– 115, стр. 11 из 12
Международное частное право в средние века
(Рефераты, Государство и право)
Абсолютные и относительные величины. Средние величины и показатели вариации
(Учебные пособия, Экономика)
Политико-правовая идеология в странах Арабского Востока в средние века
(Рефераты, Остальные рефераты)
Арабо-исламская философия в средние века
(Рефераты, Философия)
Рыцарская культура в системе культуры средневековья. Образование и образованность в средние века
(Рефераты, Культура и искусство)
Семь чудес света – древний мир, средние века и наше время (история цивилизации, реферат)
(Рефераты, История)
Способы получения сложных эфиров. Конденсации формальдегида с изобутиленом. Различные способы получения фенола
(Рефераты, Химия)
Различные подходы к определению количества информации. Единицы измерения количества информации
(Учебные пособия, Педагогика)
Анализ техники бега на различные дистанции, анализ техники прыжков в высоту с разбега способами “перешагивание” и “фосбери-флоп”
(Рефераты, Физкультура и спорт)
Право. Средние века
(Доклады, Право)
Среднее пропорциональное / построения циркулем и линейкой / треугольники / справочник по геометрии 7-9 класс
Среднее пропорциональное положительных чисел 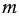 и
и 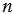 – это такое число
– это такое число 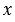 , которое равно квадратному корню из произведения этих чисел, т.е.
, которое равно квадратному корню из произведения этих чисел, т.е. 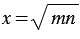 .
.
Среднее пропорциональное носит такое название, потому что число 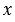 является средним членом пропорции
является средним членом пропорции 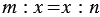 .
.
Средним пропорциональным (или средним геометрическим) двух отрезков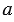 и
и 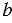 , называется такой отрезок
, называется такой отрезок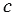 , что:
, что: 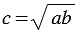 .
.
Чтобы построить среднее пропорциональное двух отрезков используют циркуль и линейку.
Ход построения:
Пусть нам даны два отрезка 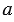 и
и 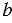 , строим их.
, строим их.
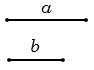
Затем строим с помощью линейки прямую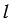 , отмечаем на ней точкуА и строим отрезокАЕ, равный отрезку
, отмечаем на ней точкуА и строим отрезокАЕ, равный отрезку 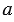 . Для этого строим с помощью циркуля окружность радиуса
. Для этого строим с помощью циркуля окружность радиуса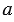 с центромА (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезокЕВ, равный отрезку
с центромА (полностью окружность строить необязательно, смотри выделенное красным цветом). Затем, аналогично строим отрезокЕВ, равный отрезку 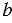 .
.
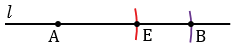
Далее найдем середину отрезкаАВ. Для этого строим две окружности с центрами А и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая пересечет отрезок АВ в его середине О.
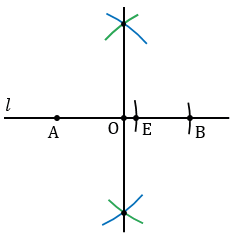
Теперь строим окружность с центромО радиуса ОА.
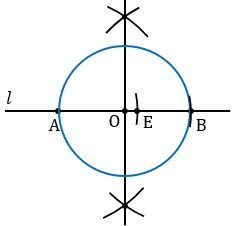
Затем построим перпендикуляр к прямой 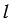 так, чтобы он проходил через точкуЕ, которая делит отрезок АВ в отношении
так, чтобы он проходил через точкуЕ, которая делит отрезок АВ в отношении 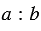 . Для этого строим окружность произвольного радиуса с центромЕ (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую
. Для этого строим окружность произвольного радиуса с центромЕ (полностью окружность строить необязательно, смотри выделенное фиолетовым цветом), данная окружность пересечет прямую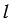 в двух точках М и В (точкуВ мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центромЕ и прямой
в двух точках М и В (точкуВ мы берем как точку пересечения данной окружности и данной прямой для того, чтобы не добавлять на рисунке лишние элементы, но важно помнить, что точки пересечения окружности с центромЕ и прямой 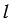 могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центромЕ). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой
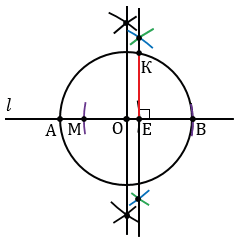
могут быть и другие, все зависит от того, каким мы возьмем радиус окружности с центромЕ). Далее строим две окружности с центрами М и В так, чтобы они пересекались в двух точках (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Через точки пересечения данных окружностей проводим прямую, которая будет перпендикулярна к прямой 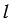 и пересечет окружность с центромО в точке К.
и пересечет окружность с центромО в точке К.
Длина отрезкаЕК и есть искомый отрезок 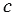 , равный среднему пропорциональному отрезков
, равный среднему пропорциональному отрезков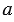 и
и 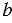 , т.е.
, т.е. 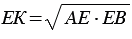 или
или 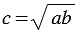 .
.






