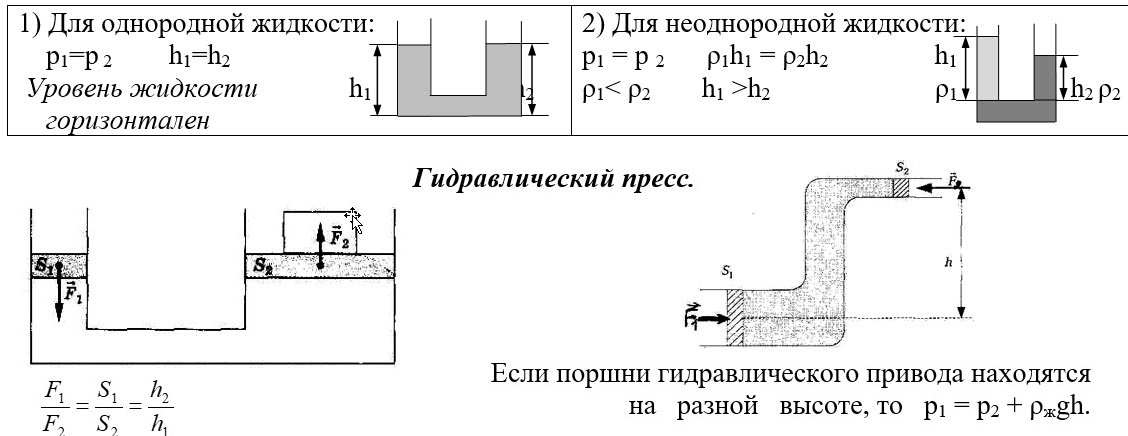
- Задачи на давление жидкостей и газов с ответами и решениями
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
- Краткая теория по теме «Задачи на давление жидкостей»
- Задачи на Сообщающиеся сосуды
- Ρ1gh1 + ρ2gh2 = ρ3gh3 + ρ4gh4
- СТАТИКА И ГИДРОСТАТИКА Теория и формулы (кратко)
- Виды равновесия.
- Простые механизмы и блоки
- Гидростатика.
- ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ГИДРОСТАТИКЕ
- БУЛЫНИН, ЦО № 17 ЦАО, г. Москва
- Ход урока
- Задача #3321
- Задача #3322
- Задача #3323
- Задача #3324
- Задача #3331
- Задача #3341
- Задача #3342
- Задача #3343
- Задача #3344
- Задача #3381
- Задача #338NaN
- Задача #3392
- Задача #3393
- Задача #3394
Задачи на давление жидкостей и газов
с ответами и решениями
Формулы, используемые на уроках «Задачи на давление жидкостей и газов».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Определить давление бензина на дно цистерны, если высота столба бензина 2,4 м, а его плотность 710 кг/м3.
ОТВЕТ: 17,04 кПа.

Задача № 2.
Какая жидкость находится в сосуде, если столб высотой 0,3 м оказывает давление 5400 Па ?
ОТВЕТ: Серная кислота (1800 кг/м3).

Задача № 3.
Плотность спирта 800 кг/м3. Какова будет высота столба спирта при давлении 2,4 кПа?
ОТВЕТ: 0,3 м. Чтобы увидеть решение, нажмите на спойлер ниже.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 4.
В цилиндре с маслом на поршень действует сила 40 Н. Чему равна сила давления на внутреннюю поверхность цилиндра площадью 8 дм2? Площадь поршня 2,5 см2. Вес масла не учитывайте.
ОТВЕТ: 12,8 кН.

Задача № 5.
Вычислите давление и силу давления керосина на дно бака площадью 50 дм2, если высота столба керосина в баке 40 см.
ОТВЕТ: 3200 Па; 1600 Н.

Задача № 6.
В мензурку, площадь дна которой 20 см2, налита вода до высоты 10 см. Сколько граммов воды налито? Чему равно давление воды на дно мензурки?

Задача № 7.
Рыба камбала находится на глубине 1200 м и имеет площадь поверхности 560 см2. С какой силой она сдавливается водой?
ОТВЕТ: 678 кН.

Задача № 8.
На какой глубине давление воды в море равно 412 кПа?
ОТВЕТ: 40 м.

Задача № 9.
Поршневой насос может произвести давление 5 • 105 Па. На какую высоту можно поднять воду этим насосом?
ОТВЕТ: 51 м.

Задача № 10.
В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают расплавленный металл. Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке слева изображена изложница, справа — подъем изложницы с отлитого слитка. Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7000 кг/м3.
ОТВЕТ: 17 кН.

Задача № 11.
Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?
ОТВЕТ: ртути — 75 см, спирта — 12,76 см.

Задача № 12.
Батискаф опустился в море на глубину 50 м. Каково давление на поверхность батискафа на данной глубине? (Плотность морской воды 1010 кг/м3.)
ОТВЕТ: 606 кПа.

Задача № 13.
Человек стоит на кожаном мешке с водой. Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающейся с мешком поверхности платформы 1000 см2.
ОТВЕТ: 0,75 м.

Задача № 14 (повышенной сложности).
Брусок массой m = 2 кг имеет форму параллелепипеда. Лежа на одной из граней, он оказывает давление p1 = 1 кПа, лежа на другой — давление 2 кПа, стоя на третьей — давление 4 кПа. Каковы размеры бруска?
ОТВЕТ: 5 см, 10 см, 20 см.
Задача № 15 (олимпиадный уровень).
Оцените массу атмосферы Земли (радиус Земли R = 6400 км)
ОТВЕТ: примерно 5 • 1018 кг.
Указание к РЕШЕНИЮ. Вес атмосферы равен силе давления воздуха на всю поверхность Земли, площадь которой S = 4πR2. Следовательно, mg = ра • 4πR2, где ра = 105 Па — атмосферное давление. Отсюда m = 4πR2 ра /g = 5 • 1018 кг. Эта величина составляет менее одной миллионной части полной массы нашей планеты. Такая простая оценка массы атмосферы возможна потому, что основная часть атмосферы сосредоточена на высотах, малых по сравнению с радиусом Земли. Поэтому можно считать, что вес атмосферы равен mg, где g — ускорение свободного падения вблизи поверхности Земли.
Краткая теория по теме «Задачи на давление жидкостей»
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Вы смотрели конспект урока «Задачи на Давление жидкостей с ответами и решениями». Выберите дальнейшие действия:
Задачи на Сообщающиеся сосуды
Теоретический материал, используемый для решения задачи на сообщающиеся сосуды смотрите в конспекте «Сообщающиеся сосуды. Гидравлический пресс. Шлюзы».
Сообщающиеся сосуды — два или более соединённых между собой сосудов (ниже уровни жидкости), в которых жидкость может свободно перетекать из одного сосуда в другой.
Закон сообщающихся сосудов: в открытых сообщающихся сосудах любой формы при равновесии давление жидкости на любом горизонтальном уровне одинаково.
Схематически это выглядит таким образом, что в точках А и В ⇒.

Ρ1gh1 + ρ2gh2 = ρ3gh3 + ρ4gh4
Обратите внимание! Ниже уровня, на котором находятся точки А и В, жидкость однородна. : р — давление, ρ — плотность, h — высота, g — ускорение свободного падения (9,8 м/с^2).
: в открытых сообщающихся сосудах при равновесии высоты столбов жидкостей, отсчитываемые от уровня, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.

: в открытых сообщающихся сосудах при равновесии однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.
В гидравлическом прессе сообщающиеся сосуды разных сечений S2 и S1 заполненные однородной жидкостью, используют для получения выигрыша в силе — F2/F1, равного — S2/S1.

Задача № 1.
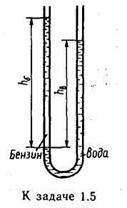
В левом колене сообщающихся сосудов налита вода, в правом — керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
Ответ: 0,04 м (или 4 см).

Задача № 2.
В сообщающихся сосудах находятся ртуть и вода. Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?
Ответ: 0,85 м (или 85 см). Чтобы увидеть решение задачи, нажмите на спойлер ниже.
Задача № 3.
Уровень жидкостей в сосудах одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
Задача № 4.
В сообщающихся сосудах находятся ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?
Ответ: 0,335 м (или 33,5 см).

Задача № 5.
Площадь малого поршня гидравлического пресса равна 10 см2, большого — 50 см2. На малый поршень поместили гирю массой 1 кг. Какой груз нужно поместить на большой поршень, чтобы жидкость осталась в равновесии?
Ответ: 5 кг.

Задача № 6.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Ответ: 2,7 м.

Задача № 7.
В U-образный сосуд налито 3 жидкости: вода, мед и масло. Высота воды в левом колене 40 см, высота масла в правом колене 30 см. Найдите разницу высот столбов меда в левом и правом коленах. Ответ округлить до сотых.
Ответ: ≈ 0,09 м.
Задача № 8.
В цилиндрических сообщающихся сосудах находится ртуть. Площадь поперечного сечения широкого сосуда в пять раз больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают воду, которая образует столб высотой 34 см. На сколько поднимется уровень ртути в широком сосуде и на сколько опустится в узком?
Ответ: в широком сосуде на 0,42 см, в узком — на 2,1 см.
Задача № 9.
Высота воды в левом колене сообщающихся сосудов h1 = 40 см, в правом h2 = 10 см. В каком направлении будет переливаться вода, если открыть кран? На сколько изменится уровень воды в левом сосуде? Найти объем воды, который перелился из одного сосуда в другой. Левое колено сосуда имеет площадь поперечного сечения S1 = 10 см2, правое S = 20 см2.
Ответ: в правый; 0,2 м; 0,2 л.

Задача № 10.
В два колена сообщающихся сосудов налили ртуть. После установления равновесия высота ртути оказалась равна 25 см. Затем в левый сосуд (левое колено) добавили воду. Высота столба воды оказалась равна 20 см. Определите уровень ртути в левом и правом колене после добавления воды. Плотность воды 1 г/см3. Плотность ртути 13600 кг/м3.
ОТВЕТ: в левом — 0,24265 м (≈24,3 см), в правом — 0,25735 м (≈25,7 см).
Вы смотрели: Конспект урока по физике «Задачи на Сообщающиеся сосуды и Гидравлический пресс». Выберите дальнейшие действия:
СТАТИКА И ГИДРОСТАТИКА
Теория и формулы (кратко)
Условия равновесия тела:
а) Поступательно движущееся тело находится в состоянии равновесия (покоится или движется прямолинейно и равномерно), если


Виды равновесия.
а) если ось проходит через центр масс, то тело находится в безразличном равновесии при любом положении тела (а);
б) ось выше точки центра тяжести — устойчивое равновесие (б);
в) ось ниже точки центра тяжести — неустойчивое равновесие( в).
а) если равнодействующая всех сил направлена к положению равновесия, то тело находится в устойчивом положении (рис. а);
б) если равнодействующая всех сил направлена от положения равновесия, то тело находится в неустойчивом равновесии (рис. б);
в) если Σ = 0, — равновесие безразличное (рис. в).
Если вертикаль, проведенная через центр тяжести тела, пересекает площадь его опоры, то равновесие тела устойчивое. Если не пересекает, то тело падает, — равновесие неустойчивое.
Простые механизмы и блоки
Простые механизмы — приспособления, которые служат для преобразования силы. К ним относятся: рычаг (блок, ворот) и наклонная плоскость (клин, винт). Они применяются для получения выигрыша в силе.
F2/F1 – выигрыш в силе. F1l1=F2l2 — условие равновесия рычага для двух сил.
Золотое правило механики: все простые механизмы, не дают выигрыша в работе — во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.

Гидростатика.
Давление — скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади её поверхности.
Гидростатическое давление — давление, обусловленное весом столба жидкости. Манометр — прибор для измерения давления в жидкости или газа.
p = ρжgh — давление на произвольной глубине несжимаемой жидкости
F = pS = ρжghSдна — сила давления на дно сосуда

На одном и том же уровне давление одинаково во всех направлениях.
Давление р на произвольной глубине h сжимаемой поршнем жидкости определяется давлением поршня и давлением столба жидкости р = рпорш. + ρжgh

Атмосферное давление – давление, которое производит воздушная оболочка Земли.
Опыт Торричелли (1634 г.) свидетельствует: атмосферное давление равно давлению столба ртути в трубке.
Нормальное атмосферное давление: 1 атм = 760 мм.рт.ст. = 1 01325 Па ≈ 105 Па (при 0ºС); 1 мм.рт.ст.=133,3 Па
Оно может изменяться от места к месту и во времени (циклоны и антициклоны) и убывает с увеличением высоты над уровнем моря (на каждые 12 м подъёма оно уменьшается на 1 мм. рт. ст.).
Барометры — приборы для измерения атмосферного давления. Существуют 1) жидкостный; 2) барометр — анероид (металлический).
Закон Паскаля (1653 г.) — жидкости и газы передают производимое на них давление во все стороны одинаково.
Сообщающимися называются сосуды, соединённые между собой каналом с жидкостью.
Закон Архимеда: на тело, погруженное в покоящуюся жидкость (или газ), действует выталкивающая сила, направленная вертикально верх и равная весу жидкости, вытесненной телом.
FA =ρжgVпчт FA = Рж,выт.= mж,выт g,
FA = Рвоз — Ржид. Vпчт – объём погруженной части тела. ρж — плотность жидкости или газа.
Условие плавания тел:
б) FA < mg, ρт < ρж — тело тонет;
в) FA = mg, ρт = ρж — тело находится в равновесии на любой глубине.
Условие плавания тела на поверхности FA = mg
Если тело будет плавать частично погрузившись в жидкость, то ρж/ρт=Vт/Vпчт
На этом основано применение ареометра- прибора для определения плотности жидкости.

Конспект урока «Статика и гидростатика. Теория и формулы для ЕГЭ» + шпаргалка.
Еще конспекты для 10-11 классов:
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ГИДРОСТАТИКЕ
К выполнению расчетно – графической работы
По дисциплине «Гидравлика»
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Гидравлика, или техническая механика жидкостей— это наука о законах равновесия и движения жидкостей, о способах применения этих законов к решению практических задач;
Жидкостью называют вещество, находящееся в таком агрегатном состоянии, которое сочетает в себе черты твердого состояния (весьма малая сжимаемость) и газообразного (текучесть). Законы равновесия и движения капельных жидкостей в известных пределах можно применять и к газам.
На жидкость могут действовать силы, распределенные по ее массе (объему), называемые массовыми, и по поверхности, называемые поверхностными. К первым относятся силы тяжести и инерции, ко вторым — силы давления и трения.
Давлением называется отношение силы, нормальной к поверхности, к площади. При равномерном распределении
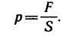
Касательным напряжением называется отношение силы трения, касательной к поверхности, к площади:
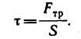
Если давление р отсчитывают от абсолютного нуля, то его называют абсолютным (рабс), а если от условного нуля (т. е. сравнивают с атмосферным давлением ра, то избыточным (ризб):
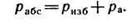
Если Рабс< Ра, то имеется вакуум, величина которого:
Рвак = Ра – Рабс
Основной физической характеристикой жидкости является плотность ρ (кг/м3), определяемая для однородной жидкости отношением ее массы m к объему V:
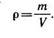
Плотность пресной воды при температуре Т = 4°С ρ = = 1000 кг/м3. В гидравлике часто пользуются также понятием удельного веса γ (Н/м3), т.е весом G единицы объема жидкости:

Плотность и удельный вес связаны между собой соотношением:
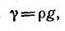
где g — ускорение свободного падения.
Для пресной воды γвод= 9810 Н/м3
Важнейшие физические параметры жидкостей, которые используются в гидравлических расчетах,— сжимаемость, температурное расширение, вязкость и испаряемость.
Сжимаемость жидкостей характеризуется модулем объемной упругости К, входящим в обобщенный закон Гука:
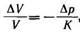
где ΔV— приращение (в данном случае уменьшение) объема жидкости V, обусловленное увеличением давления на Δр. Например, для воды Квод ≈2.103 МПа.
Температурное расширение определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С:
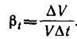
Вязкость — это способность жидкости сопротивляться сдвигу. Различают динамическую (μ) и кинематическую (ν) вязкости. Первая входит в закон жидкостного трения Ньютона, выражающий касательное напряжение τ через поперечный градиент скорости dv/dt:
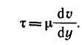
Кинематическая вязкость связана с динамической соотношением
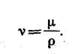
Единицей кинематической вязкости является м2/с.
Испаряемость жидкостей характеризуется давлением насыщенных паров в функции температуры.
Давлением насыщенных паров можно считать то абсолютное давление, при котором жидкость закипает при данной температуре. Следовательно, минимальное абсолютное давление, при котором вещество находится в жидком состоянии, равно давлению насыщенных паров рн.п.
Давление в неподвижной жидкости называется гидростатическим и обладает следующими двумя свойствами:
– на внешней поверхности жидкости оно всегда направлено во нормали внутрь объема жидкости;
– в любой точке внутри жидкости оно по всем направлениям одинаково, т. е. не зависит от угла наклона площадки, по которой действует.
Уравнение, выражающее гидростатическое давление р в любой точке неподвижной жидкости в том случае, когда из числа массовых сил на нее действует лишь одна сила тяжести, называется основным уравнением гидростатики:
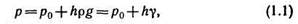
где p0 — давление на какой-либо поверхности уровня жидкости, например на свободной поверхности; h — глубина расположения рассматриваемой точки, отсчитанная от поверхности с давлением р0.
В тех случаях, когда рассматриваемая точка расположена выше поверхности с давлением р0, второй член в формуле (1.1) отрицателен.
Другая форма записи того же уравнения (1.1) имеет вид
где z и z0 — вертикальные координаты произвольной точки и свободной поверхности, отсчитываемые от горизонтальной плоскости вверх; p/(pg) — пьезометрическая высота.
Гидростатическое давление может быть условно выражено высотой столба жидкости p/ρg.
В гидротехнической практике внешнее давление часто равноатмосферному: P0=Рат
Величина давления Pат = 1 кГ/см2 = 9,81.104 н/мг называетсятехнической атмосферой.
Давление, равное одной технической атмосфере, эквивалентно давлению столба воды высотой 10 метров, т. е.

Гидростатическое давление, определяемое по уравнению (1.1), именуется полным или абсолютным давлением. В дальнейшем будем обозначать это давление рабс или p’. Обычно в гидротехнических расчетах интересуются не полным давлением, а разницей между полным давлением в атмосферным, т. е. так называемым манометрическим давлением
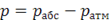
В дальнейшем изложении сохраним обозначение р за манометрическим давлением.
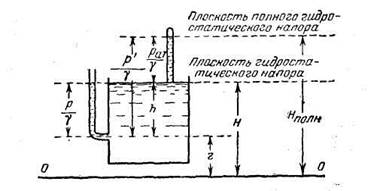
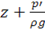
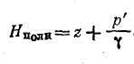
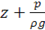
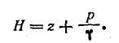
На рис. 1.1 плоскость полного гидростатического напора и плоскость гидростатического напора показаны для случая, когда свободная поверхность находится под атмосферным давлением р0=pат.
Графическое изображение величины и направления гидростатического давления, действующего на любую точку поверхности, носит название эпюры гидростатического давления. Для построения эпюры нужно отложить величину гидростатического давления для рассматриваемой точки нормально к поверхности, яа которую оно действует. Так, например, эпюра манометрического давления на плоский наклонный щит АВ (рис. 1.2,а) будет представлять треугольник ABC, а эпюра полного гидростатического давления — трапецию A’B’C’D’ (рис. 1.2,б).
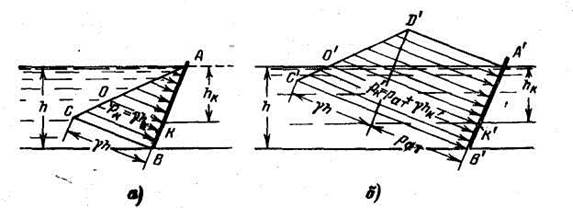
Каждый отрезок эпюры на рис. 1.2,а (например О К) будет изображать манометрическое давление в точке К, т. е. pK = ρghK, а на рис. 1.2,б — полное гидростатическое давление
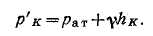
Сила давления жидкости на плоскую стенку равна произведению гидростатического давления ρс в центре тяжести площади стенки на площадь стенки S, т. е.
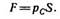
Центр давления (точка приложения силы F) расположен ниже центра тяжести площади или совпадает с последним в случае горизонтальной стенки.
Расстояние между центром тяжести площади и центром давления в направлении нормали к линии пересечения плоскости стенки со свободной поверхностью жидкости равно

где J0 — момент инерции площади стенки относительно оси, проходящей через центр тяжести площади и параллельной линии пересечения плоскости стенки со свободной поверхностью: ус — координата центра тяжести площади.
Сила давления жидкости на криволинейную стенку, симметричную относительно вертикальной плоскости, складывается из горизонтальной FГ и вертикальной FB составляющих:

Горизонтальная составляющая FГ равна силе давления жидкости на вертикальную проекцию данной стенки:

Вертикальная составляющая FB равна весу жидкости в объеме V, заключенном между данной стенкой, свободной поверхностью жидкости и вертикальной проекцирующей поверхностью, проведенной по контуру стенки.
Если избыточное давление р0 на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту) p0/(ρg)
Плавание тел и их остойчивость.Условие плавания тела выражается равенством
где G — вес тела;
Р — результирующая сила давления жидкости на погруженное в нее тело — архимедова сила.
Сила Р может быть найдена по формуле
где ρg — удельный вес жидкости;
W — объем жидкости, вытесненной телом, или водоизмещение.
Сила Р направлена вверх и проходит через центр тяжести водоизмещения.
Осадкой тела у называется глубина погружения наинизшей точки смоченной поверхности (рис. 1.3,а). Под осью плавания понимают линию, проходящую через центр тяжести С и центр водоизмещения D, соответствующий/ нормальному положению тела в состоянии равновесия (рис. 1.3, а)-
Ватерлинией называется линия пересечения поверхности плавающего тела со свободной поверхностью жидкости (рис. 1.3,б). Плоскостью плавания ABEF называется плоскость, полученная от пересечения тела свободной поверхностью жидкости, или, иначе плоскость, ограниченная ватерлинией.
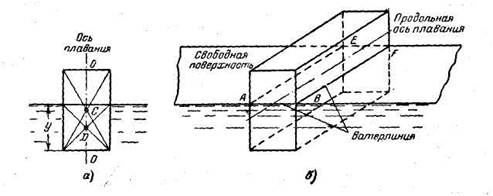
Кроме выполнения условий плавания (1.5) тело (судно, баржа и т.д.) должно удовлетворять условиям остойчивости. Плавающее тело будет остойчивым в том случае, если при крене сила веса G и архимедова сила Р создают момент, стремящийся уничтожить крен и вернуть тело в исходное положение.

При надводном плавании тела (рис. 1.4) центр водоизмещения при малых углах крена (α<15°) перемещается по некоторой дуге, проведенной из точки пересечения линии действия силы Р с осью плавания. Эта точка называется метацентром (на рис. 1.4 точка М). Будем в дальнейшем рассматривать условия остойчивости лишь при надводном плавании тела при малых углах крена.
Если центр тяжести тела С лежит ниже центра водоизмещения, то плавание будет безусловно остойчивым (рис. 1.4,а).
Если центр тяжести тела С лежит выше центра водоизмещения D, то плавание будет остойчивым только при выполнении следующего условия (рис. 1-9,б):
где ρ — метацентрический радиус, т. е. расстояние между центром водоизмещения и метацентром
δ — расстояние между центром тяжести тела С и центром водоизмещения D. Метацентрический радиус ρ находится по формуле:
где J0 — момент инерции плоскости плавания или площади, ограниченной ватерлинией, относительно продольной оси (рис. 1-8,6);
W — водоизмещение.
Если центр тяжести тела С расположен выше центра водоизмещения и метацентра, то тело неостойчиво; возникающая пара сил G и Р стремится увеличить крен (рис. 1.4,в).
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
При решении задач по гидростатике прежде всего нужно хорошо усвоить и не смешивать такие понятия, как давление р и сила F.
При решении задач на определение давления в той или иной точке неподвижной жидкости следует пользоваться основным уравнением гидростатики (1.1). Применяя это уравнение, нужно иметь в виду, что второй член в правой части этого уравнения может быть как положительным, так и отрицательным. Очевидно, что при увеличении глубины давление возрастает, а при подъеме — уменьшается.
Необходимо твердо различать давления абсолютное, избыточное и вакуум и обязательно знать связь между давлением, удельным весом и высотой, соответствующей этому давлению (пьезометрической высотой).
При решении задач, в которых даны поршни или системы поршней, следует писать уравнение равновесия, т. е. равенство нулю суммы всех сил, действующих на поршень (систему поршней).
Решение задач следует проводить в международной системе единиц измерения СИ.
Решение задачи должно сопровождаться необходимыми пояснениями, рисунками (принеобходимости), перечислением исходных величин (графа «дано»), переводом единиц в систему СИ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ГИДРОСТАТИКЕ
Задача 1. Определить полное гидростатическое давление на дно сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде h = 0,60 м.
В данном случае имеем р0=рат и потому применим формулу (1.1) в виде
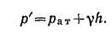
р’=9,81.104 +9810.0,6 = 103986 Па
Ответ р’=103986 Па
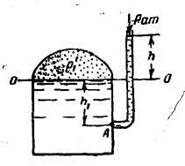
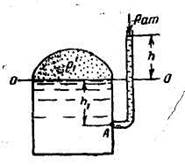
Задача 2. Определить высоту столба воды в пьезометре над уровнем жидкости в закрытом сосуде. Вода в сосуде находитcя под абсолютным давлением p’1 = 1,06ат (рисунок к задаче 2).
Составим условия равновесия для общей точки А (см. рисунок).Давление в точке А слева:
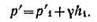
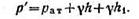
Приравнивая правые части уравнений, и сокращая на γg получаем:
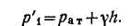
Указанное уравнение можно также получить, составив условие равновесия для точек, расположенных в любой горизонтальной плоскости, например в плоскости ОО (см. рисунок). Примем за начало шкалы отсчета пьезометра плоскость ОО и из полученного уравнения найдем высоту столба воды в пьезометре h.
Высота h равна:

= 0,6 метра
Пьезометр измеряет величину манометрического давления, выраженного высотой столба жидкости.
Ответ: h = 0,6 метра
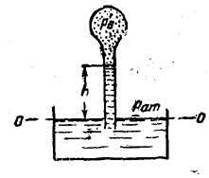
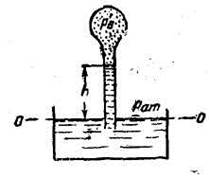
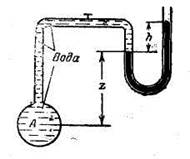
Задача 3.Определить высоту, на которую поднимается вода в вакуумметре, если абсолютное давление воздуха внутри баллона р’в=0,95 ат (рис. 1-11). Сформулировать, какое давление измеряет вакуумметр.
Составим условие равновесия относительно горизонтальной плоскости О-О:
гидростатическое давление, действующее изнутри:
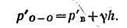
Гидростатическое давление в плоскости О—О, действующее с внешней стороны,
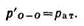
Так как система находится в равновесии, то
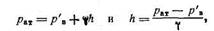
т. е. вакуумметр измеряет недостаток давления до атмосферного или вакуум, выраженный высотой столба жидкости.
Высота, на которую поднимается жидкость, при γ=9810 Н/м3

Ответ: h = 0,5 метра
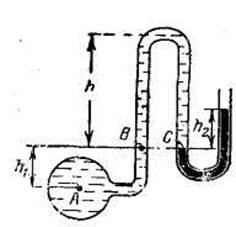
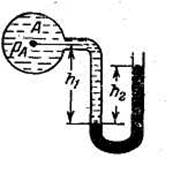
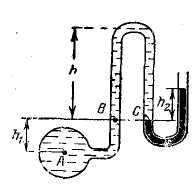
Задача 4. Определить манометрическое давление в точке А трубопровода, если высота столба ртути по пьезометру h2=25 см. Центр трубопровода расположен на h1 =40 см ниже линии раздела между водой и ртутью (рисунок к задаче).
Решение: Находим давление в точке В: р’В=р’А-γh1, так как точка В расположена выше точки А на величину h1. В точке С давление будет такое же, как в точке В, так как давление столба воды h взаимно уравновешивается, т. е.
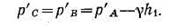
Определим давление в точке С справа с учетом атмосферного давления, т. е.
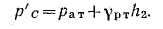
Приравнивая оба уравнения, получаем:
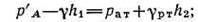
отсюда манометрическое давление:
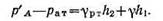
Подставляя числовые значения, получаем:
Ответ: р’А-ратм=37278 Па
Задача 1.1. Канистра, заполненная бензином и не содержащая воздуха, нагрелась на солнце до температуры 50 °С. На сколько повысилось бы давление бензина внутри канистры, если бы она была абсолютно жесткой? Начальная температура бензина 20 0С. Модуль объемной упругости бензина принять равным K=1300 МПа, коэффициент температурного расширения β = 8.10-4 1/град.
Задача 1.2. Определить избыточное давление на дне океана, глубина которого h=10 км, приняв плотность морской воды ρ=1030 кг/м3 и считая ее несжимаемой. Определить плотность воды на той же глубине с учетом сжимаемости и приняв модуль объемной упругости K = 2.103 МПа.
Задача 1.3. Найти закон изменения давления р атмосферного воздуха по высоте z, считая зависимость его плотности от давления изотермической. В действительности до высоты z=11 км температура воздуха падает по линейному закону, т. е. T=T0-βz, где β = 6,5 град/км. Определить зависимость p = f(z) с учетом действительного изменения температуры воздуха с высотой.
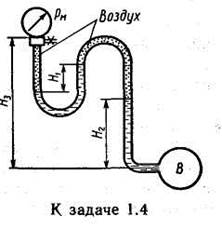
Задача 1.4. Определить избыточное давление воды в трубе В, если показание манометра рм = 0,025 МПа. Соединительная трубка заполнена водой и воздухом, как показано на схеме, причем Н1 = 0,5 м; Н2=3 м.
Как изменится показание манометра, если при том же давлении в трубе всю соединительную трубку заполнить водой (воздух выпустить через кран К)? Высота Н3 = 5 м.
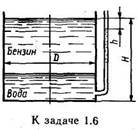
Задача 1.6.В цилиндрический бак диаметром D = 2 м до уровня Н=1,5 м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h = 300 мм. Определить веснаходящегося в баке бензина, если ρб = 700 кг/м3.
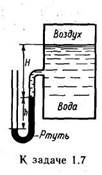
Задача 1.7. Определить абсолютное давление воздуха всосуде, если показание ртутного прибора h = 368 мм, высота H=1 м. Плотность ртути ρ= 13600 кг/м3. Атмосферное давление 736 мм рт. ст.
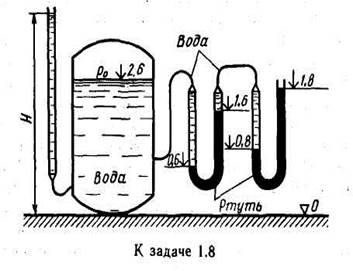
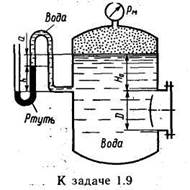
Задача 1.9.Определить силу давления жидкости (воды) на крышку люка диаметром D=l м в следующих двух случаях:
1) показание манометра рм = 0,08 МПа; H0=1,5 м;
2) показание ртутного вакуумметра h = 73,5 мм при а= 1м; ρрт= 13600 кг/м3; Н0=1,5 м.
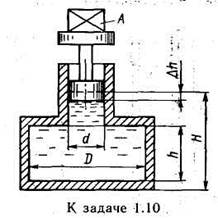
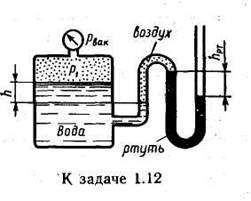
Задача 1.12. Определить абсолютное давление воздуха в баке р1, еcли при атмосферном давлении, соответствующем hа = 760 мм рт. ст., показание ртутного вакуумметра hрт = = 0,2 м, высота h =1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути ρ=13600 кг/м3.
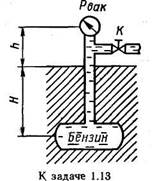
Задача 1.13. При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине Н=5 м, если показание вакуумметра, установленного на высоте h=1,7 м, равно рвак = 0,02 МПа. Атмосферное давление соответствует ра = 740 мм рт. ст. Плотность бензина ρб = 700 кг/м3.
Задача 1.15.Определить вакуум рвак и абсолютное давление внутри баллона р’в (рис. 1-11), если показание вакуумметра h =0,7 м вод. ст.
Задача 1.16. Подсчитать манометрическое и абсолютное давление в баллоне А (рисунок) в двух случаях:
1) в баллоне и в левой трубке — вода, а в правой трубке — ртуть (ρ=13600 кг/м3);
2) в баллоне и левой трубке — воздух , а в правой трубке – вода.
Определить, какой процент составляет давление столба воздуха в трубке от вычисленного во втором случае манометрического давления?
При решении задачи принять h1 = 70 см,h 2= = 50 см.
Задача 1.17. Чему будет равна высота ртутного столба h2 (рис. к задаче 1.16), если манометрическое давление нефти в баллоне А pа = 0,5 ат, а высота столба нефти (ρ=800 кг/м3) h1=55 см?
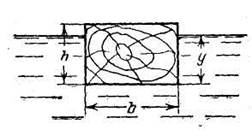
Задача 1.20. Определить удельный вес бруса, имеющего следующие размеры: ширину b=30 см, высоту h=20 см и длину l = 100 см, если его осадка y=16 см
Задача 1.21.Кусок гранита весит в воздухе 14,72 Н и 10,01 Н в жидкости, имеющей относительный удельный вес 0,8. Определить объем куска гранита, его плотность и удельный вес.
Задача 1.22 Деревянный брус размером 5,0х0,30 м и высотой 0,30м спущен в воду. На какую глубину он погрузится, если относительный вес бруса 0,7? Определить, сколько человек могут встать на брус, чтобы верхняя поверхность бруса оказалась бы заподлицо со свободной поверхностью воды, считая, что каждый человек в среднем имеет массу 67,5 кг.
Задача 1.23 Прямоугольная металлическая баржа длиной 60 м, шириной 8 м, высотой 3,5 м, загруженная песком, весит 14126 кН. Определить осадку баржи. Какой объем песка Vп нужно выгрузить, чтобы глубина погружения баржи была 1,2 м, если относительный удельный вес влажного песка равен 2,0?
Задача 1.24. Объемное водоизмещение подводной лодки 600 м3. С целью погружения лодки отсеки были заполнены морской водой в количестве 80 м3. Относительный удельный вес морской воды 1,025. Определить: какая часть объема лодки (в процентах) будет погружена в воду, если из подводной лодки удалить всю воду и она всплывет; чему равен вес подводной лодки без воды?
БУЛЫНИН,
ЦО № 17 ЦАО, г. Москва
Согласно школьной программе, законы
гидростатики изучаются лишь в 7-м классе,
возвращение к их изучению и закреплению в
дальнейшем не предусмотрено. Тем не менее задачи
на гидростатику относятся к весьма трудным и,
если в старших классах не было решено достаточно
подобных задач, то на вступительных экзаменах в
технические вузы ученик может столкнуться с
очень серьёзными, а то и непреодолимыми
трудностями. Предлагаемая подборка задач имеет
своей целью дать школьнику и преподавателю
физики представление об уровне сложности
материала по этой теме.
Задача 1 (МГТУ им. Н.Э.Баумана).
Плотность раствора соли с глубиной меняется по
закону
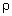
0 + Ah, где
В силу симметрии шариков относительно
горизонтальной плоскости, пороходящей через их
центры, сила Архимеда для каждого шарика равна
Объединяя все уравнения, находим:
Подставляя числовые данные, получаем:
Задача 2 (МГТУ им. Н.Э.Баумана).
В водоёме укреплена вертикальная труба с поршнем
так, что нижний конец её погружён в воду. Поршень,
лежавший вначале на поверхности воды, медленно
поднимают на высоту H = 15 м. Какую
работу пришлось на это затратить, если площадь
поршня 1 дм2, атмосферное давление p0 = 105 Па?
Массой поршня пренебречь.
Решение. Сила, которую надо
прикладывать к поршню, линейно возрастает от 0 до Fmax = p0S.
Зависимость этой силы от высоты столба поднятой
воды равна F(h) =
Максимально возможная высота столба
воды, поднятой таким способом, h1 = 10 м,
при этом
Подставив числовые данные, получаем A = 104 Дж.
Задача 3. Льдина площадью
1 м2 и толщиной 0,4 м плавает в воде.
Какую минимальную работу надо совершить, чтобы
полностью погрузить льдину в воду? Плотность
льда 900 кг/м3, g = 10 м/с2.
Решение. Пусть в исходном
состоянии h – глубина погружения плавающей
льдины. Запишем условие равновесия и следствия
из него:
л –
плотности воды и льда соответственно, Vпогр
– объём погружённой части льдины, V – её
полный объём, Н – толщина льдины, h –
толщина погружённой части.
При погружении льдины сила нажима
линейно возрастает от нуля до Fmax,
совершая работу
1-й способ. Разобьём работу на три
этапа:
– центр тяжести поднимается на высоту
– сила натяжения троса постоянна и
равна mg – FA;
(плотность бетона, по условию, в n
раз больше плотности воды).
– сила натяжения троса линейно
возрастает от mg – FA до mg, и
работа этой силы равна
– сила натяжения троса постоянна и
равна mg;
центр тяжести уже был поднят на
предыдущем этапе).
2-й способ. Применим закон
сохранения энергии. Работа равна изменению
энергии системы свая–вода. Потенциальная
энергия сваи возросла на mg(H + h).
Потенциальная энергия воды уменьшилась на
Задача 5 (МГТУ им. Н.Э.Баумана). В
сосуде находятся три несмешивающиеся жидкости
плотностями (сверху вниз)
. Толщина этих слоёв
Н/3, H и H соответственно. На дне
сосуда лежит стержень из материала плотностью 6
, массой m,
длиной H. Какую работу надо совершить,
поднимая стержень за один конец вертикально,
чтобы его верхний торец коснулся поверхности
жидкости плотностью
Пусть V – объём стержня, A1
– работа по подъёму стержня в жидкости
плотностью 3
сила линейно изменяется
от
A3 – работа по подъёму части
стержня длиной
(при этом нижний конец стержня и
соответственно центр тяжести этой части стержня
поднимается на
A4 – работа по перемещению
части стержня длиной
в жидкость плотностью
Полная работа равна:
Задача 6. Акселерометр
представляет собой изогнутую под прямым углом
трубку, заполненную маслом. Трубка располагается
в вертикальной плоскости, угол
Рассмотрим сосуд с жидкостью
(аквариум), который движется в горизонтальном
направлении с ускорением a. При
таком движении поверхность жидкости составляет
угол
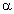
Такой же перепад высот имеет и
жидкость в трубке акселерометра, движущегося с
тем же ускорением. Получаем l = h2 + h1,
т.к., по условию,
Задача 7 (НГУ). Вертикальный
цилиндрический сосуд радиусом R, частично
заполненный жидкостью, вращается вместе с
жидкостью вокруг своей оси.
К боковой стенке сосуда на нити длиной l
привязан воздушный шарик радиусом r; во
время вращения нить образует со стенкой угол
Задача 8 (МГТУ им. Н.Э.Баумана).
Цилиндрический сосуд с жидкостью плотностью
вращается с
постоянной угловой скоростью
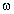
Направим ось X по направлению
стержня AB, а ось Y по вертикальной оси OO1.
По условию задачи, перемещение шара возможно
лишь вдоль стержня. Так как плотность шара меньше
плотности жидкости, составляющая силы Архимеда
вдоль оси X больше составляющей силы mgэфф,
и шар будет вытесняться жидкостью к оси вращения,
сжимая пружину. Исходное положение центра шара L0 + r.
Пусть во время вращения центр шара находится на
расстоянии x от оси, при этом пружина сжата
на величину L0 + r – x.
Уравнение движения шара массой m по
окружности радиусом x с угловой скоростью
имеет вид m
2x = Fц,
где сила Fц – результат сложения
горизонтальной составляющей силы Архимеда
Задача 9 (НГУ). Цилиндрический
космический корабль радиусом R вращается
вокруг своей оси с угловой скоростью
. Бассейн в корабле имеет
глубину H, а дном бассейна служит боковая
стенка корабля. Определите плотность плавающей в
бассейне палочки длиной l < H,
если из воды выступает её верхняя часть длиной
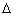
Во вращающейся неинерциальной системе
отсчёта роль силы тяжести играет центробежная
сила инерции Fц = m
Сила Архимеда, действующая на
погружённую часть палочки длиной l –
, равна FA
=
ж – плотность
жидкости (воды), S – площадь поперечного
сечения палочки.
Центр масс всей палочки находится от
оси вращения на расстоянии
Условие плавания палочки: P = FA,
где P – вес палочки.
Приравняв P и FА,
находим плотность палочки:
Вячеслав Леонидович Булынин окончил
физический факультет Ленинградского
государственного университета в 1964 г. и по 1992
г. работал в научно-исследовательских институтах
в области прикладной сверхпроводимости. С
1993 г. преподаёт в школе физику, астрономию,
математику; педагогический стаж 15 лет. Учитель
высшей квалификационной категории, методист ЦО
№ 17. Автор двух пособий по физике, изданных
«Континентом-Пресс» в 2004 г.: «Физика. Тесты и
задачи» и «Физика. Пособие для подготовки к
государственному экзамену». Женат, имеет двух
дочерей.
Урок посвящён решению задач по гидростатике об изменении уровня жидкости в сосуде. Рассматриваются два метода решения задач данного типа: через давление на дно и с использованием условия равновесия и закона Архимеда (через объёмы). Урок сопровождается компьютерной презентацией, в которой при решении задач используются статические модели в виде рисунков с фрагментарной анимацией.
- Образовательные:
учащиеся узнают способы решения задач по гидростатике об изменении уровня жидкости в сосуде и формулируют алгоритмы решения данного типа задач;учащиеся совершенствуют навыки решения задач об изменении уровня жидкости на дно сосуда; - учащиеся узнают способы решения задач по гидростатике об изменении уровня жидкости в сосуде и формулируют алгоритмы решения данного типа задач;
- учащиеся совершенствуют навыки решения задач об изменении уровня жидкости на дно сосуда;
- Развивающие:
формирование умения применять изученные алгоритмы к решению конкретных задач;формирование умения анализировать условие задачи и выбирать наиболее рациональный способ решения задачи;формирование познавательного интереса к физике посредством решения задач повышенной сложности и через использование информационных технологий; - формирование умения применять изученные алгоритмы к решению конкретных задач;
- формирование умения анализировать условие задачи и выбирать наиболее рациональный способ решения задачи;
- формирование познавательного интереса к физике посредством решения задач повышенной сложности и через использование информационных технологий;
- Воспитательные:
воспитание самостоятельности, любознательности;формирование коммуникативных навыков; - воспитание самостоятельности, любознательности;
- формирование коммуникативных навыков;
- персональный компьютер;
- проектор;
- интерактивная доска или экран;
- компьютерная презентация «Уровень жидкости в сосудах»,
- документ-камера.
- Организационный момент – 1 мин.
- Постановка целей и задач урока (создание проблемной ситуации) – 2 мин.
- Изучение нового материала (решение проблемной задачи) – 15 мин.
- Закрепление изложенного материала при решении задач – 23 мин.
Работа в группах – 15 мин.Презентация и защита – 8 мин. - Работа в группах – 15 мин.
- Презентация и защита – 8 мин.
- Подведение итогов – 3 мин.
- Организация домашнего задания – 1 мин.
Ход урока
- Гельгафт И.М., Генденштейн Л.Э., Кирик Л.А. 1001 задача по физике с решениями. Учебное пособие. – Харьков-Москва, 1995. – 592 с.
- Городские олимпиады по физике г. Нижнего Новгорода. 2004-2008 гг. Сборник задач. – Н.Новгород: Институт прикладной физики РАН, 2009. – 52 с.
- Подлесный Д.В. Анализ давления на дно сосуда в задачах гидростатики. // Потенциал, №10, 2005. – С. 42-45
- Полянский С.Е. Поурочные разработки по физике. – М.: ВАКО, 2004. –240 с.
- Черноуцан А. Гидростатика в стакане. // Квант, №3, 2008. – С. 47-50.
- Чивилёв В.И. Олимпиада «Физтех-2005». // Потенциал, №5, 2005. – С. 59-61.
Данные примеры задач, относятся к предмету «Гидравлика».
Задача #3321
Определить давление p1 в сечении 1-1 горизонтального расположенного сопла гидромотора, необходимое для придания скорости воде в выходном сечении 2-2 – V2 = 40 м/c, если скорость движения воды в сечении 1-1 – V1 = 3 м/c.
Задача #3322
Определить диаметр d суженной части горизонтального трубопровода, при котором вода поднимается на высоту h = 3,5 м (расход Q = 6 л/с, диаметр D = 10 см).
Задача #3323
Определить расход воды в горизонтальном трубопроводе переменного сечения, скорость на каждом из его участков и построить пьезометрическую линию, если H = 5 м, d1 = 15 мм, d2 = 20 мм и d3 = 10 мм.
Задача #3324
На водопроводной трубе диаметром d1, установлен водомер диаметром d2. На какую высоту h2 поднимается вода в пьезометрической трубке, установленной на узком сечении, при расходе воды Q, если уровень воды в пьезометре, присоединенном к основной трубе, h1? Потери напора не учитывать.
Задача #3331
По трубе диаметром d = 50 мм движется вода. Определить расход, при котором турбулентный режим движения сменится ламинарным, если температура воды t = 15 ℃.
Задача #3341
При ламинарном движении определить местную скорость на расстоянии r1 = 0,20 (d = 0,004 м) и r2 = 0,35 (d = 0,007) м от оси трубы, среднюю скорость, максимальную скорость и расход воды в трубе диаметром d = 0,020 м, если пьезометры, установленные на расстоянии l = 8,2 м друг от друга, показывают разность в отсчетах h = 0,01 м. Температура воды t = 10 ℃.
По результатам расчетов построить эпюру распределения скоростей по сечению трубы, задавшись масштабом скорости.
Задача #3342
Определить расход Q керосина (ρ = 800 кг/м3) в трубе диаметром D = 50 мм, если показание ртутного дифференциального манометра у сопла h = 175 мм, выходной диаметр сопла d = 30 мм, а его коэффициент сопротивления ζ = 0,08.
Какова потеря напора в расходомере?
При каком давлении перед соплом в расходомере начнется кавитация, если упругость паров керосина hн.п = 150 мм рт. ст.?
Задача #3343
К расходомеру Вентури присоединены два пьезометра и дифференциальный ртутный манометр. Выразить расход воды Q через размеры расходомера D и d, разность показаний пьезометров ΔH, а также через показание дифференциального манометра Δh. Дан коэффициент сопротивления ξ участка между сечениями 1-1 и 2-2.
Задача #3344
В трубопроводе диаметром d и длиной l под статическим напором H движется жидкость, кинематическая вязкость которой равна ν. Получить выражение для критического напора, при котором происходит смена ламинарного режима турбулентным, учитывая в трубопроводе только потери на трение.
Указание. Воспользоваться формулой для потерь на трение при ламинарном режиме:
H = (32νlv)/gd2,
имея в виде, что критический напор Hкр соответствует критической скорости vкр.
Задача #3381
Сравнить распределение в пласте в случаях установившейся плоскорадиальной фильтрации газа и несжимаемой жидкости по закону Дарси при одинаковых граничных условиях: rс = 0,1 м, pс = 50 кгс/см2, Rк = 750 м, pк = 100 кгс/см2.
Задача #338NaN
Круговая пластинка диаметром D, находясь под действием силы P, медленно опускается и выдавливает слой жидкости, динамическая вязкость которой равна μ.
Приняв течение жидкости ламинарным, определить закон нарастания усилия на пластине при движении ее с постоянной скоростью u0 по направлению к неподвижной плоскости.
Определить закон движения (путь – время), если сила P постоянна.
В течение каждого бесконечно малого промежутка времени рассматривать движение жидкости как установившееся.
Задача #3392
Кольцевая щель между двумя цилиндрами (D = 210 мм, d = 202 мм) залита трансформаторным маслом (ρ = 910 кг/м3) при температуре 20 ℃. Внутренний цилиндр равномерно вращается с частотой n = 120 мин –1. Определить динамическую и кинематическую вязкость масла, если момент, приложенный к внутреннему цилиндру, M = 0,065 Н × м, а высота столба жидкости в щели между цилиндрами h = 120 мм. Трением основания цилиндра о жидкость пренебречь.
Задача #3393
Определить силу, затрачиваемую на преодоление трения в подшипнике при вращении вала. Частота вращения вала n = 10 с–1. Диаметр шейки (цапфы) вала d = 40 мм, длина l = 100 мм, толщина слоя смазки между цапфой и подшипником δ = 0,2 мм. Кинематический коэффициент вязкости масла ν = 0,8 × 10–4 м2/с, плотность ρ = 980 кг/м3. Считать, что вал вращается в подшипнике соосно, а скорость движения жидкости в слое масла изменяется по линейному закону.
Задача #3394
Определить вес груза G ротационного вискозиметра, изображенного на рисунке. Диаметры: цилиндра Dц = 230 мм, барабана Dб = 228 мм, шкива d = 180 мм. Глубина погружения барабана в жидкость lб = 280 мм. Время опускания груза 8 с, путь lгр = 350 мм. В цилиндр залита жидкость плотностью ρ = 900 кг/м3, динамический коэффициент вязкости которой μ = 5,9 Па × с.







