- Энергия: что это такое
- Кинетическая и потенциальная энергии
- Закон сохранения механической энергии 🐲 спадило.ру
- Закон сохранения энергии в тепловых процессах
- Кинетическая энергия
- Механическая энергия
- Переход механической энергии во внутреннюю
- Потенциальная энергия
- Установим связь между работой и энергией. по второму закону ньютона
Энергия: что это такое
Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
Кинетическая и потенциальная энергии
Энергия является одной из важнейших характеристик системы материальных
точек. Понятие энергии используется не только в физике, но и в других
естественных науках: химии, биологии, технических науках и пр. При движении
системы ее энергия может меняться и принимать различные формы. Между работой и
энергией существует глубокая связь.
Энергией называется физическая величина, характеризующая способность тела
совершать работу. Энергия – универсальная мера различных форм движений и
взаимодействий. В зависимости от вида движения можно выделить механическую,
тепловую, электромагнитную, атомную и другие виды энергии.
Рассмотрим механическую энергию и свяжем изменение энергии с работой,
производимой над материальной точкой. В механике энергию разделяют на кинетическую
и потенциальную. Первая характеризует движение тела и зависит от
скорости, а вторая – запасенную энергию и зависит от положения тела.
Закон сохранения механической энергии 🐲 спадило.ру
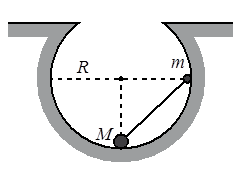 Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.
Небольшие шарики, массы которых m = 30 г и M = 60 г, соединены лёгким стержнем и помещены в гладкую сферическую выемку.
В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Максимальная высота подъёма шарика массой М относительно нижней точки выемки оказалась равной 12 см. Каков радиус выемки R?
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж конечного положения шариков. Обозначить их высоты, выбрать нулевой уровень отсчета потенциальной энергии. Выбрать систему координат.
3.Записать закон сохранения энергии.
4.Выполнить общее решение задачи.
5.Подставить известные данные и выполнить вычисление искомой величины.
Решение
Запишем исходные величины:
• Масса первого шарика: m = 30 г.
• Масса второго шарика: M = 60 г.
• Максимальная высота подъема шарика М: H = 12 см.
Переведем единицы измерения величин в СИ:
30 г = 0,03 кг
60 г = 0,06 кг
12 см = 0,12 м
Выполним чертеж:
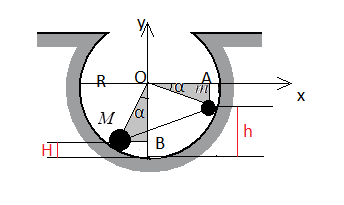
Нулевой уровень — нижняя точка выемки.
Запишем закон сохранения энергии:
Ek0 Ep0 = Ek Ep = const
В начальном положении кинетическая энергия обоих шариков равна 0. Потенциальная энергия шарика М тоже равна нулю, так как он находится на нулевом уровне. Потенциальная энергия шарика m равна:
Ep0m = mgR
Кинетическая энергия шариков после установления равновесия тоже будет равна нулю. Но b[ потенциальная энергия будет отличной от нуля:
Epm = mgh
EpM = MgH
Поэтому закон сохранения энергии применительно к задаче примет вид:
mgR = mgh MgH
Преобразуем выражение и получим:
mgR−mgh=MgH
R−h=MgHmg..=MHm..
При движении гантели по поверхности выемки высоты подъема большого и малого шаров связаны. Рассмотрим прямоугольные треугольники OmA и OMB. Для них справедливы следующие равенства:
MB = mA = R – h
OA = OB = R – H
OM = Om = R
Это дает нам право воспользоваться теоремой Пифагора:
(R−h)2=R2−OA2=R2−(R−H)2
Следовательно:
(R−h)2=R2−(R2−2RH H2)=2RH−H2
Подставим в это выражение правую часть ранее полученного выражения:.
R−h=MHm..
(MHm..)2=2RH−H2
Теперь можем выразить и вычислить радиус:
2RH=(MHm..)2 H2
R=(MHm..)2 H22H..
R=(Mm..)2H2.. H2..=(0,060,03..)20,122.. 0,122..=0,3 (м)
.
.
Ответ: 0,3
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия. |
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом. |
Математически его можно описать так:
Уравнение теплового баланса Q отд = Q пол Qотд — отданное системой количество теплоты [Дж] Q пол — полученное системой количество теплоты [Дж] |
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9·10^7Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг·°С).
Решение:
При нагревании тело получает количество теплоты
Q = cmΔt ,
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
Qсгор = q*mсгор,
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание пошло 20% затраченной энергии.
То есть:
Q = 0,2 * Qсгор
cmΔt =0,2 * qmсгор
mсгор = cmΔt / 0,2 q
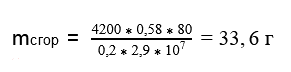
Ответ: масса сгоревшего топливаа равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг*℃, удельная теплота плавления льда равна 3,3*10^5 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = cmΔt
Qнагрев = 2100 * 0,5 * (10-0) = 10500 Дж
Для превращения льда в воду:
Qпл = λm
Qпл = 3,3 * 10^5 * 0,5 = 165000 Дж
Таким образом:
Q = Qнагрев Qпл = 10500 165000 = 175500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия Ек = (m*v^2)/2 Ек — кинетическая энергия [Дж] m — масса тела [кг] v — скорость [м/с] |
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 килограмм, если она бежала за мячом с постоянной скоростью 2 м/с.
Решение:
Формула кинетической энергии Ек = (m*v^2)/2
Подставляем значения
Ек = (10*2^2)/2 = 20 Дж
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 килограммам, а его кинетическая энергия — 40 Дж
Решение:
Формула кинетической энергии Ек = (m*v^2)/2
Выразим скорость:
v^2 = (2*Eк)/m
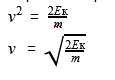
Подставляем значения
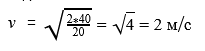
Ответ: гном бежал со скоростью 2 м/с.
Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим 😂), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Задачка
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
Решение:
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 Евнутр
Емех = Емех/2 Евнутр
Емех/2 = Евнутр
Евнутр = Ек/2
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины Еп = (k*x^2)/2 Еп — потенциальная энергия [Дж] k — жесткость [Н/м] x — удлинение пружины [м] |
Потенциальная энергия Еп = mgh Еп — потенциальная энергия [Дж] m — масса тела [кг] g — ускорение свободного падения [м/с^2] h — высота [м] На планете Земля g ≃ 9,8 м/с^2 |
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с^2.
Решение:
Формула потенциальной энергии Еп = mgh
Подставляем значения
Eп = 0,1 * 9,8 * 2500=2450 Дж
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 килограмм, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с^2.
Решение:
Формула потенциальной энергии Еп = mgh
Выразим высоту:
h = Eп/mg
Переведем 637 кДж в Джоули.
637 кДж = 637000 Дж
Подставляем значения
h = 637 000/(65 * 9,8) = 1000 м
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:
Потенциальная энергия вычисляется по формуле: E = mgh
По условию задачи
m1 = m
h1 = 2h
m2 = 2m
h2 = h
Таким образом, получим, что
E1 = m*g*2h = 2 mgh,
а E2 = 2mgh,
то есть E1 = E2.
Ответ: E1 = E2.
Установим
связь между работой и энергией. по второму закону ньютона
Умножим
обе части на ds = vdt и выполним ряд простейших
преобразований:
Кинетической
энергиейматериальной точки называется выражение
Учитывая,
что dA = Fds,
получим
Следовательно,
изменение кинетической энергии материальной точки равно работе, произведенной
над этой точкой.
Потенциальной
энергией называется механическая
энергия материальной точки, определяемая положением этой точки и характером сил
взаимодействия этой точки с другими телами и окружающими полями.
Потенциальная
энергия обычно является функцией координат U=U(r). Полная энергия
материальной точки представляет собой сумму кинетической и потенциальной
энергий:
Потенциальную
энергию можно рассматривать как запасенную энергию, которую можно превратить в
работу. Например, поднятый на высоту h груз
обладает потенциальной энергией
где
g=9,81 ![]() A
A
= U. Если работа не совершается, то потенциальная энергия
при опускании груза может превратиться в кинетическую:
Потенциальная
энергия может храниться в виде некоторого поля, которое называют потенциальным
или силовым. Типы полей: гравитационное, электрическое, магнитное,
ядерных сил и др.
Поле
называется потенциальным, если работа, совершаемая при перемещении тела
из точки А в точку В, не зависит от траектории, а определяется начальным и
конечным значениями точек.
Силы,
действующие в потенциальном поле, называются консервативными. Работа в
потенциальном поле определяется выражением
т.е.
работа выполняется за счет уменьшения потенциальной энергии.
Если
потенциальная энергия зависит от координат, то полный дифференциал dU
определяется формулой
Вектор
называется
градиентом потенциального поля. Между силой и градиентом поля существует
связь
F= – gradU.
Следовательно,
зная зависимость потенциальной энергии от координат, легко определить силу в
любой точке пространства.
Используя законы Ньютона, можно доказать закон сохранения энергии для
механических систем.
Закон сохранения энергии.В механических системах, где действуют только
консервативные силы, полная энергия системы сохраняется:
Если
в системе действуют неконсервативные силы, то механическая энергия системы
может изменяться, превращаясь в другие виды (тепловую, химическую и т.д.). В
более широком смысле, если рассматривать все возможные виды энергии, то полная
энергия замкнутой системы всегда сохраняется.
3. Закон сохранения импульса
работа энергия импульс сохранение
Часто приходится иметь дело с совокупностью многих тел, взаимодействующих
между собой. Механической системой называется совокупность материальных
точек, рассматриваемых как единое целое. Сформулируем простейшие понятия,
необходимые для описания механических систем.
Внутренними силами называются силы взаимодействия между материальными точками
механической системы.
Внешними силами называются силы, с которыми на материальные точки
механической системы действуют внешние тела.
Механическая система называется замкнутой, если на нее не
действуют внешние силы или их равнодействующая равна нулю.
Центром масс механической системы называется точка, положение которой
определяется выражением
где
![]()
![]()
![]()
Закон сохранения импульса: Импульс замкнутой системы сохраняется:
P=![]()
4.
Использование законов сохранения
Использование
законов сохранения позволяет описать многие процессы, происходящие в природе,
часто даже не зная многих деталей этих процессов. Благодаря использованию
законов сохранения были получены многие соотношения в молекулярной физике,
предсказаны новые элементарные частицы, открыты новые типы взаимодействий.
Пример 1. На какую высоту поднимется тело, брошенное
вертикально вверх с начальной скоростью ![]()
Первое решение (кинематическое). В верхней точке
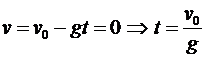 h.
h.
Второе
решение (энергетическое). Из закона
сохранения энергии
Пример 2. По шероховатой горизонтальной плоскости с
коэффициентом трения k скользит шайба. Какое расстояние она пройдет, если
начальная скорость шайбы ![]()
Первое решение (динамическое).
Сила
трения ![]()
Следовательно
В
конце пути
Пройденный
путь
Второе
решение (энергетическое).
Кинетическая энергия расходуется на совершение работы:
Из
приведенных примеров видно, что использование законов сохранения энергии
позволяет получить решение задачи более простым путем.
.
Столкновение двух тел
Законы
сохранения энергии и импульса удобно использовать при решении задач
столкновения двух тел. При этом можно ничего не знать о механизме самого
столкновения, когда изменяются скорости тел, могут меняться массы и форма тел.
В решении задачи участвуют начальные и конечные массы и скорости тел.
Рассмотрим
центральный удар двух шаров. Удар называется центральным, если тела до
удара движутся вдоль прямой, проходящей через их центры масс. Для простоты
рассмотрим центральный удар двух шаров.
Рис. 1
Здесь
предполагается, что ![]()
Абсолютно
упругим называется такой удар, при
котором механическая энергия тел не переходит в другие виды энергии.
Абсолютно
неупругим называется такой удар,
после которого тела объединяются (слипаются).
В
общем случае удар, как правило, не является ни абсолютно упругим, ни абсолютно
неупругим. Тела могут после удара разлететься, но часть их кинетической энергии
может перейти в тепловую энергию или энергию деформации.
Используя
законы сохранения, опишем абсолютно упругий и абсолютно неупругий удары.
Абсолютно
неупругий удар. Движение шаров до
удара происходит так, как показано на Рис.1. Движение шаров после удара
показано на Рис.2.
Рис.
2.
Из
закона сохранения импульса
При
абсолютно неупругом ударе энергия тела не сохраняется.
Абсолютно
упругий удар. Движение шаров до удара
происходит так, как показано на Рис. 1. Движение шаров после удара показано на
Рис. 3.
Рис. 3.
(если
направления скоростей угаданы неправильно, то вычисленные значения скорости
получатся со знаком минус). Запишем законы сохранения импульса и энергии
Решая
эту систему уравнений относительно ![]()
![]()
Рассмотрим
некоторые частные случаи:
) т1
= т2. Получим
т.е.
шары меняются скоростями. В частности, если ![]()
![]()
Полученные
формулы можно использовать не только при центральном ударе шаров, но и во
многих других случаях, когда выполняются условия, сформулированные при решении
задачи.
1. Работа силы
2. Мощность
3. Кинетическая энергия
4. Потенциальная энергия тела, поднятого на высоту h
5. Координаты центра масс
6. Скорость тел при абсолютно неупругом ударе
7. Скорости тел при абсолютно упругом ударе
Список использованной литературы и источников
1. Трофимова Т.И. Курс физики, М.: Высшая школа, 1998, 478 с.
. Трофимова Т.И. Сборник задач по курсу физики, М.: Высшая
школа, 1996, 304с
. Волькенштейн В.С. Сборник задач по общему курсу физики,
СПб.: «Специальная литература», 1999, 328 с.
. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики
с решениями, М.: Высшая школа, 1999, 592 с.
. Все решения к «Сборнику задач по общему курсу физики» В.С.
Волькенштейн, М.: Аст, 1999, книга 1, 430 с., книга 2, 588 с.
. Красильников О.М. Физика. Методическое руководство по
обработке результатов наблюдений. М.: МИСиС, 2002, 29 с.
. Супрун И.Т., Абрамова С.С. Физика. Методические указания по
выполнению лабораторных работ, Электросталь: ЭПИ МИСиС, 2004, 54 с.







