Дополнительные упражнения для вратарей
ОБУЧЕНИЕ ТЕХНИКЕ ИГРЫ ВРАТАРЯ
В мини-футболе вратарь – фигура особая. Команде, имеющей в своем составе полевых игроков хорошего уровня, но плохо подготовленного стража ворот, очень трудно добиться успеха. И наоборот. Средняя по подбору игроков команда, но с надежным вратарем способна на многое. Никто, конечно, не возьмет на себя смелость определить, с какого возраста готовиться на амплуа вратаря. Одни уже в младшем возрасте мечтают играть в воротах, другие выбирают «должность» стража ворот, уже попробовав свои силы в роли полевого игрока.
Практика показывает, что в мини-футболе более эффективно действуют те вратари, которые быстро и экономно перемещаются по площадке. Вот почему игрокам этого амплуа необходимо научиться резко стартовать, неожиданно изменять направление движения, свободно передвигаться лицом и спиной вперед, приставными шагами боком и спиной, совершать разнообразные прыжки и делать внезапные остановки. Естественно, все эти приемы неразрывно связаны между собой и, как правило, выполняются из самых различных стартовых положений.
В мини-футболе вратарь в зависимости от места нахождения мяча использует несколько вариантов стойки . В случаях, когда соперник с мячом находится прямо против ворот, но на некотором расстоянии от них, вратарь занимает позицию в середине ворот. Его ноги чуть согнуты и расставлены на ширину плеч, вес тела равномерно распределен на обе ноги, а туловище немного наклонено вперед. Такая позиция является основной стойкой вратаря (рис.1 а). Если же соперник с мячом сближается с воротами, стойка вратаря претерпевает изменение. Она становится более низкой, а туловище больше наклоняется вперед. Вес тела вратаря сильнее переносится на переднюю часть стоп (рис.1 б).
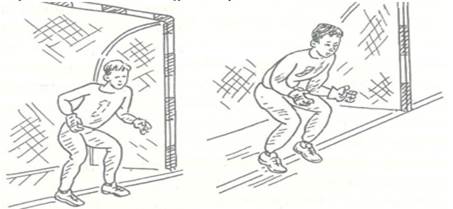
а б
Рисунок 1 – Варианты стойки вратаря если соперник находится прямо против ворот
Когда соперник с мячом двигается по флангу, вратарь занимает позицию вплотную к ближней стойке ворот. Ближняя к стойке рука вытягивается вверх, прикрывая верхний угол, другая рука отводится в сторону, страхуя незащищенное пространство. Вес тела вратарь переносит на стоящую у стойки ногу (рис.2). В такой позиции страж ворот имеет возможность отразить мячи, летящие на него на любой высоте, а также отбить ногой или рукой мячи, посылаемые соперниками в сторону дальней стойки ворот.
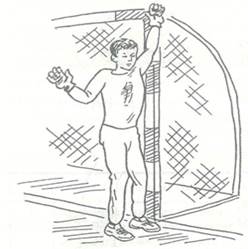
Рисунок 2 – Стояка вратаря если соперник мячом двигается по флангу
Наряду с ловлей мяча вратарю в мини- футболе приходится отбивать мячи руками и ногами, выполнять падения и броски в ноги атакующему сопернику или на отскочивший от игроков мяч. Овладев мячом, вратарь должен быстро и точно довести его до партнера.
Естественно, овладение юными вратарями данным арсеналом технических приемов возможно только при условии систематических занятий и постоянного анализа своих действий.
Особенности техники и технической подготовки вратарей.
Ловля мячей.
Ловля катящихся и низколетящих на вратаря мячей осуществляется при параллельном расположении стоп (рис.3). Взгляд вратаря устремлен на приближающийся мяч. Когда мяч оказывается рядом, вратарь смыкает ноги и затем наклоняется вперед. При этом ноги сгибаются в коленях. Подхватив мяч опущенными вниз кистями, вратарь выпрямляется и прижимает мяч к груди. Если же мяч движется на расстоянии шага в стороне от вратаря, он одновременно с наклоном к мячу делает шаг ближней ногой и еще до касания мяча руками приставляет к ней другую ногу. Данный технический прием основан на хорошей “работе” ног и внимательном наблюдении за движением мяча. В то же время вратарь должен учитывать, что при неожиданном отклонении мяча, при скученности игроков перед воротами нередко использование этого приема может быть чревато проблемами.
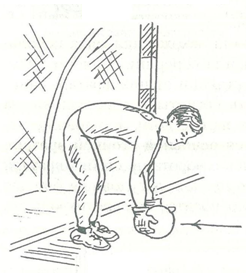
Рисунок 3 – Ловля катящихся и низколетящих на вратаря мячей осуществляется при параллельном расположении стоп
Для большей надежности ловлю катящихся на вратаря мячей рекомендуется осуществлять в стойке на одном колене (рис.4). При приближении мяча вратарь переносит вес тела на сильно согнутую в коленном суставе опорную ногу. Другая нога разворачивается наружу и опускается на колено около опорной ноги. Ее голень становится поперек, словно барьер на пути мяча. Руки вратаря, опущенные вниз, почти касаются поверхности площадки между его ногами. Соприкоснувшись с коленями, мяч прокатывается по предплечьям и прижимается к груди или животу.
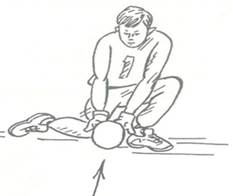
Рисунок 4 – Ловля катящихся на вратаря мячей
Тренировочные упражнения
1. Из стойки ноги врозь выполните наклоны вперед, не сгибая ноги в коленях, с касанием поверхности площадки ладонями. Вариант: то же, но наклоны выполняются из стойки ноги вместе ит.д.
2. Из основной стойки вратаря выполните наклоны вперед, захватите лежащий перед вами мяч и подтяните его к груди ит.д.
3. Занимающиеся упражняются в парах. Один из игроков, приняв основную стойку вратаря, при приближении мяча, который ему накатывает партнер с 3-4 шагов, наклоняется и подхватывает мяч ладонями. Выпрямившись, он прижимает мяч к груди. Теперь уже второй игрок принимает основную стойку вратаря, а партнер накатывает ему мяч ит.д.
4. Занимающиеся выстраиваются в колонну по одному. Стоящий перед колонной игрок накатывает мяч на головного игрока, который принимает основную стойку вратаря, наклоняется и ловит мяч. Затем ударом ногой он направляет мяч низом обратно, а сам перебегает в конец колонны ит.д.
5. Занимающиеся упражняются в парах. Один из них занимает место в воротах, а его партнер с 5-6 шагов несильным ударом посылает на него мячи низом. Задача вратаря – продемонстрировать правильную технику приема мяча. Вариант: то же, но мяч направляется чуть правее или левее от вратаря, который, сделав шаг в сторону, соединяет ноги и ловит мяч.
6. Упражняются три игрока. Двое из них встают друг против друга на расстоянии 16-18 шагов и поочередно ударом ногой направляют мячи низом вратарю, который занимает позицию между ними. Вратарь ловит мячи, стоя на месте или сделав движение в сторону. Овладев мячом, вратарь возвращает его тому же игроку, поворачивается кругом и принимает мяч от другого игрока. Периодически партнеры меняются ролями свратарем.
7. Несколько игроков встают в 8-12 шагах от ворот и ударом ногой с разной силой поочередно направляют мячи низом в сторону от вратаря.
Ловля катящихся и низколетящих в стороне от вратаря мячей выполняется в падении и броске (рис.5). Уловив направление движения мяча, вратарь, используя падение, как бы стелется по поверхности площадки. При этом он последовательно касается поверхности поля голенью, бедром, тазом и рукой. Мяч захватывается одной рукой сзади, другой – сверху и подтягивается к груди. Техника приема мяча в броске отличается фазой полета в направлении движущегося в ворота мяча.
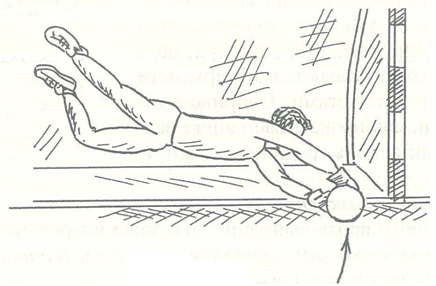
Рисунок 5 – Ловля катящихся и низколетящих в стороне от вратаря мячей
Ловля мяча в падении или броске в мини-футболе часто применяется и после выхода вратаря из ворот на атакующего соперника (рис.6). Вратарь должен принять мгновенное решение, точно определив, что сможет раньше соперника или хотя бы одновременно с ним достать мяч, предотвратив этим опасный момент. Оценив таким образом ситуацию, он делает несколько шагов вперед и в падении или броске овладевает мячом, отпущенным атакующим слишком далеко от себя, или же, сближаясь с соперником, он своим телом преграждает путь мячу в ворота (рис.7).
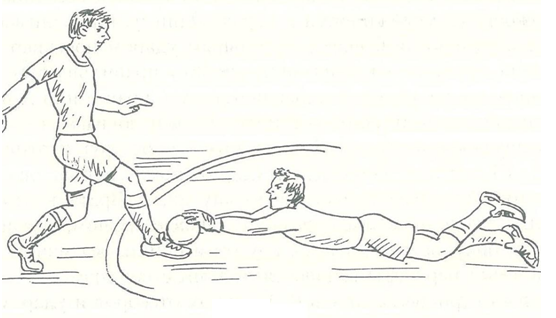
Рисунок 6 – Ловля мяча в падении или броске в мини-футболе часто применяется и после выхода вратаря из ворот на атакующего соперника
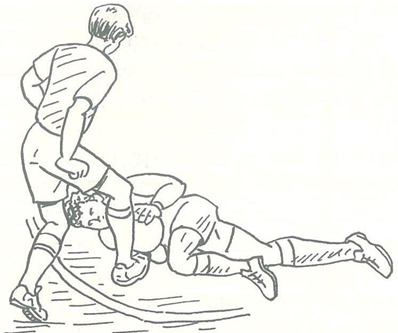
Рисунок 7 -Ловля мяча в падении или броске в мини-футболе часто применяется и после выхода вратаря из ворот на атакующего соперника
Аналогичный прием используется вратарем в мини- футболе и в тех случаях, когда кто-то из соперников низом направляет мяч в штрафную площадь одному из своих партнеров. Задача: оценив ситуацию, быстро выйти из ворот и в падении или броске овладеть мячом или отбить его в поле.
Тренировочные упражнения
1. Вратарь опускается на колени, держа мяч в руках. По первому сигналу партнера он выполняет падение на левый бок, вытянув руки с мячом. По второму сигналу вновь занимает исходное положение. Далее упражнение выполняется в другую сторону и т.д.
2. Вратарь занимает позицию стоя на коленях. Справа и слева от него кладется по мячу. Вратарь поочередно то в одну, то в другую сторону выполняет падение на мяч. Захватив мяч руками, он подтягивает его к груди.
3. Вратарь занимает позицию присев. Справа и слева от него кладется по мячу. Вратарь поочереднотоводну,товдругуюсторонувыполняетпадениенамячспоследующим быстрым вставанием. Вариант: а) то же, но упражнение выполняется из основной стойки вратаря; б) то же, но бросок выполняется сквозь обруч.
4. Занимающиеся упражняются в парах. Один из них ударом ногой посылает мяч низом так, чтобы он проходил в 1-1,5 шагах от партнера. Тот броском из основной стойки овладевает мячом с последующим быстрым вставанием. После этого он направляет мяч ударом ногой низом мимо своего товарища ит.д.
5. Вратарь ложится на бок у ворот грудью к партнеру. Тот с расстояния 6-7 шагов накатывает ему мяч низом так, чтобы он двигался в сторону от вратаря. Оттолкнувшись туловищем и бедром от поверхности площадки, вратарь стремится поймать мяч. После этого он возвращается в исходную позицию и т.д. Постепенно упражнение усложняется. Партнер накатывает мяч все дальше от вратаря или же увеличивает силу удара по мячу.
6. Вратари занимаются в парах. Они садятся напротив друг друга на расстоянии 2-3 шага. Вратарь, имеющий мяч, бросает его в сторону партнера на высоте около 0,5 м так, чтобы последний в броске из положения сидя ловил мяч. Поймав мяч, тот таким же образом бросает его партнеру. Мячи направляются вправо или влево от партнера на расстоянии примерно 1м.
7. Занимающиеся упражняются в парах. Один из них становится с мячом напротив партнера, который занимает позицию, опустившись на одно колено. Первый набрасывает мяч в сторону от партнера так, чтобы он проходил мимо него на высоте около 0,5 м. Поймав мяч в падении или броске, партнер возвращает мяч назад и т.д. Мяч направляется в сторону той ноги, на колено которой опустился партнер. Его задача – при приземлении использовать наиболее мягкую часть тела. Через некоторое время партнер меняет позицию, опускаясь уже на другую ногу. Периодически игроки меняются ролями.
8. В 8-10 м от ворот (параллельно линии ворот) в ряд устанавливается 8-10 мячей. Несколько игроков один за другим (с некоторой паузой) наносят удары по воротам так, чтобы мяч летел на небольшой высоте или низом в стороне от вратаря. Последний старается в падении или броске овладеть мячом. Первую серию ударов игроки выполняют с одного конца установленного ряда мячей, а следующую – с другого конца ит.д.
9. Занимающиеся упражняются в тройках. Один из них встает в ворота, слева и справа от которых из стоек сооружаются малые ворота. В 5-6 шагах перед этими воротами встают партнеры вратаря. Они поочередно несильными ударами низом посылают мячи в малые ворота. Вратарь должен из основной стойки в стелющемся броске овладеть мячом. Поймав мяч, он быстро возвращает его обратно и занимает исходную позицию. Теперь уже он выполняет бросок в другую сторону и т.д. Периодически партнеры меняются ролью с вратарем.
10. Вратарь занимает позицию в середине ворот. В 1,5 шагах от него кладется набивной мяч. Его партнер встает сбоку и бросает на небольшой высоте мяч так, чтобы вратарь, выбежав из ворот, в броске через набивной мяч овладел им. Через некоторые время мячи бросаются с другой стороны ворот ит.д.
11. Упражняются два игрока. Один из них занимает место в воротах. Его партнер, встав в 2-3 шагах от первого, бросает в сторону от него мяч так, чтобы тот отскакивал от площадки на высоту до 0,5 м. Игрок, занявший позицию в воротах, оттолкнувшись, в броске ловит отскочивший мяч. Мяч направляется то в одну, то в другую сторону от вратаря. Периодически партнеры меняются ролями.
12. Упражняются два игрока. Один из них занимает позицию в середине ворот спиной к партнеру. Тот стоит с мячом в трех метрах от линии ворот. По звуковому сигналу вратарь разворачивается на 180° и в броске ловит отскочивший от площадки мяч, который его партнер броском направляет в площадку (в сторону от вратаря). Периодически игроки меняются ролями.
13. Вратарь занимает место в середине ворот и бросает мяч в направлении стойки. После отскока мяча от площадки он, оттолкнувшись, в броске ловит мяч.
14. Вратарь занимает место в воротах. В 12 шагах от ворот встают с мячами несколько игроков. Они поочередно проходят к воротам, преднамеренно несколько отпуская от себя мяч на границе штрафной площади. Задача вратаря -выбежать навстречу атакующему и в падении или броске овладеть мячом как можно ближе к линии штрафной площади. Вариант: то же, но, войдя в штрафную площадь, игроки стараются обыграть вратаря и забить мяч в ворота.
15. Вратарь занимает позицию в центре ворот спиной к 6-метровой отметке. У той и другой стойки ворот встают с мячами два игрока, лицом к той же отметке. Они поочередно ударом ногой направляют мячи низом вперед, предварительно подав вратарю звуковой сигнал. Развернувшись на 180°, вратарь делает два-три шага вперед и в броске ловит уходящий мяч, стараясь, чтобы он не пересек границу штрафной площади, ит.д.
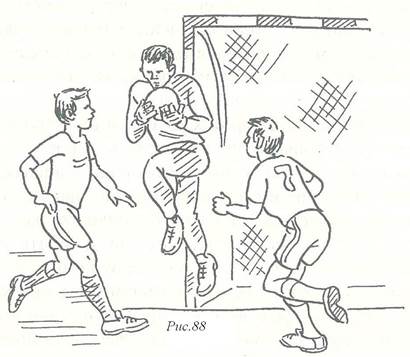Ловля полу высоких мячей, т.е. летящих на вратаря выше колен и ниже головы, осуществляется на месте (рис.8) или в прыжке. При приближении с мячом сгибает коленные суставы и сближает ноги, подав вперед верхнюю часть туловища. При этом «угол» между туловищем и бедрами образует своеобразное ложе для мяча. Руки, согнутые в локтях, выдвигаются вперед, ладонями к мячу. Мяч прокатывается последовательно по ладоням, предплечьям и прижимается к туловищу. Если вратарь в момент ловли мяча находится в положении шага, то в целях уменьшения силы удара вес тела переносится на сзади стоящую ногу.
Рисунок 8 – Ловля полу высоких мячей, т.е. летящих на вратаря выше колен и ниже головы
Ловля в прыжке выполняется в целях опережения соперников, готовых овладеть мячом, летящим примерно на уровне груди вратаря. Сделав один-два шага и оттолкнувшись одной ногой от площадки, вратарь в прыжке принимает мяч на грудь, прижимая его руками (рис.9).
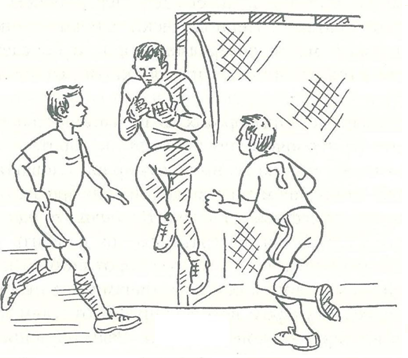
Рисунок 9 – Ловля в прыжке
Тренировочные упражнения
1. Встав в положение ноги чуть шире плеч, с согнутыми в локтях и вытянутыми вперед руками (мяч на ладонях), вратарь подтягивает его к груди и вновь возвращает в исходное положение и т.д. 2. Из той же позиции вратарь подбрасывает мяч на 30-40 см, ловит его и подтягивает к груди.
3. Стоя в воротах, вратарь ловит мячи, набрасываемые партнером с 2- 3 шагов, на уровне живота.
4. Вратарь занимает позицию в середине ворот. Несколько игроков поочередно набрасывают с 6-7 шагов ему мячи так, чтобы они летели над уровнем живота. При этом мячи должны несколько не долетать до вратаря, задача которого – сделать рывок и овладеть мячом. Вариант: то же, но мяч на вратаря посылается ударом ногой с 8-10 шагов. Вратарь занимает позицию в середине ворот. Партнеры поочередно набрасывают мячи с расстояния 7-8 шагов то в одну, то в другую сторону от вратаря. Его задача – переместившись в соответствующую сторону приставными или скрестными шагами, поймать мяч.
5. Несколько игроков, расположившись по дуге в 8-10 шагах от ворот, поочередно ударом ногой с разной силой посылают мячи на уровне живота или груди в сторону вратаря. Последний ловит летящие мячи, стоя на месте, в прыжке в сторону и вперед.
6. Вратарь занимает место в воротах. В 2-3 м перед воротами ставится набивной мяч. Партнеры с 8-9 шагов набрасывают мячи так, чтобы вратарь, выбежав из ворот, ловил мяч в прыжке над набивным мячом.
7. Вратарь занимает позицию лицом к стенке на расстоянии 2 м. Позади него и чуть сбоку располагаются два игрока с мячами. Они поочередно выполняют броски мячей в стенку. Вратарь ловит отскочившие от стенки мячи на уровне груди, стоя на месте или в прыжке.
Ловля высоколетящих на вратаря (или рядом с ним) мячей выполняется как на месте, так и в прыжке. При ловле на месте, т.е. в опорном положении (рис.83), при приближении летящего мяча руки вратаря вытягиваются вверх, ладони обращаются к мячу, большие пальцы почти соприкасаются. Пойманный мяч мягким движением переносится на грудь или же в исходное положение для вбрасывания партнеру. В момент ловли мышцы рук должны быть расслабленными, амортизируя таким образом силу удара. Если вратарь напрягает кисти, мяч может отскочить от рук и стать добычей соперников.
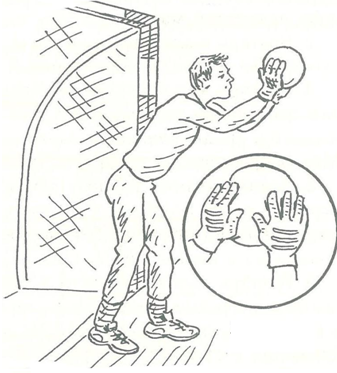
Рисунок 10 – Ловля высоколетящих на вратаря
Ловля высоколетящих мячей в прыжке выполняется толчком одной или двумя ногами с места (рис.11) или с разбега. Таким образом, как правило, вратари осуществляют ловлю опускающихся в штрафную площадь мячей. Приземляется вратарь в основном в положение ноги врозь, что позволяет мгновенно ввести мяч в игру.
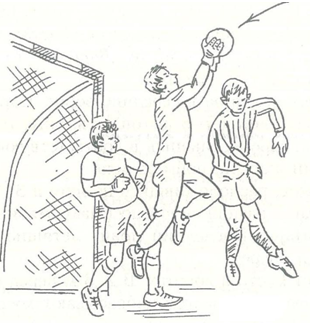
Рисунок 11 – Ловля высоколетящих мячей в прыжке
Тренировочные упражнения
1. Вратарь держит мяч на уровне лица так, чтобы большие пальцы рук почти соприкасались. По сигналу партнера он отводит назад кисти рук (как бы выпуская мяч) и тут же вновь возвращает их в исходное положение, словно ловя падающий мяч.
2. Вратарь набрасывает мяч над головой, а затем, поймав, опускает и заключает его в «угол», образованный предплечьями и грудью.
3. Вратари упражняются в парах. Встав в двух шагах друг против друга, они поочередно подбрасывают мяч над партнером, который ловит его и прижимает к груди. Вариант: партнеры встают в 5-6 шагах друг против друга. Мяч набрасывается по крутой траектории.
4. Занимающиеся располагаются по кругу в положении присев. Один из игроков, заняв позицию в центре круга, подбрасывает мяч вверх и называет имя одного из игроков. Тот быстро встает, делает два-три шага и в прыжке ловит мяч в наивысшей точке.
5. Вратарь занимает место в середине ворот. Несколько игроков с 8-12 шагов поочередно ударом с полулѐта по высокой траектории направляют мячи в штрафную площадь так, чтобы вратарь выполнял ловлю в прыжке после движения в сторону и вперед.
6. Данное упражнение выполняется так же, как и предыдущее. Но вратарь выполняет ловлю в борьбе с одним из игроков, который вначале действует пассивно.
7. Вратарь занимает позицию в середине ворот. Его партнер встает на 10-метровой отметке и по высокой траектории набрасывает мячи так, чтобы они опускались в штрафную площадь около самой ее границы. Вратарь выбегает вперед и в прыжке выполняет ловлю мяча в наивысшей точке. Внимание вратаря акцентируется на том, чтобы прыжок вверх был строго вертикальным и при приземлении он не переступал линию штрафной площади. Периодически партнеры меняются ролями.
8. Вратарь располагается в середине ворот, приняв основную стойку. Позади ворот встают с мячами два игрока. Они поочередно через перекладину набрасывают мячи по высокой траектории так, чтобы они опускались примерно в 1-2 шагах перед границей штрафной площади. Вратарь, которому мяч в такой ситуации попадает в поле зрения с опозданием, должен проявить необходимую реакцию. Заметив мяч, он резко стартует и в прыжке ловит мяч в наивысшей точке.
9. Вратарь занимает позицию у стойки ворот, касаясь ее рукой. В 5 м от него встает его партнер. Он набрасывает мяч верхом в противоположный угол ворот. Вратарь, переместившись туда приставными шагами боком, в прыжке ловит мяч в наивысшей точке. Затем упражнение повторяется таким же образом в другую сторону. Периодически партнеры меняются ролями.
Ловля полувысоких и высоких мячей, летящих в стороне от вратаря, вы-полняется в броске. Этот прием, как правило, применяется, когда соперники наносят сильные удары по воротам. Вратарь энергично отталкивается от площадки вверх-в сторону. Руки его поднимаются вверх, ладонями к мячу. Пальцы слегка разводятся, создавая этим большую площадь для приема мяча (рис.12). В момент ловли руки вратаря сгибаются и подтягивают мяч к груди. При приземлении вратарь группируется.
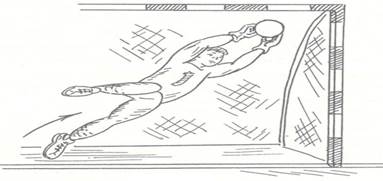
Рисунок 12 – Ловля полувысоких и высоких мячей в броске
Тренировочные упражнения
1. Занимающиеся упражняются в парах. Один из игроков принимает основную стойку вратаря. Другой встает в 3-4 шагах напротив первого. Справа и слева от вратаря укладываются маты. Его партнер набрасывает мячи верхом так, чтобы вратарь ловил их в броске, приземляясь на маты.
Периодически занимающиеся меняются ролями. Вратарь встает в ворота, сооруженные из двух набивных мячей. Ширина ворот – 2 шага. Его партнер, заняв позицию в 3 шагах от ворот, набрасывает мяч по крутой траектории в сторону от вратаря. Тот выполняет броски за мячом, пролетая над набивным мячом. Упражнение выполняется в обе стороны. В процессе разучивания приема используются гимнастические маты. Периодически партнеры меняются ролями.
2. Вратарь занимает место в середине ворот. Его партнер с 3-4 шагов верхом набрасывает мячи в сторону от вратаря так, чтобы тот ловил их в броске. Периодически занимающиеся меняются ролями.
3. Упражняются трое игроков. Один из них выполняет роль вратаря. Другой на расстоянии 3 м от первого встает в позицию упор присев на коленях. Третий встает в 3-3,5 шагах от второго. Его задача – набрасывать верхом мячи в сторону от присевшего игрока, чтобы вратарь, сделав несколько шагов, оттолкнувшись в полете через присевшего партнера, выполнял ловлю мяча. После этого упражнение выполняется в другую сторону. В процессе разучивания приема используются гимнастические маты или песок. Пери- одически игроки меняются ролями.
4. Вратарь, заняв позицию в середине ворот, принимает основную стойку. Его партнер встает в 4-5 м против него. Он набрасывает мяч так, чтобы вратарь ловил его в броске после отскока от площадки. Мяч набрасывается то в одну, то в другую сторону от вратаря. Периодически игроки меняются ролями. Вариант: вратарь выполняет упражнение из положения присев или лежа на животе.
5. Вратарь занимает позицию в середине ворот. Партнер встает в 8-10 м от него. По сигналу партнера вратарь делает кувырок вперед и встает в основную стойку. Партнер несильным ударом верхом направляет мяч в сторону от вратаря. Тот в броске пытается овладеть мячом. Постепенно сила удара увеличивается. Периодически партнеры меняются ролями.
6. Игроки поочередно с 10-12 шагов ударом ногой посылают мячи в ворота верхом в сторону от вратаря. Тот ловит высоколетящие мячи в броске.
7. Вратарь занимает позицию в середине ворот. У стоек ворот встают два игрока. Они поочередно набрасывают мячи стоящему в 4-5 шагах от вратаря партнеру, который головой посылает мяч верхом в сторону от вратаря. Последний в броске пытается овладеть высоколетящими мячами. Периодически занимающиеся меняются ролями.
В табл. 1 рассмотрены типичные ошибки, возникающие при освоении техники игры вратаря.
Таблица 1 – Ловля мяча вратарем
| № п/п | Технические ошибки | Их последствия | Как исправить ошибки |
| 1 | При ловле катящегося навстречу вратарю мяча вратарь не успевает подхватить мяч руками | Мяч ударяется в ноги вратарю и отскакивает в поле или в ворота | Выполните из стойки ноги врозь наклоны вперед, не сгибая ноги в коленях, с касанием площадки ладонями |
| 2 | Выйдя на атакующего соперника, вратарь опаздывает с броском на мяч | Соперник направляет мяч в ворота | Вратарь занимает позицию в воротах, а его партнеры поочередно ведут мяч к воротам, преднамеренно отпуская от себя мяч. Вратарь выбегает навстречу и в падении старается овладеть мячом |
| 3 | Мяч, летящий на вратаря ниже груди, отскакивает от него, т.к. он не успел сгруппироваться и образовать туловищем и бедрами «ложе» для мяча | Соперник добивает мяч в ворота | Встав в положение ноги чуть шире плеч, с согнутыми и вытянутыми вперед руками (мяч у него на ладонях), вратарь подтягивает его к груди, обращая внимание на необходимость образования туловищем и бедрами «ложа» длямяча |
| 4 | При ловле высоколетящего мяча он проскакивает между ладоней | Мяч оказывается в воротах | Подбросьте мяч над головой, а затем поймайте, вытягивая руки вверх, ладони обращены к мячу, большие пальцы почти соприкасаются. Выполните 15-18 раз |
Отбивание мячей
В мини-футболе вратарь часто закрыт игроками и видит мяч, летящий в ворота, слишком поздно. Не имея возможности поймать мяч, он вынужден отбивать его руками или ногой.
Отбивание катящихся и низколетящих в стороне от вратаря мячей чаще всего выполняется ногами: в выпаде или шпагате. Отбивание в выпаде (рис 13) является одним из наиболее распространенных приемов. Определив направление движения приближающегося мяча, вратарь делает выпад в эту сторону ближней ногой. При этом его голень ставится почти перпендикулярно (или под небольшим углом) к поверхности площадки, стопа низко выносится над поверхностью площадки и разворачивается перпендикулярно к приближающемуся мячу.
Одновременно в этом же направлении для страховки выносится и одноименная рука. Другая же рука приподнимается, сохраняя равновесие. Мяч принимается на любую часть стопы и голени. В зависимости от ширины выпада туловище вратаря в этот момент принимает или почти вертикальное положение, или наклоняется в сторону выпада. Отбив мяч, вратарь быстро принимает основную стойку. Этим приемом вратарь пользуется для отражения ударов, неожиданно посланных соперниками с разных дистанций.
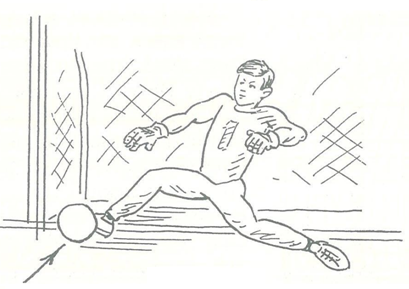
Рисунок 13 – Отбивание катящихся и низколетящих в стороне от вратаря мячей в выпаде
В шпагате отбиваются мячи, летящие в нижние углы ворот (рис.14). Мяч отражается любой частью вытянутой ноги. Отбив мяч, вратарь садится почти в шпагат или же опускается на колено другой ноги. После этого он старается быстро встать и принять основную стойку.
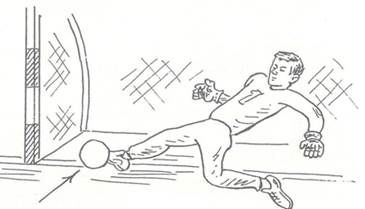
Рисунок 14 – Отбивание катящихся и низколетящих в стороне от вратаря мячей в шпагате
Мячи, летящие в стороне от вратаря, но выше пояса, как правило, отбиваются махом (рис.15). Движение начинается с отведения бедра маховой ноги в сторону приближающегося мяча (голень чуть отстает). Почти одновременно вратарь отталкивается другой ногой в ту же сторону. При этом он должен рассчитать силу толчка так, чтобы принять мяч внутренней стороной стопы или же голенью маховой ноги, которая в этот момент резко приподнимается в сторону вверх. В этот момент туловище вратаря сохраняет вертикальное положение. Для подстраховки одновременно с махом ногой вратарь протягивает в сторону одноименную руку.
Рисунок 15 – Отбивание мячей летящих выше пояса махом
Отбивание мяча ладонью (или ладонями) применяется вратарем в самых разных ситуациях, зачастую непредсказуемых. Так, выходя навстречу атакующему сопернику, вратарь часто не успевает овладеть мячом и в последний момент вынужден отводить его в падении или броске в наиболее безопасное место одной или двумя ладонями (рис.16 а). Эту же технику ему приходится использовать и при отражении мячей, летящих в ворота на разной высоте. Такие мячи отбиваются в сторону от ворот или же переправляются за ворота над перекладиной (рис16 б). Эффективен этот прием и тогда, когда соперник навесным ударом старается перебросить вышедшего вперед стража ворот.
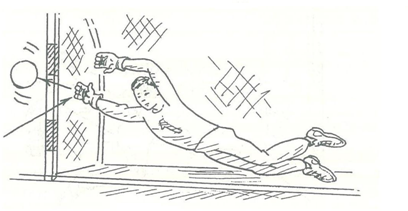
а
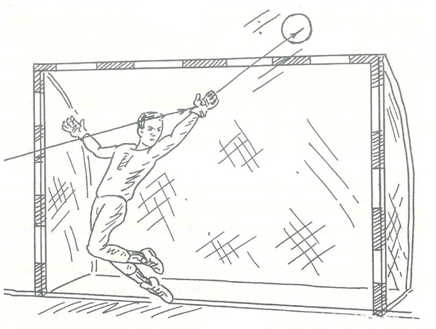
б
Рисунок 16 – Отбивание мяча ладонью
Когда же мяч опускается перед воротами и при этом соперники готовы овладеть им, вратарь отбивает мяч кулаком или кулаками (рис.17). Такой удар выполняется фалангами сжатых в кулак пальцев за счет сгибания рук в локтевых суставах.
Удар выполняется, как правило, в прыжке. Используется этот прием и при попытках соперника перебросить навесным ударом вышедшего вперед вратаря».
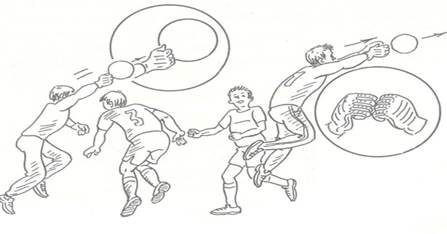
Рисунок 17 – Отбивание мяча кулаком
Если мяч оказался в воздухе прямо над вратарем или перед ним тогда, когда он ждал его в другой точке или вообще не предвидел такой ситуации и потому оказался неподготовленным к ловле или отбиванию руками, а соперники готовы добить мяч в ворота, – страж ворот должен мгновенно сориентироваться и ликвидировать возникшую у ворот опасность, отбив этот мяч головой (рис.18).
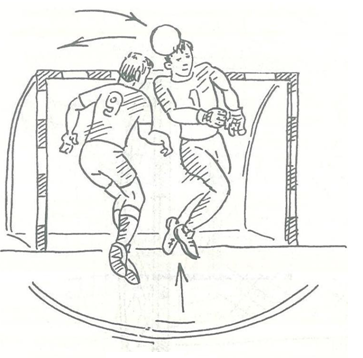
Рисунок 18 – Отбивание мяча головой
1. Вратарь занимает позицию в середине ворот, спиной к центру площадки. Его партнер встает между 6-метровой отметкой и линией ворот. Он подает вратарю звуковой сигнал. Вратарь быстро разворачивается на 180° и принимает основную стойку. Его партнер ударом ногой направляет мяч низом в сторону от вратаря так, чтобы тот отбивал его в выпаде. Мячи направляются то в одну, то в другую сторону от вратаря. Вариант: а) то же, но мяч отбивается в шпагате; б) партнер набрасывает мячи руками на уровне пояса вратаря, а тот отбивает их махом ноги.
2. Вратарь занимает позицию на 6-метровой отметке, лицом к центру площадки. В 3-х м позади него встает партнер. Он направляет ударом ногой мячи низом то в одну, то в другую сторону от вратаря, подав предварительно звуковой сигнал. Сконцентрировав внимание, вратарь в падении отбивает мячи рукой, как только они появятся в поле его зрения. Необходимо, чтобы вратарь отбивал мячи в момент, когда они еще не пересекли линию штрафной площади. Периодически партнеры меняются ролями.
3. Вратарь занимает позицию в середине ворот в положении сидя, лицом к центру площадки. Его партнер, встав в 3-4 м напротив, поочередно бросает мячи так, чтобы, отскочив от поверхности площадки, они проходили в ворота рядом с вратарем. Тот, не вставая, тянется за отскочившими мячами, стараясь отбить их ладонями в сторону от ворот. Периодически партнеры меняются ролями с вратарем.
4. Занимающиеся с мячами встают в колонну по одному в 12-15 шагах от ворот. Вратарь занимает позицию в середине ворот. Игроки поочередно ведут мяч в сторону ворот. Войдя в штрафную площадь, они умышленно несколько отпускают мяч от себя. Вратарь, выбежав навстречу атакующему игроку, в броске ладонью отбивает мяч в сторону и т.д. Вариант: то же, но игроки ведут мяч в сторону ворот то с одного, то с другого фланга.
Типичные ошибки, возникающие у начинающего вратаря при отбивании мячей, рассмотрены в табл. 2.
Таблица 2 -Отбивание мячей
| № п/п | Технические ошибки | Их последствия | Как исправить ошибки |
| 1 | Стремясь отбить низколетящий мяч в выпаде или шпагате, вратарь не успел отбить мяч ногой | Гол | Выполняйте из основной стойки вратаря выпады то в одну сторону, то в другую сторону. Затем попросите товарища направлять ударом ногой низом в ворота и отбивайте их в выпаде или шпагате |
| 2 | Вратарь не успел перевести ладонью над перекладиной мяч, летящий в ворота по крутой траектории | Гол | Попросите друзей навешивать мячи на ворота. Выполняйте отбивание летящих мячей, переводя их ладонью над Перекладиной |
| 3 | Выбежав навстречу атакующему сопернику, вратарь не успел в броске ладонью отбить мяч | Опасный момент у ворот | Повторите упражнение 8 |
Вбрасывание мяча
В мини-футболе вратарь выполняет вбрасывание мяча после выхода мяча за линию ворот, а также после ловли его в пределах штрафной площади. Задача стража ворот – точно и быстро направить мяч рукой свободному партнеру. Вбрасывание, как правило, осуществляется одной рукой из-за плеча, сбоку или снизу (рис.19).
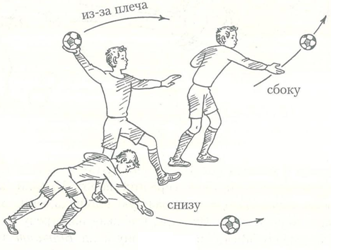
Рисунок 19 – вбрасывание мяча
При вбрасывании из-за плеча рука вратаря, поддерживающая мяч, сгибается в локте и поднимается до уровня головы. Вес его тела переносится на сзади стоящую ногу. Свободная рука, согнутая в локте, находится перед грудью. Бросок начинается движением предплечья вперед-вниз и заканчивается энергичным движением кисти. В результате мяч летит в направлении избранной вратарем цели. В тот же момент свободная рука вытягивается в сторону, а вес тела перемещается на впереди стоящую ногу. Затем вратарь переступает вперед ногой, которая до броска находилась сзади.
Тренировочные упражнения
1. Занимающиеся встают в колонну по одному. В 4-6 шагах напротив располагается партнер с мячом. Он «выкатывает» мяч рукой головному игроку. Тот, подобрав мяч, такимжеобразомнаправляетегообратно,асамперебегаетвконецколонны.Теперьмяч
«выкатывается» второму номеру и т.д. Периодически занимающиеся меняются ролью со стоящим напротив колонны партнером.
2. Занимающиеся упражняются в парах. Расстояние между партнерами -6-7 шагов. Игроки поочередно «выкатывают» мяч друг другу, предварительно выполняя ловлю мяча условленным способом.
3. Занимающиеся упражняются в парах. Расстояние между партнерами 8-10 шагов. Они поочередно направляют мяч друг другу броском из-за плеча с места. Вариант: то же, но броски выполняются одной рукой сбоку с места.
4. Стоя в 4-5 м от стенки, вратарь различными способами направляет мяч рукой в это препятствие, акцентируя внимание на энергичном заключительном движении кистируки.
5. На площадке на расстоянии 20, 25 и 35 шагов от ворот обозначьте три круга диаметром 1-1,5 м. Поупражняйтесь в попадании в ту или иную цель броском различными способами с места.
6. Вратари упражняются в парах. Партнеры встают в 20-30 шагах друг против друга и поочередно ударом ногой с лёта или с полулёта посылают мячи верхом, предварительно подбросив мяч перед собой.
7. В 30-35 шагах от штрафной площади обозначаются два круга диаметром 1,5-2 метра. Расстояние между кругами 5-6 м. Вратарь занимает место в воротах. Его партнер набрасывает мяч на вратаря верхом. Поймав мяч, вратарь подбрасывает мяч перед собой и направляет его в указанную партнером цель ударом с лёта или с полулёта. Вариант: партнер «накатывает» мяч на вратаря низом.
В табл. 3 рассмотрены ошибки, часто возникающие при освоении приёма вбрасывания мяча.
Таблица 3 -Вбрасывание мячей
| № п/п | Технические ошибки | Их последствия | Как исправить ошибки |
| 1 | Выполняя «выкатывание» мяча партнеру, вратарь не продолжил движения рукой за катящимся мячом | Соперник перехватил медленно катящийся мяч | Повторите упражнения 1, 2 |
| 2 | Выполняя вбрасывание мяча рукой сбоку, вратарь не сделал широкий размах рукой с мячом | Мяч не долетел до адресата | Повторите упражнения 3, 4 |
| 3 | Выполняя вбрасывание мяча одной рукой от плеча, вратарь не сделал завершающегося движения кистью | Мяч не дошел до партнера | Повторите упражнения 3, 4 |
Дополнительные упражнения для вратарей
В мини-футболе страж ворот должен в полной мере владеть не только специфической техникой ловли, отбивания и введения мяча в игру, но и техникой полевых игроков. Такая необходимость диктуется самой сутью мини-футбола, в котором вратарю то и дело приходится выполнять функции полевых игроков. Например, получив мяч в ноги от партнера, вратарь должен точно послать мяч одному из игроков своей команды так, чтобы соперники не перехватили передачу. Кроме того, складывающиеся на площадке ситуации требуют от вратаря надежно выполнять прием мяча разными способами, использовать разнообразные обманные движения, а также, подключаясь к атаке, наносить сильный и точный удар по воротам соперников ит.д.
Хорошая техническая оснащенность требуется вратарю, когда, оставаясь последним игроком обороны, он вынужден выполнять функции страхующего или диспетчера. Естественно, чтобы в полной мере отвечать таким требованиям, страж ворот должен на тренировочных занятиях не только отрабатывать специфические приемы игры вратаря, но и участвовать в упражнениях полевых игроков, а также в качестве полевого игрока иной раз и принимать участие в играх. И все же основной заботой вратаря является, безусловно, освоение им специфической техники игроков этого амплуа. Те, из вас кто уже определился со своей игровой специальностью и освоил азы игры вратаря, могут перейти к выполнению дополнительных упражнений. Ряд из них вы сможете выполнять индивидуально, а другие с группой своих друзей-партнеров по тренировочным занятиям.
1. Занимающиеся держат мяч в одной руке, выполняя этой рукой круговые движения вперед и назад. Упражнение выполняется попеременно правой и левой рукой.
2. Вратарь вытягивает руки в стороны – вверх, перебрасывая мяч с руки на руку.
3. Вратарь держит мяч в руках. Наклоняясь вперед, он бросает мяч между ног за спину так, чтобы он пролетел над головой. Выпрямившись, вратарь ловит мяч перед собой. Вариант: после броска мяч направляется вверх. Выпрямившись, вратарь разворачивается на 180° и ловит мяч над головой.
4. Наклонившись вперед, вратарь перекладывает мяч из руки в руку вокруг туловища или ног. Вариант: а) мяч перекладывается из руки в руку по «восьмерке»; б) мяч перекатывается по поверхности площадки вокруг ног или по«восьмерке».
5. Вратарь садится, приподняв выпрямленную ногу, и перекладывает мяч из руки в руку так, чтобы мяч проходил под этой ногой.
6. Вратарь стоит, держа мяч в вытянутых вперед руках. Отпустив мяч, он ловит его перед самым падением на площадку и прижимает к груди. Вариант: то же, но вратарь ловит мяч после отскока от площадки.
7. Вратарь стоит, держа мяч в вытянутой в сторону правой руке. Ударяя мячом о поверхность площадки у себя под ногами, он подскакивает, а затем перехватывает отскочивший от площадки мяч обеими руками. Затем мяч перекладывается в левую руку и таким же образом броском направляется вратарем себе под ноги ит.д.
8. Вратарь подбрасывает мяч высоко над собой обеими руками. Поймав мяч в прыжке в наивысшей точке, он прижимает его к груди. Вариант: то же, но после броска вратарь быстро поворачивается на 360°, стараясь поймать мяч и прижать его к груди.
9. Вратарь принимает исходное положение, лежа на спине с мячом в вытянутых руках. Быстро поднявшись, он переводит мяч на грудь. Вариант: упражнение выполняется из исходных положений лежа на боку и лежа на животе.
10. Вратарь принимает исходное положение, лежа в упоре на руках. Его партнер набрасывает ему мяч на уровне головы. Вратарь старается поймать летящий мяч, приземляясь на грудь. Вариант: вратарь принимает положение, сидя на коленях, а партнер набрасывает ему мяч на высоту вытянутых рук или несколько в сторону.
11. Вратарь принимает основную стойку, повернувшись спиной к партнеру. Тот стоит в 5 м от вратаря с мячом в руках. По звуковому сигналу он бросает мяч в сторону вратаря. Тот быстро разворачивается на 180° и ловит мяч и т.д.. Вариант: мяч набрасывается несколько в сторону от вратаря или на уровне его вытянутых рук.
12. Справа и слева от вратаря (в 1,5-2 шагах от него) кладется по набивному мячу. Вратарь, приняв основную стойку, бросает мяч вправо так, чтобы тот катился мимо набивного мяча, и в броске старается поймать катящийся мяч. Затем упражнение выполняется в другую сторону ит.д.
13. Вратарь держит мяч над головой. Сильно бросив мяч в площадку перед собой, он выполняет кувырок вперед и, прежде чем мяч вторично коснется площадки, ловит его и прижимает к груди. Вариант: после броска вратарь поворачивается на 180°, выполняет кувырок назад и ловит мяч.
14. Вратарь занимает позицию лицом к стенке на расстоянии 1,5-2 шага. Его партнер встает позади вратаря и бросает мяч в стенку. Задача вратаря -среагировав на звук отскочившего от стенки мяча, овладеть им. Постепенно сила броска увеличивается. Периодически партнеры меняются ролями. Вариант: а) партнер занимает позицию сзади- сбоку от вратаря. Последний стоит лицом к стенке на расстоянии 5 м. Мяч набрасывается в стенку по крутой траектории. Вратарь выбегает вперед и в прыжке ловит мяч в наивысшей точке; б) мячи направляются в стенку на разной высоте.
15. Два вратаря встают в 10-12 м друг против друга. Один из них с мячом совершает кувырок вперед, встает и ногой направляет мяч в сторону партнера по крутой траектории. Последний ловит мяч в прыжке и прижимает его к груди. Выполнив кувырок, он также посылает мяч верхом партнеру ит.д.
Комплексные числа. реферат. математика. 2021-10-12
Введение
Рассмотрев тему «комплексные числа» на занятиях
высшей математики мы заинтересовались данной темой и решили углубить свои
познания в этой области.
Большое значение комплексных чисел в математике
и её приложениях широко известно. Их изучение имеет самостоятельный интерес.
Алгебру комплексных чисел можно успешно использовать в элементарной геометрии,
тригонометрии, теории геометрических преобразований, а также в электротехнике и
различных задачах с механическим и физическим содержанием.
История комплексных чисел
Древнегреческие математики считали
“настоящими” только натуральные числа. Постепенно складывалось
представление о бесконечности множества натуральных чисел.
В III
веке Архимед разработал систему обозначения вплоть до такого громадного как
Наряду с натуральными числами применяли дроби –
числа, составленные из целого числа долей единицы. В практических расчетах
дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем
Вавилоне. Долгое время полагали, что результат измерения всегда выражается или
в виде натурального числа, или в виде отношения таких чисел, то есть дроби.
Древнегреческий философ и математик Пифагор учил, что “… элементы чисел
являются элементами всех вещей и весь мир в челом является гармонией и числом.
Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из
пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной.
Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить
длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с
этого открытия начинается эра теоретической математики: открыть существование
несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению,
было невозможно.
Следующим важным этапом в развитии понятия о
числе было введение отрицательных чисел – это было сделано китайскими
математиками за два века до н. э. Отрицательные числа применяли в III
веке древнегреческий математик Диофант, знавший уже правила действия над ними,
а в VII веке эти
числа уже подробно изучили индийские ученые, которые сравнивали такие числа с
долгом. С помощью отрицательных чисел можно было единым образом описывать
изменения величин. Уже в VIII
веке было установлено, что квадратный корень из положительного числа имеет два
значения – положительное и отрицательное, а из отрицательных чисел квадратный
корень извлекать нельзя: нет такого числа 
,
чтобы 
.
В XVI
веке в связи с изучением кубических уравнений оказалось необходимым извлекать
квадратные корни из отрицательных чисел. В формуле для решения кубических
уравнений вида 
кубические и
квадратные корни
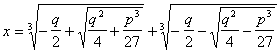
Эта формула безотказно действует в случае, когда
уравнение имеет один действительный корень (
),
а если оно имеет три действительных корня (
),
то под знаком квадратного корня оказывалось отрицательное число. Получалось,
что путь к этим корням ведет через невозможную операцию извлечения квадратного
корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й
степени, математики усиленно искали формулу для решения уравнения 5-й степени.
Но Руффини (Италия) на рубеже XVIII
и XIX веков доказал, что
буквенное уравнение пятой степени 
нельзя
решить алгебраически; точнее: нельзя выразить его корень через буквенные
величины a, b,
c, d,
e с помощью шести
алгебраических действий (сложение, вычитание, умножение, деление, возведение в
степень, извлечение корня).
В 1830 году Галуа (Франция) доказал, что никакое
общее уравнение, степень которого больше чем 4, нельзя решить алгебраически.
Тем не менее всякое уравнение n-й степени имеет (если рассматривать и
комплексные числа) n корней
(среди которых могут быть и равные). В этом математики были убеждены еще в XVII
веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже
XVIII и XIX
веков
упомянутая теорема была доказана Гауссом.
Итальянский алгебраист Дж. Кардано в 1545 г.
предложил ввести числа новой природы. Он показал, что система уравнений 
,
не имеющая решений во множестве действительных чисел, имеет решения вида 
,
,
нужно только условиться действовать над такими выражениями по правилам обычной
алгебры и считать что 
. Кардано называл
такие величины “чисто отрицательными” и даже “софистически
отрицательными”, считал их бесполезными и старался их не употреблять. В
самом деле, с помощью таких чисел нельзя выразить ни результат измерения
какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году
вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены
первые правила арифметических операций над такими числами, вплоть до извлечения
из них кубических корней. Название “мнимые числа” ввел в 1637 году французский
математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII
века – Л. Эйлер предложил использовать первую букву французского слова imaginaire
(мнимый) для обозначения числа 
(мнимой единицы).
Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин
“комплексные числа” так же был введен Гауссом в 1831 году. Слово
комплекс (от латинского complexus)
означает связь, сочетание, совокупность понятий, предметов, явлений и т. д.
Образующих единое целое.
В течение XVII
века продолжалось обсуждение арифметической природы мнимых чисел, возможности
дать им геометрическое обоснование.
Постепенно развивалась техника операций над
мнимыми числами. На рубеже XVII
и XVIII веков была
построена общая теория корней n-ых
степеней сначала из отрицательных, а за тем из любых комплексных чисел,
основанная на следующей формуле английского математика А. Муавра (1707)
С помощью этой формулы можно было так же вывести
формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году
замечательную формулу : 
, которая связывала
воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера
можно было возводить число e
в любую комплексную степень. Любопытно, например, что 
.
Можно находить sin
и cos от комплексных
чисел, вычислять логарифмы таких чисел, то есть строить теорию функций
комплексного переменного.
В конце XVIII
века французский математик Ж. Лагранж смог сказать, что математический анализ
уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать
решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие
уравнения встречаются, например, в теории колебаний материальной точки в
сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял
комплексные числа для решения интегралов.
Хотя в течение XVIII
века с помощью комплексных чисел были решены многие вопросы, в том числе и
прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще
не было строго логического обоснования теории этих чисел. По этому французский
ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, –
только наведение, приобретающее характер настоящих истин лишь после
подтверждения прямыми доказательствами.
“Никто ведь не сомневается в точности
результатов, получаемых при вычислениях с мнимыми количествами, хотя они
представляют собой только алгебраические формы иероглифы нелепых
количеств” Л. Карно.
В конце XVIII
века, в начале XIX
века было получено геометрическое истолкование комплексных чисел. Датчанин К.
Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили
изобразить комплексное число 
точкой 
на
координатной плоскости. Позднее оказалось, что еще удобнее изображать число не
самой точкой M, а вектором 
,
идущим в эту точку из начала координат.
При таком истолковании сложение и вычитание
комплексных чисел соответствуют эти же операции над векторами. Вектор можно
задавать не только его координатами a
и b, но так же длиной r
и углом j, который он
образует с положительным направлением оси абсцисс.
При этом 
,
и
число z принимает вид 
,
который называется тригонометрической формой комплексного числа. Число r
называют модулем комплексного числа z
и обозначают 
. Число 
называют
аргументом z и обозначают ArgZ.
Заметим, что если 
, значение ArgZ
не определено, а при 
оно определено с
точностью до кратного 
.
Упомянутая ранее формула Эйлера позволяет
записать число z в виде 
(показательная
форма комплексного числа).
Геометрическое истолкование комплексных чисел
позволило определить многие понятия, связанные с функцией комплексного
переменного, расширило область их применения.
Стало ясно, что комплексные числа полезны во
многих вопросах, где имеют дело с величинами, которые изображаются векторами на
плоскости: при изучении течения жидкости, задач теории упругости.
После создания теории комплексных чисел возник
вопрос о существовании “гиперкомплексных” чисел – чисел с несколькими
“мнимыми” единицами.
Такую систему вида
где 
,
построил в 1843 году ирландский математик У. Гамильтон, который назвал их
“кватернионами”.
Правила действия над кватернионами напоминает
правила обычной алгебры, однако их умножение не обладает свойством
коммутативности (переместительности): например, 
,
а 
.
Гиперкомплексные числа не являются темой этого реферата, поэтому лишь упомянем
об их существовании.
Большой вклад в развитие теории функций комплексного
переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее
применениями к упругости, М. В. Келдыш и М. А. Лаврентьев – к аэро- и
гидродинамике, Н. Н. Богомолов и В. С. Владимиров – к проблемам квантовой
теории поля.
Комплексное число имеет вид a
bi; здесь a
и b – действительные
числа , а i – число нового
рода, называемое мнимой единицей.
“Мнимые” числа составляют частный вид
комплексных чисел (когда а = 0). С другой стороны, и действительные числа
являются частным видом комплексных чисел (когда b
= 0).
Действительное число a
назовем абсциссой комплексного числа a
bi; действительное
число b – ординатой
комплексного числа a bi.
Основное свойство числа i
состоит в том, что произведение i*i
равно -1, т.е.
i2= -1
Долгое время не удавалось найти такие физические
величины, над которыми можно выполнять действия, подчинённые тем же правилам,
что и действия над комплексными числами – в частности правилу (1). Отсюда
названия: “мнимая единица”, “мнимое число” и т.п. В настоящее время известен
целый ряд таких физических величин, и комплексные числа широко применяются не
только в математике, но также и в физике и технике.
Оставим в стороне вопрос о геометрическом или
физическом смысле числа i,
потому что в разных областях науки этот смысл различен.
Правило каждого действия над комплексными
числами выводится из определения этого действия. Но определения действий над
комплексными числами не вымышлены произвольно, а установлены с таким расчетом,
чтобы согласовались с правилами действий над вещественными числами. Ведь
комплексные числа должны рассматриваться не в отрыве от действительных, а
совместно с ними.
отрезок комплексный число
Соглашение о комплексных числах
1. Действительное
число а записывается также в виде a
0i (или a
– 0i).
Примеры. Запись 3 0i
обозначает то же, что запись 3. Запись -2 0i
означает -2.
2. Комплексное
число вида 0 bi
называется “чисто мнимым”. Запись bi
обозначает то же, что 0 bi.
3. Два
комплекных a bi,
a’ b’i
считаются равными, если у них соответственно равны абсциссы и ординаты, т. е.
Если a = a’,
b = b’.
4. В
противном случае комплексные числа не равны. Это определение подсказывается
следующим соображением. Если бы могло существовать, скажем, такое равенство: 2
5i = 8 2i,
то по правилам алгебры мы имели бы i
= 2, тогда как i не должно
быть действительным числом.
Замечание. Мы еще не определили, что такое
сложение комплексных чисел. Поэтому, строго говоря, мы ещё не в праве
утверждать, что число 2 5i
есть сумма чисел 2 и 5i.
Точнее было бы сказать, что у нас есть пара действительных чисел: 2 (абсцисса)
и 5 (ордината); эти числа порождают число нового рода, условно обозначаемое 5
7i.
Сложение комплексных чисел
Определение. Суммой комплексных чисел a
bi и a’
b’i
называют комплексное число (a
a’) (b
b’)i.
Это определение подсказывается правилами
действий с обычными многочленами.
Пример 1. (-3 5i) (4 – 8i) = 1 –
3i
Пример 2. (2 0i) (7 0i) = 9
0i. Так
как запись 2 0i означает то
же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой
(2 7=9).
Пример 3. (0 2i) (0 5i) = 0
7i, т. е. 2i 5i = 7i
Пример 4. (-2 3i)
( – 2 – 3i) = – 4
В примере 4 сумма двух комплексных чисел равна
действительному числу. Два комплексных числа a bi
и a-bi
называются сопряженными. Сумма сопряженных комплексных чисел равна
действительному числу.
Замечание. Теперь, когда действие сложения
определено, мы имеем право рассматривать комплексное число a
bi как сумму чисел a
и bi. Так, число 2 и
число 5i в сумме дают число
2 5i.
Вычитание комплексных чисел.
Оп ределение.
Разностью комплексных чисел a
bi (уменьшаемое) и a’
b’i
(вычитаемое) называется комплексное число (a
– a’) (b
– b’)i.
Пример 1. (-5 2i) – (3 – 5i) = -8
7i
Пример 2. (3 2i) – (-3 2i) = 6
0i = 6
Умножение комплексных чисел.
Определение умножения комплексных чисел
устанавливается с таким расчетом, чтобы 1) числа a
bi и a’
b’i
можно было перемножать, как алгебраические двучлены, и чтобы 2) число i
обладало свойством i 2= – 1. В
силу требования 1) произведение (a
bi)(a’
b’i)
должно равняться aa’
(ab’ ba’)i
bb’i2
, а в силу требования 2) это выражение должно равняться (aa’
– bb’) (ab’
ba’)i.
В соответствии с этим устанавливается следующее определение.
Определение. Произведением комплексных чисел a
bi и a’
b’i
называется комплексное число (aa’
– bb’) (ab’
ba’)i.
Замечание 1. Равенство i2
= -1 до установленного правила умножения комплексных чисел носило характер
требования. Теперь оно вытекает из определения. Ведь запись i
2 , т. е. i*i,
равнозначна записи (0 1*i)(0
1*i). Здесь a
= 0, b = 1, a’
= 0, b’ = 1 Имеем aa’
– bb’ = -1, ab’
ba’ = 0, так что
произведение есть -1 0i,
т. е. -1.
Замечание 2. На практике нет нужды пользоваться
формулой произведения. Можно перемножить данные числа, как двучлены, а затем
положить, что i2 = -1.
Пример 1. (1 – 2i)(3 2i) = 3 – 6i
2i – 4i 2 = 3 – 6i 2i 4 = 7 – 4i.
Пример 2. (a bi)(a – bi) = a2 b
2
Пример 2 показывает, что произведение
сопряженных комплексных чисел есть действительное и притом положительное число.
В соответсвии с определением деления
действительных чисел устанавливается следующее определение.
Опредление. Разделить комплексное число a
bi на комплексное
число a’ b’i
– значит найти такое число x
yi, которое, будучи
помножено на делитель, даст делимое.
Если делитель не равен нулю, то деление всегда
возможно, и частное единственно (доказательство смотри в замечании 2). На
практике частное удобнее всего находить следующим образом.
Пример 1. Найти частное (7 – 4i):(3
2i).
Записав дробь (7 – 4i)/(3
2i), расширяем её на
число 3 – 2i, сопряженное с 3
2i. Получим:
((7 – 4i)(3 – 2i))/((3 2i)(3 –
2i)) = (13 – 26i)/13 = 1 – 2i.
Пример 2. (-2 5i)/(-3 -4i) = ((-2
5i)(-3 – 4i))/((-3 – 4i)( -3 4i)) = (-14 -23i)/25 = -0,56 – 0.92i.
Чтобы доказать, что правая часть действительно
является частным, достаточно помножить её на a’
b’. Получим a
bi.
Геометрический смысл сложения и вычитания
комплексных чисел
Пусть векторы ОМ и ОМ’ (рис. 1) изображают
комплексные числа z= x
yi u
z’ = x’
y’i.
Из точки М проведем вектор МК, равный OM’.
Тогда вектор ОК изображает сумму данных комплексных чисел.
Построенный указанным образом вектор ОК
называется геометрической суммой векторов ОМ и ОМ’.
Итак, сумма двух комплексных чисел
представляется суммой векторов, изображающих отдельные слагаемые.
Длина стороны ОК треугольника ОМК меньше суммы и
больше разницы длин ОМ и МК. Поэтому
||z|
– |z’|| < |z
z’| < |z|
|z’|.
Рис. 1
Равенство имеет смысл только в тех случаях,
когда векторы ОМ и ОМ’ имеют одинаковые или противоположные направления. В
первом случае |OM|
|OM’| = |OK|,
т. е. |z z’|=|z|
|z’|. Во втором
случае |z z’|=||z|
– |z’||.
Геометрическая интерпретация комплексных чисел.
Длина отрезка
При заданной прямоугольной декартовой системе
координат на плоскости комплексному числу z = x iy (i2= -1) можно взаимно
однозначно поставить в соответствие точку М плоскости с координатами х, у (рис.1)
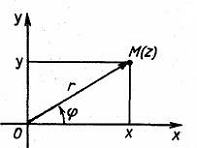
Рис. 2
.
Число z тогда называют комплексной
координатой точки М.
Поскольку множество точек евклидовой
плоскости находится во взаимно однозначном соответствии с рис. 2 множеством
комплексных чисел, то эту плоскость называют
также плоскостью комплексных чисел.
Начало О декартовой системы координат называют при этом начальной или нулевой
точкой плоскости комплексных чисел.
При у=0 число z
действительное. Действительные числа изображаются точками оси х, поэтому она
называется действительной осью. При х=0 число z чисто
мнимое: z=iy. Мнимые
числа изображаются точками оси у, поэтому она называется мнимой осью. Нуль – одновременно
действительное и чисто мнимое число.
Paccтoяниe от начала О
плоскости до точки М(z) называется модулем комплексного числа z и
обозначается |z| или r
|z| = r = |OM| = 
.
Если 
– ориентированный угол,
образованный вектором 
с осью х, то
по определению функции синуса и косинуса
откуда 
и поэтому 
.
Такое представление комплексного
числа z называется его тригонометрической формой. Исходное представление z=x iy называют
алгебраической формой этого числа. При тригонометрическом представлении угол называют
аргументом комплексного числа и обозначают еще через arg z:
.
Если дано комплексное число z=x iy, то число 
называется
комплексно-сопряженным (или просто сопряженным) этому числу z. Тогда, очевидно,
и число z сопряжено числу 
. Точки М(z)
и 
симметричны
относительно оси х (рис.2).
Из равенства 
следует y=0 и
обратно. Это значит, что число, равное своему сопряженному, является
действительным и обратно.
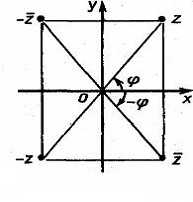
Рис. 3
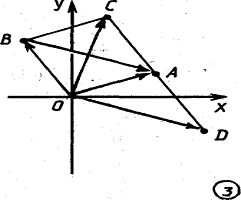
Рис. 4
Точки с комплексными координатами z и -z
симметричны относительно начальной точки О (рис.3). Точки с комплексными
координатами z и 
симметричны
относительно оси у. Из равенства z= вытекает x=0 и
обратно. Поэтому условие z= является критерием чисто мнимого
числа. Для любого числа z, очевидно, |z| = || = |-z| = ||.
Сумма и произведение двух
сопряженных комплексных чисел являются действительными числами
Число, сопряженное с суммой,
произведением или же частным комплексных чисел, есть соответственно сумма,
произведение или же частное чисел, сопряженных данным комплексным числам:
Эти равенства можно легко проверить,
пользуясь формулами для операций над комплексными числами. Каждой точке М(z)
плоскости – взаимно однозначно соответствует вектор . Поэтому
комплексные числа можно интерпретировать векторами, приложенными к точке O.
Сложению и вычитанию комплексных чисел отвечает сложение и вычитание
соответствующих им векторов. Именно если а и b – комплексные координаты точек A
и В соответственно, то число с=а b является координатой точки С, такой, что 
(рис.4).
Комплексному числу d=a-b соответствует такая точка D, что 
.
Расстояние между точками А и В равно
:
|АВ| = |а-b|
Так как |z|2= z, то
|AB|2=(a-b)(
)
Уравнение z= r2 определяет
окружность с центром О радиуса r. Отношение 
, в котором
точка С делит данный отрезок АВ, выражается через комплексные координаты этих
точек так:
откуда 
Если положить 
и 
, то
Условия (4) необходимы и достаточны
для того, чтобы точки А, В, С были коллинеарны. При 
точка С
является серединой отрезка AB, и обратно. Тогда:
c = 
Пусть имеем параллелограмм ABCD. Его центр
имеет комплексную координату 
= 
при условии, что точки А, В, С, D имеют
соответственно комплексные координаты а, b, с, d. Если не
исключать случай вырождения параллелограмма, когда все его вершины оказываются
на одной прямой, то равенство a c = b d (5)
является необходимым и достаточным условием того, чтобы четырехугольник ABCD
был параллелограммом.
C
B B
C
N
M MЬ
A
D A D
Рис.
5 Рис. 6
Задача 1. Точки М и N – середины диагоналей АС и
BD четырехугольника
ABCD. (Рис.5)
Доказать, что |AB|2 |BC|2 |CD|2 |DA|2 = |AC|2 |BD|2 4|MN|2.
Решение. Пусть точкам A,
В, С, D, М, N соответствуют комплексные числа а, b,
с, d, т, п.
Так как m = и n = , то
|AB|2 |BC|2 |CD|2 |DA|2 
|AC|2 |BD|2 4|MN|2 
Равенство доказано.
Задача 2. Доказать, что если в плоскости
параллелограмма ABCD существует такая точка М, что |MA|2 |MC|2=|MB|2 |MD|2, тo ABCD
– прямоугольник. (Рис.6)
Решение. Если за начальную точку
принять центр параллелограмма ABCD, то при принятых ранее обозначениях с= -a, d= -b, и поэтому
данное в условии равенство будет эквивалентно равенству 
, которое
означает, что диагонали параллелограмма равны, т. е. он прямоугольник.
Уравнение высших степеней, уравнение
деления круга на пять частей
В основе решения уравнений выше второй степени
лежит теорема о рациональных корнях многочлена
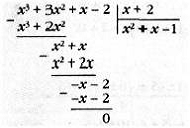
Если несократимая дробь p/q является
корнем многочлена P(x)=
с целыми
коэффициентами, то её числитель p является делителем свободного
члена, а знаменатель q – делителем старшего коэффициента .
Для доказательства достаточно
подставить в ур-е P(x)=0 x=p/q и умножить
ур-е на 
. Получим
Все слагаемые в левой части, кроме
последнего, делятся на р, поэтому и 
делится на р, а поскольку q и р –
взаимно простые числа, р явл-ся делителем 
. Доказательство для q аналогично.
С помощью этой теоремы можно найти
все рациональные корни ур-я с целыми коэфф-ми испытанием конечного числа
«кандидатов». Например, для ур-я 
, старший коэфф-т которого равен 1,
«кандидатами» будут делители числа -2. Их всего четыре: 1, -1, 2, -2. Проверка
покажет, что корнем явл-ся только одно из этих чисел: 
.
Если один корень найден, можно
понизить степень ур-я. Согласно теореме Безу, остаток от деления многочлена P(x) на двучлен
х-с равен P(c), т.е.
Р(х)=(х-с)Q(х) Р(с).
Из теоремы непосредственно следует,
что
Если с – корень многослена Р(х), то
многочлен делится на х-с, т.е. Р(х)=(х-с)Q(х), где Q(x) –
многочлен степени, на 1 меньшей, чем Р(х).
Продолжая наш пример, вынесем из
многочлена 
множитель 
. Чтобы
найти частное Q(x), можно
выполнить деление «уголком», как показано на рис. 7. Но есть и более простой
способ. Он станет понятен из примера:
Теперь остаётся решить квадратное
уравнение х2 х-1=0. Его корни:
Если у многочлена с целыми
коэффициентами рациональных корней не оказалось, можно попробовать разложить
его на множители меньшей степени с целыми коэффициентами. Рассмотрим, например,
уравнение:
Представим левую часть в виде
произведения двух квадратных трёхчленов с неизвестными (неопределёнными)
коэффициентами:
Раскроем скобки в правой части и
приведём подобные:
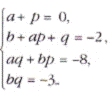
Теперь, приравнивая коэффициенты при
одинаковых степенях х в обеих частях, получим систему уравнений 
Попытка решить эту систему в общем
виде вернула бы нас назад, к решению исходного уравнения. Но целые корпи, если
они существуют, нетрудно найти и подбором. Не ограничивая общности, можно
считать, что 
, тогда
последнее уравнение показывает, что надо рассмотреть лишь два варианта: b = 3, q=-1 и b=1, q=-3.
Подставляя эти пары значений в остальные уравнения, убеждаемся, что первая из
них даёт искомое разложение:
Этот способ решения уравнений
называется методом неопределённых коэффициентов.
Если уравнение имеет вид P(Q(x)) = 0, где
Р и Q –
многочлены, то замена у = Q(x) сводит его
решение к решению двух уравнений меньших степеней: Р(у) = 0 и Q(x) = у.
Замена используется, в частности, при решении биквадратных уравнений.
Более интересный случай – возвратные
уравнения, т. е. уравнения чётной степени
,
в которых коэффициенты, одинаково
отстоящие от концов, равны: 
= 
, 
= 
и т. д. Такое уравнение сводится к
уравнению вдвое меньшей степени делением на 
и последующей заменой у = х± 1/x.
Рассмотрим, например, уравнение
.
Поделив его на х2 (что законно, так
как х = 0 не является корнем), получаем
.
Заметим, что
.
Поэтому величина у = х 1/х
удовлетворяет квадратному уравнению у ау b
– 2 = 0, решив которое можно найти х из уравнения х2-ух 1 =0.
При решении возвратных уравнений
более высоких степеней обычно используют тот факт, что выражение 
при любом k можно
представить как многочлен степени k от у = х
1/х.
Описанные здесь приёмы используются
при исследовании (в комплексных числах) уравнения деления круга на пять частей:
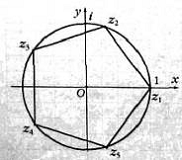
Рис. 7
Уравнение называется так потому, что
если его корпи отметить па комплексной плоскости, то они попадут в вершины
правильного пятиугольника, вписанного в единичную окружность, причём одной из
вершин будет точка с координатами (1;0) (рис.8). Используя тригонометрическое
представление комплексного числа, эти корни можно записать следующим образом:
, k=1, 2, 3, 4,
5.
Среди них находится и единственный
действительный корень ь
.
Спрашивается, можно ли выразить остальные.
Попробуем сделать это.
Поскольку один корень, х=1, нам известен, понизим степень уравнения, вынося из
его левой части двучлен х-1:
Остаётся
уравнение
Оно возвратное, делим его на 
:
.
Подставляем z=x 1/x:
Корни этого квадратно уравнения
.
Для х получаем уравнение 
, или
Отсюда
.
Таким образом, наше уравнение
допускает решение в радикалах, и даже в квадратных радикалах. Последнее
означает что правильный пятиугольник можно построить с помощью циркуля и
линейки. Более того, полученные формулы указывают и конкретный способ: прежде
всего надо построить отрезки, равные действительным и мнимым частям комплексных
чисел 
, а затем
точки с соответствующими координатами – они и будут вершинами пятиугольника.
Заключение
Исследовав эту тему и проанализировав весь
материал, который смогли найти, мы сделали вывод, что комплексные уравнения не
только незаменимы, но и должны рассматриваться в широком спектре их
практического применения.
Метод комплексных чисел позволяет решать
планиметрические задачи по готовым формулам прямым вычислением, элементарными
выкладками. Выбор этих формул с очевидностью диктуется условиями задачи и ее
требованием. В этом состоит необычайная простота этого метода по сравнению с
координатным, векторным и другими методами, требующими от решающего порой
немалой сообразительности, длительных поисков, хотя готовое решение может быть
очень коротким.
Список использованной литературы
1.
«Энциклопедия для детей – математика» 1998 г.
.
«Энциклопедический словарь юного математика» 1997 г.
Этапное планирование
Этапный план составляют непосредственно перед началом очередного этапа с учётом пройденного и достигнутого на предыдущем этапе. В условиях учебных заведений этапные планы общего курса физического воспитания обычно составляют в расчёте на четверть или семестр учебного года.
Этапное планирование в спорте обычно имеет продолжительность от 1 – 1.5 до 2 – 2.5 месяца.
1. Поурочный рабочий план на четверть
– составляется на основе годового плана-графика учебного процесса для параллелей классов на каждую четверть. В нём в более конкретном виде, чем в годовом плане-графике, представлены используемые средства и отражена методика обучения двигательным действиям и воспитания физических качеств (Рабочий план на первую четверть для учащихся 6-го класса (таблица)).
Школьный рабочий план имеет две части: объяснительную записку и само содержание плана.
В объяснительной записке должны быть чётко определены и сформулированы задачи учебной работы на четверть с данной параллелью классов, указаны объёмы изучения нового материала; отмечены особенности организации и методики занятий в данной четверти, приведены контрольные упражнения, учебные нормативы и требования на четверть.
В рабочем плане приводятся основные изучаемые упражнения разделов программы, распределенные в порядке преемственности и постепенного усложнения поурочно. Кроме того, в рабочем плане отводится время (в минутах) на сообщение знаний по физической культуре, предусмотренных программой для данной параллели классов и исходя из общего объёма часов, отведённых на теоретический раздел.
Рабочие планы составляют в графической или текстовой формах.
В графическом учебном плане предусматривают следующие графы: «Учебный материал» и «Номера уроков».
В графе Учебный материал перечисляют разделы и подразделы учебного материала, запланированного на данную четверть.
В графе Номера уроков проставляют условными знаками то упражнение или тот теоретический материал, который планируется на данном уроке. Распределение изучаемых упражнений на каждом уроке в четверти отмечается следующими знаками: «Р» – разучивание, «З» – закрепление, «С» – совершенствование, «У» – учёт знаний, умений, навыков: показателей в контрольных упражнениях, тестах. Знак « » или « – « указывается использование этого материала на уроке.
В конце графического плана указываются контрольные упражнения и нормативы, соответствующие оценкам «хорошо» и «отлично» для мальчиков и для девочек.
2. Этапное планирование в спорте
В спортивной подготовке, когда число занятий в недельном цикле велико (двухразовые занятия в день) и они широко варьируются по содержанию, параметрам нагрузки, формам и внешним условиям организации, этапный план составляется с меньшей детализацией, определяя в основном содержание основной части занятий (Этапное планирование в спорте (таблица)).
Этапное планирование в спорте осуществляется, как правило, на 4 – 6 недель. В нём на каждую неделю планируются: суммарный объём нагрузки, число тренировочных дней, занятий, число дней соревнований (если они должны быть на этом этапе), определяются средства, направленность и величина нагрузок.
В соответствии с принципами регулирования динамики нагрузок, в рамках этапа требуется предусмотреть их увеличение и вместе с тем варьирование по микроциклам с тем, чтобы обеспечить развитие тренированности.
Краткосрочное (оперативное) планирование
1. Недельный (микроцикловой) план (таблица ниже).
Многие типы микроциклов в спортивной тренировке отличаются большим числом тренировочных занятий, а отсюда и высокой степенью концентрации тренирующих воздействий, разнообразием нагрузок по их направленности и величине, системе чередования их с отдыхом.
Микроцикловой план представляет собой план-график, в котором более детально и подробно планируются физические упражнения, направленность и величина нагрузок каждого занятия.
Для составления плана-графика микроцикла нужно предварительно выполнить соответствующие подготовительные операции:
• ориентируясь на контрольные показатели в предыдущих микроциклах, и соотнося их с этапной целью, конкретизировать целевую установку на предстоящий микроцикл;
• детализировать и уточнить перечень упражнений, предусмотренных в качестве основных и дополнительных средств целевой установки, наметить очерёдность и частоту их воспроизведения в данных занятиях на протяжении микроцикла;
• рассчитать параметры нагрузок, их динамику на протяжении микроцикла, ранжировать их по предлагаемой степени тренирующего воздействия.
2. План-конспект отдельного занятия – должен быть более конкретным из всех рассматриваемых документов планирования. Подробно урочная форма занятий и составление плана-конспекта были представлены в лекции: Урочные формы занятий.
План-график ударного микроцикла
Дни недели | Понедельник | Вторник | Среда | Четверг | Пятница | Суббота | Воскресенье |
Номера занятий | 1 2 | 3 4 | 5 6 | 7 8 | 9 10 | 11 12 | |
Направленность занятий и величина нагрузок в них | |||||||
1. Занятия избирательной направленности 1.1. Развитие аэробных, анаэробных, скоростных возможностей (Аэ, Ан, Ск – 2-з, 4-з, 5-з интенсивности) 1.1.1.Величина нагрузки (большая-Б, значительная-З) 1.2.Поддержание достигнутого уровня возможностей (Аэ, Ан, Ск – 1-з,2-з, 4-з, 5-з интенсивности) 1.2.1.Величина нагрузки (средняя-С, малая-М) | Ск-(5) З Ан-(4) С | Аэ-(1) М | Аэ-(2) Б Ск-(5) С | Аэ-(1) М | Аэ-(1) М | Ан-(4) З Аэ С | |
2. Занятия комплексной направленности 2.1.Развивающее воздействие в комплексных занятиях (Ск Ан; Ск Аэ; Ан Аэ или 5 4-з, 5 2-з, 4 2-з,) | Ан Ск Б | Аэ Ан З | Ск Ан Б | ||||
3. Затраты времени на занятия часов | 2 1.5 | 2.1 1 | 2 1,5 | 2.2 0,8 | 2 0,7 | 2 1,3 | Всего: 19,1 |
Примерный общий план работы по физическому воспитанию на учебный год в общеобразовательной школе
Основные разделы и содержание работы | Сроки проведения | Ответственные за выполнение |
1) Организационная работа 1. Составить и утвердить документы по физическому воспитанию: а) Годовой план-график; б) Поурочные планы на: Первую четверть Вторую четверть Третью четверть Четвёртую четверть 2. Обсудить на педсовете порядок проведения гимнастики до занятий, физкультминуток на уроках, подвижных игр на переменах 3. Определить каждому классу места для проведения гимнастики до занятий и подвижных игр на переменах 4. Провести беседы в классах о режиме дня школьника, о порядке проведения гимнастики до занятий, подвижных игр на переменах 5. Составить расписание занятий секций | Август Август Октябрь Декабрь Март Август Август До 10 сентября До 10 сентября | Учитель физической культуры Администрация, учитель физической культуры Учитель Ф. К. Классные руководители Учитель Ф. К. |
2) Учебная работа Проведение уроков физической культуры | 2 раза в неделю | Учитель Ф. К. |
3) Физкультурно-спортивные мероприятия в режиме учебного дня 1. Проведение гимнастики до занятий 2. Проведение подвижных игр и занятий физическими упражнениями на больших переменах 3. Проведение физкультминуток на общеобразовательных уроках в 1 – 4 классах 4. Проведение подвижных игр и занятий физическими упражнениями на больших переменах 5. Проведение физкультминуток на общеобразовательных уроках в 1 – 4 классах 6. Проведение занятий физическими упражнениями и игр в группах продлённого дня | Ежедневно Ежедневно Ежедневно Ежедневно Ежедневно Ежедневно | Инструкторы-общественники Инструкторы-общественники Учители и инструкторы-общественники Инструкторы-общественники Учители и инструкторы-общественники Воспитатель |
4) Физкультурно-массовая и спортивная работа во внеурочное время 1. Проведение физкультурного праздника, посвящённого началу учебного года 2. Проведение занятий в спортивных секциях и кружках 3. Проведение внутришкольной спартакиады учащихся 4. Участие в городской спартакиаде и соревнованиях по отдельным видам спорта 5. Проведение туристического слёта и соревнований по спортивному ориентированию | Сентябрь В течение года В течение года Согласно календарю соревнований Июнь | Администрация и учитель физической культуры Учитель Ф. К. Учитель Ф. К., классные руководители Учитель Ф. К. Учитель Ф. К., администрация |
5) Агитационно-пропагандистская работа 1. Оформление уголка физической культуры, стенда с призами, вымпелами, грамотами, стенда «Лучшие спортсмены школы» 2. Проведение спортивных вечеров, спортивных викторин, спортивного КВН . | Сентябрь Декабрь, май | Учитель Ф. К. Учитель Ф. К |
6) Врачебный контроль и медико-санитарный надзор 1. Проведение медицинского осмотра учащихся и распределение их по медицинским группам 2. Контроль за состоянием здоровья учащихся спецгрупп 3. Проведение итогового медицинского осмотра учащихся | Сентябрь Ежемесячно Май | Врач, администрация Врач Врач, администрация |
7) Хозяйственная работа 1. Ремонт спортивного инвентаря, оборудования 2. Изготовление наглядных пособий по физической культуре | В течение года В течение года | Учитель Ф. К. Учитель Ф. К. |
Один из вариантов годового плана-графика учебного процесса по физическому воспитанию для учащихся 5-го класса
Учебный материал | Количество уроков | Первая четверть | Вторая четверть Номера уроков 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18 | 19,20,21,22,23,24,25,26,27,28,29,30,31,32 |
Основы знаний | 5 | 1,2 | 1,2 |
Легкая атлетика | 18 | 1,2,3,4,5,6,7,8 | |
Баскетбол | 21 | 1,2,3,4,5,6,7,8,9,10 | |
Гимнастика | 14 | | 19,20,21,22,23,24,25,26,27,28,29,30,31,32 |
Лыжная подготовка | 15 | |
Подвижные игры | 33 | 1,2,3,4,5,6 | 19,20,21,22,23,24,25,26,27,28,29,30,31 |
Учебный материал | Количество уроков | Третья четверть | Четвёртая четверть Номера уроков 33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52 | 53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68 |
Основы знаний | 5 | 33 | |
Легкая атлетика | 18 | 33,34,35,36,37,38,39,40,41,42 | |
Баскетбол | 21 | 33,34,35,36,37 | 53,54,55,56,57,58 |
Гимнастика | 14 | |
Лыжная подготовка | 15 | 33,34,35,36,37,38,39,40,41,42,43,44,45,46,47 | |
Подвижные игры | 33 | 33,34,35,36,37,38 | 53,54,55,56,57,58,59,60 |
Рабочий план на первую четверть для учащихся 6-го класса
Учебный материал | Номера уроков |
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18 | |
Основы знаний Правила безопасности на полосе препятствий Содержание нового комплекса утренней гимнастики Строй Повторение упражнений 4-го класса Строевой шаг Общеразвивающие упражнения Специальные беговые упражнения Специальные прыжковые упражнения Линейные эстафеты с этапом 50 м. Преодоление полосы препятствий (4 – 5 препятствий) Упражнения в парах на сопротивление Упражнения со скакалками Упражнения с набивными мячами (гантелями) Упражнения типа зарядки Легкая атлетика Старт с опорой на одну руку Низкий старт Бег 60 м. с низкого старта Прыжки в длину с разбега Метание мяча 150 г. с четырёх-пяти шагов разбега Бег в умеренном темпе Баскетбол Ловля и передача мяча Передача мяча со сменой мест в тройке Ведение мяча шагом и бегом (прямо) Броски мяча после ведения по кольцу Учебные игры 3 * 3; 4* 4 по упрощённым правилам Игры Эстафеты с преодолением препятствий Эстафеты с предметами Эстафеты с элементами баскетбола «Перестрелка» Контроль двигательной подготовленности Бег 30 м. с высокого старта Прыжки в длину с места Подтягивания на перекладине Контрольные упражнения Бег 60 м. Метание мяча 150 г. с разбега Прыжки в длину с разбега Бег 1500 м Подтягивание на перекладине: Мальчики – высокая; Девочки – низкая | 1 1,2 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 17,18 1,2,3 4,5,6 3,4 7,8 9,10 11,12,13 14,15,16 17,18 с1 с2 р1 з2 с3 у4 у5 р3 з4 с5 у6 р4 з5 с6 у7 1,2,3,4,5,6,7,8 у с10 с11 с12 с10 с11 с12 р13 з14 с15 р13 з14 с15 15 16 17 1 2 13 14 12 13 14 15 16 17 18 у2 у3 р15 з16 с17 у18 Мальчики | Девочки 9,8 – 10,4 – 11,1 | 10,3 – 10,6 – 11,2 36 – 29 21 | 23 – 18 – 15 360 – 330 – 270 см. | 330 – 280 – 230 7.30 – 7.50 – 8.10 мин. | 8.00 – 8.20 – 8.40 мин. 7 – 5 – 4 раза | 17 – 14 – 9 раз. |
Условные обозначения:
Знак указывает на использование этого материала на уроке;
«Р» – разучивание двигательного действия;
«З» – закрепление двигательного действия;
«С» – совершенствование двигательного действия;
«У» – учёт знаний, умений, навыков, показателей в контрольных тестах.
