- Исходные данные
- 2. Практическая часть
- 1 Проверка гипотезы о точности настройки до ремонта и после ремонта
- 2 Проверка точности настройки в зависимости от номинала
- .3 вычисление доли брака при различных настройках, которая может быть использована как годная продукция другого сорта (номинала)
- 4 Определение количества замеров толщины стенки листа стали для уверенности в статистических выводах
- Заключение
- Список литературы
- 1 Проверка гипотезы о точности настройки до ремонта и после ремонта
- 2 Проверка точности настройки в зависимости от номинала
- .3 вычисление доли брака при различных настройках, которая может быть использована как годная продукция другого сорта (номинала)
- 4 Определение количества замеров толщины стенки листа стали для уверенности в статистических выводах
- Заключение
- Список литературы
Исходные данные
статистический анализ технологический
В одном из цехов анализируется работа листопрокатного стана по
результатам контроля качества продукции. Основным показателем качества является
толщина Xj (мм) готового листа. Целью исследования является
выяснение вопроса: достаточно ли проводить только настройку технологического
процесса или необходимо уже проводить ремонт и замену оборудования для
обеспечения заданной точности по толщине металла.
Кроме того, попутно решается
вопрос, какая доля брака может быть пущена как годная продукция другого сорта
(другой толщины листа). Исследуемая номинальная толщина листа 1,9 мм (допуск
±0,04 мм); 2,0 мм (допуск ±0,04 мм); 2,1 мм (допуск ±0,05 мм).
Сформулируйте и проверьте статистические гипотезы, необходимые для ответа
на вопросы:
• Существенно ли разнится точность
настройки процесса до ремонта и после ремонта?
• Существенно ли разнится точность
настройки в зависимости от того номинала, на который ведется настройка?
• Какая доля брака при различных
настройках может быть использована как годная продукция другого сорта
(номинала)?
• Сколько замеров толщины стенки листа
стали необходимо провести, чтобы быть уверенными в статистических выводах?
Таблица 26 – Настройка сразу после ремонта; N1 = 145 (номинал
2 мм)
Xj,мм | 1,93 | 1,94 | 1,95 | 1,96 | 1,97 | 1,98 | 1,99 | 2,01 | 2,03 | 2,05 | 2,06 | 2,08 | 2,10 |
nj | 2 | 3 | 3 | 7 | 10 | 20 | 23 | 30 | 28 | 13 | 4 | 1 | 1 |
Таблица 27 – Настройка без проведения ремонта; N2 = 115
(номинал 2 мм)
Xj,мм1,901,921,961,971,982,002,022,042,052,062,072,092,10 | |||||||||||||
nj | 2 | 1 | 3 | 7 | 12 | 20 | 25 | 17 | 7 | 10 | 7 | 3 | 1 |
Таблица 28 – Настройка сразу после ремонта; N3 = 105 (номинал
1,9 мм)
Xj,мм | 1,85 | 1,86 | 1,87 | 1,89 | 1,90 | 1,91 | 1,92 | 1,93 | 1,94 | 1,95 | 1,96 |
nj | 1 | 6 | 5 | 20 | 25 | 15 | 20 | 5 | 4 | 3 | 1 |
Таблица 29 – Настройка без проведения ремонта; N4 = 76
(номинал 1,9 мм)
Xj,мм | 1,85 | 1,87 | 1,89 | 1,91 | 1,92 | 1,93 | 1,94 | 1,96 | 1,97 | 1,98 |
nj | 1 | 2 | 10 | 10 | 27 | 10 | 6 | 5 | 4 | 1 |
Таблица 30 – Настройка сразу после ремонта; N5 = 30 (номинал
2,1 мм)
Xj,мм | 2,04 | 2,06 | 2,08 | 2,09 | 2,10 | 2,11 | 2,12 | 2,14 |
nj | 1 | 1 | 2 | 4 | 10 | 8 | 3 | 1 |
Таблица 31 – Настройка без проведения ремонта; N6 = 29
(номинал 2,1 мм)
Xj,мм | 2,04 | 2,06 | 2,08 | 2,09 | 2,10 | 2,11 | 2,12 | 2,13 | 2,14 | 2,16 |
nj | 1 | 1 | 2 | 1 | 3 | 4 | 8 | 1 | 7 | 1 |
Уровень значимости α: 0,05; 0,025.
Точность вычислений (число знаков после запятой): 3.
2.
Практическая часть
1 Проверка гипотезы о точности настройки до ремонта и
после ремонта
Для проверки гипотезы о степени различимости точности настройки до
ремонта и после ремонта воспользуемся следующими рекомендациями для сравнения
двух выборочных средних значений для независимых выборок.
Порядок применения:
. Принимается предположение о нормальности, формулируются гипотеза
Н0 и альтернатива Н1, задается уровень значимости.
. Вычисляются выборочные характеристики х, Sx и у, Sy.
. Используется F-критерий для проверки гипотезы о равенстве
генеральных дисперсий.
. По результатам применения F-критерия принимается или не
принимается предположение о равенстве дисперсий.
. Вычисляются значение t-критерия и число степеней свободы n.
. Из таблицы t-распределения Стьюдента находится – критическое
значение t-критерия при заданном уровне значимости а и числе степеней свободы
n.
. Делается вывод: если tнабл ≥ tкрит,
то выборочные средние значимо различаются на уровне значимости a (вероятность
ошибки меньше a). В противном случае различие статистически незначимо.
Алгоритм решения задачи:
. Предположение о нормальности распределения выборок X и Y будем
делать с помощью критерия Пирсона.
Начнем с гистограмм, отображающих толщину прокатного листа до и после
ремонта. Для каждой толщины листа по отдельности. По внешнему виду гистограммы
одномодальные, куполообразные и в первом приближении можно считать, что они
характеризует нормальный закон распределения.
Оценка параметров распределения
Определим оценки среднего и среднеквадратичного отклонения. Воспользуемся
для этого “табличным” методом. Исходные расчетные таблицы для 6
выборок:
Настройка сразу после ремонта; N1 = 145 (номинал 2 мм)
Xi | N | Nxi | Nxi2 |
1,93 | 2 | 3,86 | 7,4498 |
1,94 | 3 | 5,82 | 11,2908 |
1,95 | 3 | 5,85 | 11,4075 |
1,96 | 7 | 13,72 | 26,8912 |
1,97 | 10 | 19,7 | 38,809 |
1,98 | 20 | 39,6 | 78,408 |
1,99 | 23 | 45,77 | 91,0823 |
2,01 | 30 | 60,3 | 121,203 |
2,03 | 28 | 56,84 | 115,3852 |
2,05 | 13 | 26,65 | 54,6325 |
2,06 | 4 | 8,24 | 16,9744 |
2,08 | 1 | 2,08 | 4,3264 |
2,1 | 1 | 2,1 | 4,41 |
Итого: | 145 | 290,53 | 582,2701 |
Среднее значение можно оценить как
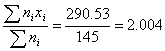
Среднее
квадратичное отклонение как:
![]()
Настройка
без проведения ремонта; N2 = 115 (номинал 2 мм)
Xi | N | Nxi | Nxi2 |
1,9 | 2 | 3,8 | 7,22 |
1,92 | 1 | 1,92 | 3,6864 |
1,96 | 3 | 5,88 | 11,5248 |
1,97 | 7 | 13,79 | 27,1663 |
1,98 | 12 | 23,76 | 47,0448 |
2 | 20 | 40 | 80 |
2,02 | 25 | 50,5 | 102,01 |
2,04 | 17 | 34,68 | 70,7472 |
2,06 | 7 | 14,42 | 29,7052 |
2,07 | 10 | 20,7 | 42,849 |
2,09 | 7 | 14,63 | 30,5767 |
2,1 | 3 | 6,3 | 13,23 |
2,1 | 1 | 2,1 | 4,41 |
115 | 232,48 | 470,1704 |
Среднее значение можно оценить как
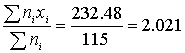
Среднее
квадратичное отклонение как:
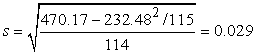
Настройка
сразу после ремонта; N3 = 105 (номинал 1,9 мм)
Xi | N | Nxi | Nxi2 |
1,85 | 1 | 1,85 | 3,4225 |
1,86 | 6 | 11,16 | 20,7576 |
1,87 | 5 | 9,35 | 17,4845 |
1,89 | 20 | 37,8 | 71,442 |
1,9 | 25 | 47,5 | 90,25 |
1,91 | 15 | 28,65 | 54,7215 |
1,92 | 38,4 | 73,728 | |
1,93 | 5 | 9,65 | 18,6245 |
1,94 | 4 | 7,76 | 15,0544 |
1,95 | 3 | 5,85 | 11,4075 |
1,96 | 1 | 1,96 | 3,8416 |
Итого | 105 | 199,93 | 380,7341 |
Среднее значение можно оценить как
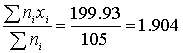
Среднее
квадратичное отклонение как:
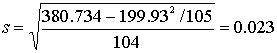
Настройка
без проведения ремонта; N4 = 76 (номинал 1,9 мм)
Xi | N | Nxi | Nxi^2 |
1,85 | 1 | 1,85 | 3,4225 |
1,87 | 2 | 3,74 | 6,9938 |
1,89 | 10 | 18,9 | 35,721 |
1,91 | 10 | 19,1 | 36,481 |
1,92 | 27 | 51,84 | 99,5328 |
1,93 | 10 | 19,3 | 37,249 |
1,94 | 6 | 11,64 | 22,5816 |
1,96 | 5 | 9,8 | 19,208 |
1,97 | 4 | 7,88 | 15,5236 |
1,98 | 1 | 1,98 | 3,9204 |
Итого | 76 | 146,03 | 280,6337 |
Среднее значение можно оценить как
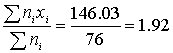
Среднее
квадратичное отклонение как:
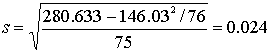
Настройка
сразу после ремонта; N5 = 30 (номинал 2,1 мм)
Xi | N | Nxi | Nxi^2 |
2,04 | 1 | 2,04 | 4,1616 |
2,06 | 1 | 2,06 | 4,2436 |
2,08 | 2 | 4,16 | 8,6528 |
2,09 | 4 | 8,36 | 17,4724 |
2,1 | 10 | 21 | 44,1 |
2,11 | 8 | 16,88 | 35,6168 |
2,12 | 3 | 6,36 | 13,4832 |
2,14 | 1 | 2,14 | 4,5796 |
Итого | 30 | 63 | 132,31 |
Среднее значение можно оценить как
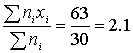
Среднее
квадратичное отклонение как:
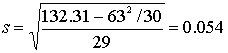
Настройка
без проведения ремонта; N6 = 29 (номинал 2,1 мм)
Xi | N | Nxi | Nxi^2 |
2,4 | 1 | 2,4 | 5,76 |
2,06 | 1 | 2,06 | 4,2436 |
2,08 | 2 | 4,16 | 8,6528 |
2,09 | 1 | 2,09 | 4,3681 |
2,1 | 3 | 6,3 | 13,23 |
2,11 | 4 | 8,44 | 17,8084 |
2,12 | 8 | 16,96 | 35,9552 |
2,13 | 1 | 2,13 | 4,5369 |
2,14 | 7 | 14,98 | 32,0572 |
2,16 | 1 | 2,16 | 4,6656 |
Итого | 29 | 61,68 | 131,2778 |
Среднее значение можно оценить как
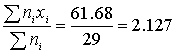
Среднее
квадратичное отклонение как:

Таким
образом, можно сделать выводы, что рассматриваемые нами распределения
вероятности подчиняется нормальному закону распределения.
Необходимо
сформулировать две альтернативных гипотезы. Во-первых, можно предположить,
точность настройки до и после ремонта не существенно различаются. Эта гипотеза
называется нулевой гипотезой (H0). Альтернативная гипотеза (H1),
состоит в том, точность настройки до и после ремонта различаются существенно.
Выпишем
несмещенные оценки генеральной дисперсии по формуле:
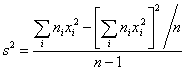
![]()
![]()
![]()
![]()
![]()
![]()
Для
проверки 0-гипотезы о равенстве генеральных дисперсий используется F-критерий
Фишера. На уровне значимости q 0-гипотеза имеет место, если отношение
выборочных дисперсий лежит в квантильных границах:
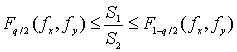
Выполнение
соотношения говорит о том, что можно принять 0-гипотезу. Если полученное на
практике отношение выборочных дисперсий выходит за левую границу этого
интервала, то нужно принять альтернативную гипотезу Sx<Sy.
А выход отношения выборочных дисперсий за правую границу − это область
альтернативной гипотезы Sx>Sy.
Толщина
листа 2 мм:
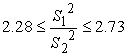
![]()
Неравенство
выполняется, значит мы можем принять гипотезу Н0 о равенстве
генеральных дисперсий.
Толщина
листа 1,9 мм
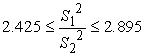
![]()
Неравенство
выполняется, значит мы можем принять гипотезу Н0 о равенстве
генеральных дисперсий.
Толщина
листа 2,1 мм
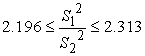
![]()
Неравенство
выполняется, значит мы можем принять гипотезу Н0 о равенстве
генеральных дисперсий.
Теперь
вычисляются значение t-критерия и число степеней свободы n.
Толщина
листа 2 мм
Результат:
tЭмп = 4.7
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.96 | 2.58 |
Полученное эмпирическое значение t (4.7) находится в зоне значимости.
Это означает, что при толщине 2 мм точность настройки до и после ремонта
меняется незначительно.
Толщина листа 1,9 мм:
Результат: tЭмп = 4.9
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.97 | 2.61 |
Полученное эмпирическое значение t (4.9) находится в зоне значимости.
Это означает, что при толщине 1,9 мм точность настройки до и после
ремонта меняется незначительно.
Толщина листа 2,1 мм:
Результат: tЭмп = 1.7
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
2 | 2.66 |
Полученное эмпирическое значение t (1.7) находится в зоне незначимости.
Это означает, что при толщине 2,1 мм точность настройки до и после
ремонта меняется значительно.
2 Проверка точности настройки в зависимости от номинала
Для формулирования и проверки гипотез о точности настройки в зависимости
от номинала необходимо вычислить разницу между значениями толщины и усредненным
значением.
Толщина 2.1 мм:
Xi | N | xi-xср | (xi-xср)*N | (xi-xср)2*N |
2,4 | 1 | 0,3 | 0,3 | 0,09 |
2,06 | 1 | 0,04 | 0,04 | 0,0016 |
2,08 | 2 | 0,02 | 0,04 | 0,0008 |
2,09 | 1 | 0,01 | 0,01 | 0,0001 |
2,1 | 3 | 0 | 0 | 0 |
2,11 | 4 | 0,01 | 0,04 | 0,0004 |
2,12 | 8 | 0,02 | 0,16 | 0,0032 |
2,13 | 1 | 0,03 | 0,03 | 0,0009 |
2,14 | 7 | 0,04 | 0,28 | 0,0112 |
2,16 | 1 | 0,06 | 0,06 | 0,0036 |
Итого | 29 | 0,53 | 0,96 | 0,1118 |
Среднее значение отклонения можно оценить как
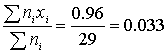
Среднее
квадратичное отклонение как
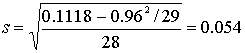
Толщина
1.9 мм:
XiNxi-xср(xi-xср)*N(xi-xср)2*N | ||||
1,85 | 1 | 0,07 | 0,07 | 0,0049 |
1,87 | 2 | 0,05 | 0,1 | 0,005 |
1,89 | 10 | 0,03 | 0,3 | 0,009 |
1,91 | 10 | 0,01 | 0,1 | 0,001 |
1,92 | 27 | 0 | 0 | 0 |
1,93 | 10 | 0,01 | 0,1 | 0,001 |
1,94 | 6 | 0,02 | 0,12 | 0,0024 |
1,96 | 5 | 0,04 | 0,2 | 0,008 |
1,97 | 4 | 0,05 | 0,2 | 0,01 |
1,98 | 1 | 0,06 | 0,06 | 0,0036 |
Итого | 76 | 1,25 | 0,0449 |
Среднее значение отклонения можно оценить как
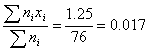
Среднее
квадратичное отклонение как
![]()
Толщина
2.0 мм:
Xi | N | xi-xср | (xi-xср)*N | (xi-xср)2*N |
1,9 | 2 | 0,121 | 0,242 | 0,029282 |
1,92 | 1 | 0,101 | 0,101 | 0,010201 |
1,96 | 3 | 0,061 | 0,183 | 0,011163 |
1,97 | 7 | 0,051 | 0,357 | 0,018207 |
1,98 | 12 | 0,041 | 0,492 | 0,020212 |
2 | 20 | 0,021 | 0,42 | 0,00882 |
2,02 | 25 | 0,001 | 0,025 | 2,5E-05 |
2,04 | 17 | 0,019 | 0,323 | 0,006137 |
2,05 | 7 | 0,029 | 0,203 | 0,005887 |
2,06 | 10 | 0,039 | 0,39 | 0,01521 |
2,07 | 7 | 0,049 | 0,343 | 0,016807 |
2,09 | 3 | 0,069 | 0,207 | 0,014283 |
2,1 | 1 | 0,079 | 0,079 | 0,006241 |
Итого | 115 | 0,681 | 3,365 | 0,162435 |
Среднее значение отклонения можно оценить как
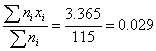
Среднее
квадратичное отклонение как
![]()
Необходимо
сформулировать две альтернативных гипотезы. Во-первых, можно предположить,
точность настройки не существенно различаются в зависимости от номинала. Эта
гипотеза называется нулевой гипотезой (H0). Альтернативная гипотеза
(H1), состоит в том, точность настройки различаются существенно в
зависимости от номинала.
Выпишем
несмещенные оценки генеральной дисперсии по формуле:
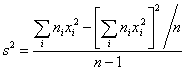
![]()
![]()
![]()
Для
проверки 0-гипотезы о равенстве генеральных дисперсий используется F-критерий
Фишера. На уровне значимости q 0-гипотеза имеет место, если отношение
выборочных дисперсий лежит в квантильных границах:
Чтобы
сравнить все 3 номинала, необходимо выполнить 3 оценки по критерию Фишера
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Выполнение
соотношения говорит о том, что можно принять 0-гипотезу. Если полученное на
практике отношение выборочных дисперсий выходит за левую границу этого
интервала, то нужно принять альтернативную гипотезу Sx<Sy.
А выход отношения выборочных дисперсий за правую границу − это область
альтернативной гипотезы Sx>Sy.
Теперь
вычисляются значение t-критерия и число степеней свободы n.
Сравнение
2.0 мм толщины и 1.9 мм толщины
Результат:
tЭмп = 1.6
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
2.08 | 2.83 |
Полученное эмпирическое значение t (1.6) находится в зоне незначимости.
Это означает, что при сравнении точности настройки номинала 2,0 мм и 1.9
мм точность настройки в зависимости от номинала отличается значительно.
Сравнение 2.0 мм толщины и 2.1 мм толщины.
Результат: tЭмп = 2.8
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.97 | 2.61 |
Полученное эмпирическое значение t (2.8) находится в зоне значимости.
Это означает, что при сравнении точности настройки номинала 2,0 мм и 2,1
мм точность настройки в зависимости от номинала отличается незначительно.
Сравнение 1,9 мм толщины и 2,1 мм толщины.
Результат: tЭмп = 1.3
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.98 | 2.63 |
Полученное эмпирическое значение t (1.3) находится в зоне незначимости.
Это означает, что при сравнении точности настройки номинала 1.9 мм и 2.1
мм точность настройки в зависимости от номинала отличается значительно.
.3 вычисление доли брака при различных настройках, которая
может быть использована как годная продукция другого сорта (номинала)
Для номинала 2 мм
Определяем долю годной продукции:
![]()
![]()
С
помощью таблицы функции нормального распределения получим
![]()
Доля
дефектной продукции
![]() , в
, в
процентах 2.78%
Из
них 2,02 % может быть пушена как годная продукция другого сорта.
Для
номинала 1,9 мм
Определяем
долю годной продукции:
![]()
![]()
С
помощью таблицы функции нормального распределения получим
![]()
Доля
дефектной продукции
![]() , в
, в
процентах 1.79%
Из
них 1,00 % может быть пушена как годная продукция другого сорта
Для
номинала 2,1 мм
Определяем
долю годной продукции:
![]()
![]()
С
помощью таблицы функции нормального распределения получим
![]()
Доля
дефектной продукции
![]() , в
, в
процентах 1.14%
Из
них 0,76 % может быть пушена как годная продукция другого сорта
4 Определение количества замеров толщины стенки листа стали
для уверенности в статистических выводах
Для того чтобы быть уверенным в статистических выводах, вероятность того,
что толщина листа попадает в интервал с заданными значениями должна быть не
меньше 95%. Отклонение величины от заданной вероятности должно быть не более
0,05.
Для 2 мм толщины:
мм-0,04<Толщина листа<2 мм 0,04
Для 1,9 мм толщины:
мм-0,05<Толщина листа<2 мм 0,05
Для 2,1 мм толщины:
мм-0,04<Толщина листа<2 мм 0,04
В предыдущем пункте мы уже определили, какова вероятность листов каждой
толщины считаются пригодными для использования:
Получились следующие данные:
мм: 97,22%
,9 мм 98,19%
,1 мм: 98,86%
Нужно,
чтобы условие ![]() выполнялось с вероятностью 0,95. Раскроем модуль и
выполнялось с вероятностью 0,95. Раскроем модуль и
найдем границы для m:
,65n<
m < 0,75n. По теореме Муавра – Лапласа:
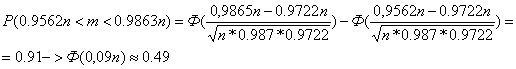
По
таблице находим
![]() n=129
n=129
Для
1,9 мм толщины:
Нужно,
чтобы условие ![]() выполнялось с вероятностью 0,95. Раскроем модуль и
выполнялось с вероятностью 0,95. Раскроем модуль и
найдем границы для m:
,9715n<
m < 0,9956n. По теореме Муавра – Лапласа:
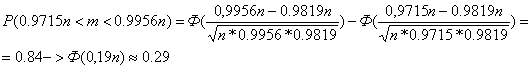
По
таблице находим
![]() n=65
n=65
Для
2,1 мм толщины:
Нужно,
чтобы условие ![]() выполнялось с вероятностью 0,95. Раскроем модуль и
выполнялось с вероятностью 0,95. Раскроем модуль и
найдем границы для m:
,9806n<
m < 0,9896n. По теореме Муавра – Лапласа:
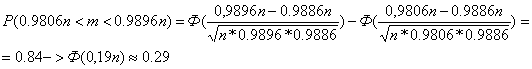
По
таблице находим
![]() n=27
n=27
Заключение
Проверка статистических гипотез – необходимая методика, используемая для
получения данных в статистике.
Проведенная работа позволила сделать следующие выводы:
· Под статистической гипотезой понимаются различного рода
предположения относительно характера или параметров распределения случайной
переменной, которые можно проверить, опираясь на результаты наблюдений в
случайной выборке.
· Смысл проверки статистической гипотезы состоит в том, чтобы
по имеющимся статистическим данным принять или отклонить статистическую
гипотезу с минимальным риском ошибки. Эта проверка осуществляется по
определенным правилам.
Анализируя результаты работы можно ответить на поставленный вопрос:
достаточно ли проводить только настройку технологического процесса или необходимо
уже проводить ремонт и замену оборудования для обеспечения заданной точности по
толщине металла.
Проведя все необходимые вычисления, мы пришли к выводу, что на данном
этапе достаточно проводить лишь настройку техпроцесса для каждого номинала.
Список литературы
статистический анализ технологический
1. Вентцель Е.С. Теория вероятностей. М., Высшая школа,
2002.
. Гмурман В.Е. Руководство к решению задач по теории
вероятностей и математической статистике. М., Высшая школа, 2004.
. Гмурман В.Е. Теория вероятностей и математическая
статистика. М., Высшая школа, 2003.
. Емельянов Г.В., Скитович В.П. Задачник по теории
вероятностей и математической статистике. М., Изд. МГУ, 1967.
. Коваленко И.Н., Филиппова А.А. Теория вероятностей и
математическая статистика. М, Высшая школа, 1982.
. Корн Г., Корн Т. Справочник по математике для
научных работников и инженеров. М., Наука, 1978.
1 Проверка гипотезы о точности настройки до ремонта и
после ремонта
Для проверки гипотезы о степени различимости точности настройки до
ремонта и после ремонта воспользуемся следующими рекомендациями для сравнения
двух выборочных средних значений для независимых выборок.
Порядок применения:
. Принимается предположение о нормальности, формулируются гипотеза
Н0 и альтернатива Н1, задается уровень значимости.
. Вычисляются выборочные характеристики х, Sx и у, Sy.
. Используется F-критерий для проверки гипотезы о равенстве
генеральных дисперсий.
. По результатам применения F-критерия принимается или не
принимается предположение о равенстве дисперсий.
. Вычисляются значение t-критерия и число степеней свободы n.
. Из таблицы t-распределения Стьюдента находится – критическое
значение t-критерия при заданном уровне значимости а и числе степеней свободы
n.
. Делается вывод: если tнабл ≥ tкрит,
то выборочные средние значимо различаются на уровне значимости a (вероятность
ошибки меньше a). В противном случае различие статистически незначимо.
Алгоритм решения задачи:
. Предположение о нормальности распределения выборок X и Y будем
делать с помощью критерия Пирсона.
Начнем с гистограмм, отображающих толщину прокатного листа до и после
ремонта. Для каждой толщины листа по отдельности. По внешнему виду гистограммы
одномодальные, куполообразные и в первом приближении можно считать, что они
характеризует нормальный закон распределения.
Оценка параметров распределения
Определим оценки среднего и среднеквадратичного отклонения. Воспользуемся
для этого “табличным” методом. Исходные расчетные таблицы для 6
выборок:
Настройка сразу после ремонта; N1 = 145 (номинал 2 мм)
Xi | N | Nxi | Nxi2 |
1,93 | 2 | 3,86 | 7,4498 |
1,94 | 3 | 5,82 | 11,2908 |
1,95 | 3 | 5,85 | 11,4075 |
1,96 | 7 | 13,72 | 26,8912 |
1,97 | 10 | 19,7 | 38,809 |
1,98 | 20 | 39,6 | 78,408 |
1,99 | 23 | 45,77 | 91,0823 |
2,01 | 30 | 60,3 | 121,203 |
2,03 | 28 | 56,84 | 115,3852 |
2,05 | 13 | 26,65 | 54,6325 |
2,06 | 4 | 8,24 | 16,9744 |
2,08 | 1 | 2,08 | 4,3264 |
2,1 | 1 | 2,1 | 4,41 |
Итого: | 145 | 290,53 | 582,2701 |
Среднее значение можно оценить как
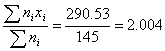
Среднее
квадратичное отклонение как:
![]()
Настройка
без проведения ремонта; N2 = 115 (номинал 2 мм)
Xi | N | Nxi | Nxi2 |
1,9 | 2 | 3,8 | 7,22 |
1,92 | 1 | 1,92 | 3,6864 |
1,96 | 3 | 5,88 | 11,5248 |
1,97 | 7 | 13,79 | 27,1663 |
1,98 | 12 | 23,76 | 47,0448 |
2 | 20 | 40 | 80 |
2,02 | 25 | 50,5 | 102,01 |
2,04 | 17 | 34,68 | 70,7472 |
2,06 | 7 | 14,42 | 29,7052 |
2,07 | 10 | 20,7 | 42,849 |
2,09 | 7 | 14,63 | 30,5767 |
2,1 | 3 | 6,3 | 13,23 |
2,1 | 1 | 2,1 | 4,41 |
115 | 232,48 | 470,1704 |
Среднее значение можно оценить как
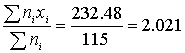
Среднее
квадратичное отклонение как:
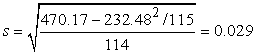
Настройка
сразу после ремонта; N3 = 105 (номинал 1,9 мм)
Xi | N | Nxi | Nxi2 |
1,85 | 1 | 1,85 | 3,4225 |
1,86 | 6 | 11,16 | 20,7576 |
1,87 | 5 | 9,35 | 17,4845 |
1,89 | 20 | 37,8 | 71,442 |
1,9 | 25 | 47,5 | 90,25 |
1,91 | 15 | 28,65 | 54,7215 |
1,92 | 38,4 | 73,728 | |
1,93 | 5 | 9,65 | 18,6245 |
1,94 | 4 | 7,76 | 15,0544 |
1,95 | 3 | 5,85 | 11,4075 |
1,96 | 1 | 1,96 | 3,8416 |
Итого | 105 | 199,93 | 380,7341 |
Среднее значение можно оценить как
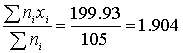
Среднее
квадратичное отклонение как:
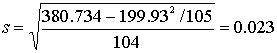
Настройка
без проведения ремонта; N4 = 76 (номинал 1,9 мм)
Xi | N | Nxi | Nxi^2 |
1,85 | 1 | 1,85 | 3,4225 |
1,87 | 2 | 3,74 | 6,9938 |
1,89 | 10 | 18,9 | 35,721 |
1,91 | 10 | 19,1 | 36,481 |
1,92 | 27 | 51,84 | 99,5328 |
1,93 | 10 | 19,3 | 37,249 |
1,94 | 6 | 11,64 | 22,5816 |
1,96 | 5 | 9,8 | 19,208 |
1,97 | 4 | 7,88 | 15,5236 |
1,98 | 1 | 1,98 | 3,9204 |
Итого | 76 | 146,03 | 280,6337 |
Среднее значение можно оценить как
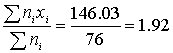
Среднее
квадратичное отклонение как:
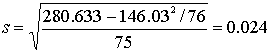
Настройка
сразу после ремонта; N5 = 30 (номинал 2,1 мм)
Xi | N | Nxi | Nxi^2 |
2,04 | 1 | 2,04 | 4,1616 |
2,06 | 1 | 2,06 | 4,2436 |
2,08 | 2 | 4,16 | 8,6528 |
2,09 | 4 | 8,36 | 17,4724 |
2,1 | 10 | 21 | 44,1 |
2,11 | 8 | 16,88 | 35,6168 |
2,12 | 3 | 6,36 | 13,4832 |
2,14 | 1 | 2,14 | 4,5796 |
Итого | 30 | 63 | 132,31 |
Среднее значение можно оценить как
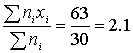
Среднее
квадратичное отклонение как:
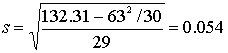
Настройка
без проведения ремонта; N6 = 29 (номинал 2,1 мм)
Xi | N | Nxi | Nxi^2 |
2,4 | 1 | 2,4 | 5,76 |
2,06 | 1 | 2,06 | 4,2436 |
2,08 | 2 | 4,16 | 8,6528 |
2,09 | 1 | 2,09 | 4,3681 |
2,1 | 3 | 6,3 | 13,23 |
2,11 | 4 | 8,44 | 17,8084 |
2,12 | 8 | 16,96 | 35,9552 |
2,13 | 1 | 2,13 | 4,5369 |
2,14 | 7 | 14,98 | 32,0572 |
2,16 | 1 | 2,16 | 4,6656 |
Итого | 29 | 61,68 | 131,2778 |
Среднее значение можно оценить как
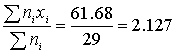
Среднее
квадратичное отклонение как:

Таким
образом, можно сделать выводы, что рассматриваемые нами распределения
вероятности подчиняется нормальному закону распределения.
Необходимо
сформулировать две альтернативных гипотезы. Во-первых, можно предположить,
точность настройки до и после ремонта не существенно различаются. Эта гипотеза
называется нулевой гипотезой (H0). Альтернативная гипотеза (H1),
состоит в том, точность настройки до и после ремонта различаются существенно.
Выпишем
несмещенные оценки генеральной дисперсии по формуле:
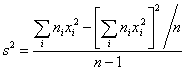
![]()
![]()
![]()
![]()
![]()
![]()
Для
проверки 0-гипотезы о равенстве генеральных дисперсий используется F-критерий
Фишера. На уровне значимости q 0-гипотеза имеет место, если отношение
выборочных дисперсий лежит в квантильных границах:
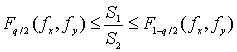
Выполнение
соотношения говорит о том, что можно принять 0-гипотезу. Если полученное на
практике отношение выборочных дисперсий выходит за левую границу этого
интервала, то нужно принять альтернативную гипотезу Sx<Sy.
А выход отношения выборочных дисперсий за правую границу − это область
альтернативной гипотезы Sx>Sy.
Толщина
листа 2 мм:
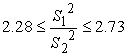
![]()
Неравенство
выполняется, значит мы можем принять гипотезу Н0 о равенстве
генеральных дисперсий.
Толщина
листа 1,9 мм
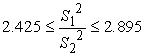
![]()
Неравенство
выполняется, значит мы можем принять гипотезу Н0 о равенстве
генеральных дисперсий.
Толщина
листа 2,1 мм
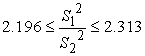
![]()
Неравенство
выполняется, значит мы можем принять гипотезу Н0 о равенстве
генеральных дисперсий.
Теперь
вычисляются значение t-критерия и число степеней свободы n.
Толщина
листа 2 мм
Результат:
tЭмп = 4.7
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.96 | 2.58 |
Полученное эмпирическое значение t (4.7) находится в зоне значимости.
Это означает, что при толщине 2 мм точность настройки до и после ремонта
меняется незначительно.
Толщина листа 1,9 мм:
Результат: tЭмп = 4.9
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.97 | 2.61 |
Полученное эмпирическое значение t (4.9) находится в зоне значимости.
Это означает, что при толщине 1,9 мм точность настройки до и после
ремонта меняется незначительно.
Толщина листа 2,1 мм:
Результат: tЭмп = 1.7
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
2 | 2.66 |
Полученное эмпирическое значение t (1.7) находится в зоне незначимости.
Это означает, что при толщине 2,1 мм точность настройки до и после
ремонта меняется значительно.
2 Проверка точности настройки в зависимости от номинала
Для формулирования и проверки гипотез о точности настройки в зависимости
от номинала необходимо вычислить разницу между значениями толщины и усредненным
значением.
Толщина 2.1 мм:
Xi | N | xi-xср | (xi-xср)*N | (xi-xср)2*N |
2,4 | 1 | 0,3 | 0,3 | 0,09 |
2,06 | 1 | 0,04 | 0,04 | 0,0016 |
2,08 | 2 | 0,02 | 0,04 | 0,0008 |
2,09 | 1 | 0,01 | 0,01 | 0,0001 |
2,1 | 3 | 0 | 0 | 0 |
2,11 | 4 | 0,01 | 0,04 | 0,0004 |
2,12 | 8 | 0,02 | 0,16 | 0,0032 |
2,13 | 1 | 0,03 | 0,03 | 0,0009 |
2,14 | 7 | 0,04 | 0,28 | 0,0112 |
2,16 | 1 | 0,06 | 0,06 | 0,0036 |
Итого | 29 | 0,53 | 0,96 | 0,1118 |
Среднее значение отклонения можно оценить как
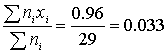
Среднее
квадратичное отклонение как
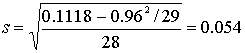
Толщина
1.9 мм:
XiNxi-xср(xi-xср)*N(xi-xср)2*N | ||||
1,85 | 1 | 0,07 | 0,07 | 0,0049 |
1,87 | 2 | 0,05 | 0,1 | 0,005 |
1,89 | 10 | 0,03 | 0,3 | 0,009 |
1,91 | 10 | 0,01 | 0,1 | 0,001 |
1,92 | 27 | 0 | 0 | 0 |
1,93 | 10 | 0,01 | 0,1 | 0,001 |
1,94 | 6 | 0,02 | 0,12 | 0,0024 |
1,96 | 5 | 0,04 | 0,2 | 0,008 |
1,97 | 4 | 0,05 | 0,2 | 0,01 |
1,98 | 1 | 0,06 | 0,06 | 0,0036 |
Итого | 76 | 1,25 | 0,0449 |
Среднее значение отклонения можно оценить как
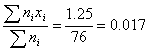
Среднее
квадратичное отклонение как
![]()
Толщина
2.0 мм:
Xi | N | xi-xср | (xi-xср)*N | (xi-xср)2*N |
1,9 | 2 | 0,121 | 0,242 | 0,029282 |
1,92 | 1 | 0,101 | 0,101 | 0,010201 |
1,96 | 3 | 0,061 | 0,183 | 0,011163 |
1,97 | 7 | 0,051 | 0,357 | 0,018207 |
1,98 | 12 | 0,041 | 0,492 | 0,020212 |
2 | 20 | 0,021 | 0,42 | 0,00882 |
2,02 | 25 | 0,001 | 0,025 | 2,5E-05 |
2,04 | 17 | 0,019 | 0,323 | 0,006137 |
2,05 | 7 | 0,029 | 0,203 | 0,005887 |
2,06 | 10 | 0,039 | 0,39 | 0,01521 |
2,07 | 7 | 0,049 | 0,343 | 0,016807 |
2,09 | 3 | 0,069 | 0,207 | 0,014283 |
2,1 | 1 | 0,079 | 0,079 | 0,006241 |
Итого | 115 | 0,681 | 3,365 | 0,162435 |
Среднее значение отклонения можно оценить как
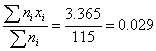
Среднее
квадратичное отклонение как
![]()
Необходимо
сформулировать две альтернативных гипотезы. Во-первых, можно предположить,
точность настройки не существенно различаются в зависимости от номинала. Эта
гипотеза называется нулевой гипотезой (H0). Альтернативная гипотеза
(H1), состоит в том, точность настройки различаются существенно в
зависимости от номинала.
Выпишем
несмещенные оценки генеральной дисперсии по формуле:
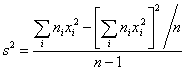
![]()
![]()
![]()
Для
проверки 0-гипотезы о равенстве генеральных дисперсий используется F-критерий
Фишера. На уровне значимости q 0-гипотеза имеет место, если отношение
выборочных дисперсий лежит в квантильных границах:
Чтобы
сравнить все 3 номинала, необходимо выполнить 3 оценки по критерию Фишера
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Выполнение
соотношения говорит о том, что можно принять 0-гипотезу. Если полученное на
практике отношение выборочных дисперсий выходит за левую границу этого
интервала, то нужно принять альтернативную гипотезу Sx<Sy.
А выход отношения выборочных дисперсий за правую границу − это область
альтернативной гипотезы Sx>Sy.
Теперь
вычисляются значение t-критерия и число степеней свободы n.
Сравнение
2.0 мм толщины и 1.9 мм толщины
Результат:
tЭмп = 1.6
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
2.08 | 2.83 |
Полученное эмпирическое значение t (1.6) находится в зоне незначимости.
Это означает, что при сравнении точности настройки номинала 2,0 мм и 1.9
мм точность настройки в зависимости от номинала отличается значительно.
Сравнение 2.0 мм толщины и 2.1 мм толщины.
Результат: tЭмп = 2.8
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.97 | 2.61 |
Полученное эмпирическое значение t (2.8) находится в зоне значимости.
Это означает, что при сравнении точности настройки номинала 2,0 мм и 2,1
мм точность настройки в зависимости от номинала отличается незначительно.
Сравнение 1,9 мм толщины и 2,1 мм толщины.
Результат: tЭмп = 1.3
Критические значения tКр | |
p ≤ 0.05 | p ≤ 0.01 |
1.98 | 2.63 |
Полученное эмпирическое значение t (1.3) находится в зоне незначимости.
Это означает, что при сравнении точности настройки номинала 1.9 мм и 2.1
мм точность настройки в зависимости от номинала отличается значительно.
.3 вычисление доли брака при различных настройках, которая
может быть использована как годная продукция другого сорта (номинала)
Для номинала 2 мм
Определяем долю годной продукции:
![]()
![]()
С
помощью таблицы функции нормального распределения получим
![]()
Доля
дефектной продукции
![]() , в
, в
процентах 2.78%
Из
них 2,02 % может быть пушена как годная продукция другого сорта.
Для
номинала 1,9 мм
Определяем
долю годной продукции:
![]()
![]()
С
помощью таблицы функции нормального распределения получим
![]()
Доля
дефектной продукции
![]() , в
, в
процентах 1.79%
Из
них 1,00 % может быть пушена как годная продукция другого сорта
Для
номинала 2,1 мм
Определяем
долю годной продукции:
![]()
![]()
С
помощью таблицы функции нормального распределения получим
![]()
Доля
дефектной продукции
![]() , в
, в
процентах 1.14%
Из
них 0,76 % может быть пушена как годная продукция другого сорта
4 Определение количества замеров толщины стенки листа стали
для уверенности в статистических выводах
Для того чтобы быть уверенным в статистических выводах, вероятность того,
что толщина листа попадает в интервал с заданными значениями должна быть не
меньше 95%. Отклонение величины от заданной вероятности должно быть не более
0,05.
Для 2 мм толщины:
мм-0,04<Толщина листа<2 мм 0,04
Для 1,9 мм толщины:
мм-0,05<Толщина листа<2 мм 0,05
Для 2,1 мм толщины:
мм-0,04<Толщина листа<2 мм 0,04
В предыдущем пункте мы уже определили, какова вероятность листов каждой
толщины считаются пригодными для использования:
Получились следующие данные:
мм: 97,22%
,9 мм 98,19%
,1 мм: 98,86%
Нужно,
чтобы условие ![]() выполнялось с вероятностью 0,95. Раскроем модуль и
выполнялось с вероятностью 0,95. Раскроем модуль и
найдем границы для m:
,65n<
m < 0,75n. По теореме Муавра – Лапласа:
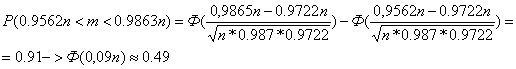
По
таблице находим
![]() n=129
n=129
Для
1,9 мм толщины:
Нужно,
чтобы условие ![]() выполнялось с вероятностью 0,95. Раскроем модуль и
выполнялось с вероятностью 0,95. Раскроем модуль и
найдем границы для m:
,9715n<
m < 0,9956n. По теореме Муавра – Лапласа:
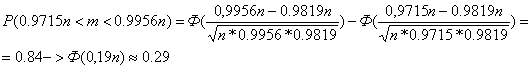
По
таблице находим
![]() n=65
n=65
Для
2,1 мм толщины:
Нужно,
чтобы условие ![]() выполнялось с вероятностью 0,95. Раскроем модуль и
выполнялось с вероятностью 0,95. Раскроем модуль и
найдем границы для m:
,9806n<
m < 0,9896n. По теореме Муавра – Лапласа:
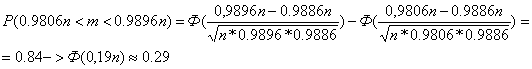
По
таблице находим
![]() n=27
n=27
Заключение
Проверка статистических гипотез – необходимая методика, используемая для
получения данных в статистике.
Проведенная работа позволила сделать следующие выводы:
· Под статистической гипотезой понимаются различного рода
предположения относительно характера или параметров распределения случайной
переменной, которые можно проверить, опираясь на результаты наблюдений в
случайной выборке.
· Смысл проверки статистической гипотезы состоит в том, чтобы
по имеющимся статистическим данным принять или отклонить статистическую
гипотезу с минимальным риском ошибки. Эта проверка осуществляется по
определенным правилам.
Анализируя результаты работы можно ответить на поставленный вопрос:
достаточно ли проводить только настройку технологического процесса или необходимо
уже проводить ремонт и замену оборудования для обеспечения заданной точности по
толщине металла.
Проведя все необходимые вычисления, мы пришли к выводу, что на данном
этапе достаточно проводить лишь настройку техпроцесса для каждого номинала.
Список литературы
статистический анализ технологический
1. Вентцель Е.С. Теория вероятностей. М., Высшая школа,
2002.
. Гмурман В.Е. Руководство к решению задач по теории
вероятностей и математической статистике. М., Высшая школа, 2004.
. Гмурман В.Е. Теория вероятностей и математическая
статистика. М., Высшая школа, 2003.
. Емельянов Г.В., Скитович В.П. Задачник по теории
вероятностей и математической статистике. М., Изд. МГУ, 1967.
. Коваленко И.Н., Филиппова А.А. Теория вероятностей и
математическая статистика. М, Высшая школа, 1982.
. Корн Г., Корн Т. Справочник по математике для
научных работников и инженеров. М., Наука, 1978.






