Вертикальная составляющая силы давления жидкости на криволинейные стенки.
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Определение силы давления жидкости на плоскую и криволинейную стенку. Суть гидростатического парадокса. Тело давления. Выделение на криволинейной стенке цилиндрической формы элементарной площадки. Суммирование горизонтальных и вертикальных составляющих.
презентация [1,8 M], добавлен 24.10.2021
Определение силы гидростатического давления жидкости на плоские и криволинейные поверхности, в закрытом резервуаре. Специфические черты гидравлического расчета трубопроводов. Определение необходимого давления рабочей жидкости в цилиндре и ее подачу.
контрольная работа [11,4 M], добавлен 26.10.2021
Гидростатическое давление и его свойства. Дифференциальное уравнение равновесия жидкости. Распределение гидростатического давления. Приборы для измерения давления. Сила гидростатического давления на плоские стенки и на криволинейную поверхность.
курс лекций [449,2 K], добавлен 20.12.2021
Виды вещества. Реакция твердого тела, газа и жидкости на действие сил. Силы, действующие в жидкостях. Основное уравнение гидростатики. Дифференциальное уравнение равновесия жидкости. Определение силы давления столба жидкости на плоскую поверхность.
презентация [352,9 K], добавлен 28.12.2021
Закон вязкого трения Ньютона. Определение равнодействующей силы гидростатического давления жидкости на плоские стенки. Понятие гидравлического радиуса. Геометрический и физический смысл понятий: геодезический, пьезометрический и гидравлический уклоны.
контрольная работа [150,1 K], добавлен 07.07.2021
Сила давления жидкости на криволинейную стенку.
Силы давления жидкости на поверхности произвольной формы в общем случае определяются, тремя составляющими суммарной силы и тремя моментами.
При действии жидкости на цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии, сила давления жидкости сводится к равнодействующей силе, лежащей в плоскости симметрии. Возьмем криволинейную поверхность АВ, образующая которой перпендикулярна к плоскости чертежа (рис.3.12а), определим силу давления жидкости на эту поверхность.
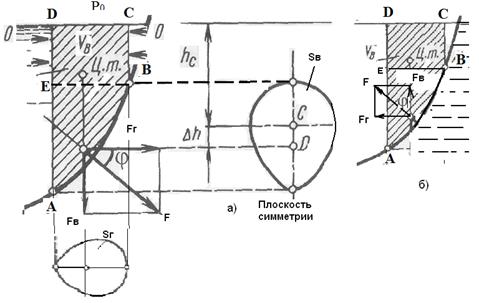
Рис.3.12. Определение сил давления на криволинейную стенку; а) жидкость внутри сосуда; б) жидкость вне сосуда.
Выделим объем жидкости, ограниченный поверхностью АВ, вертикальными плоскостями, проведенными через границы этого участка ВС и AD, свободной поверхностью жидкости. Рассмотрим условия равновесия объема АВСD в вертикальном и горизонтальном направлениях.
Сила давления жидкости F действует на стенку АВ, стенка АВ удерживает действие жидкости силой реакции стенки – R, направленной в противоположную сторону.
Условие равновесия объема АВСD в вертикальном направлении имеет вид
Fв= Р0Sг G = Р0Sг ρgVВ, (3.6)
где Р0 – давление на свободной поверхности жидкости; Sг – площадь горизонтальной проекции поверхности АВ; G – вес выделенного объема жидкостиV0, объем VВ называют объемом тела давления. Линия действия Fв проходит через ц.т. объема Vo.
Условие равновесия этого объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕD и BC взаимно уравновешиваются и остается лишь сила давления на площадь AЕ т. е. на вертикальную проекцию поверхности Sв. Тогда
Fг= Sвρghc Sв Р0 = Sв(ρghc Р0). (3.7)
Направление горзонтальной силы находится по правилам , соответствующим силе, действующей на плоскую стенку.
Определив по формулам (3.7) и (3.6) вертикальную и горизонтальную составляющие полной силы Рж, найдем
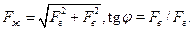 (3.8)
(3.8)
Сила давления жидкости на криволинейную стенку будет равна силе реакции стенки Rж = P и направлена в противоположную сторону.
Когда жидкость расположена снаружи (рис.3.12б), сила гидростатического давления на криволинейную поверхность АВ определяется также, но направление ее будет противоположным.
В условия равновесия, как и в первом случае, входит вес жидкости G в объеме АВСD, хотя этот объем и не заполнен жидкостью.
Положение центра давления на цилиндрической стенке можно найти, если известны площади Sв и Sг и определен центр тяжести выделенного объема АВСD.
Для стенок постоянной кривизны (цилиндрических, сферических) полная сила давления проходит через центр или ось кривизны стенки.
При избыточном давлении на смоченной стороне стенки все составляющие и полная сила давления жидкости направлены от жидкости на стенку (изнутри наружу), рис.3.13а.
В случае разрежения на смоченной стороне стенки силы направлены снаружи внутрь сосуда, рис.3.13б.
При двустороннем воздействии жидкостей на стенку сначала определяются горизонтальные и вертикальные составляющие с каждой стороны стенки в предположении одностороннего воздействия жидкости, а затем суммарные горизонтальная и вертикальная составляющие от воздействия обеих жидкостей.
На рис. 3.13 показано определение горизонтальной и вертикальной составляющих и полной силы давления жидкости на симметричную стенку АВ при избыточном давлении (а) и при разрежении (б) на смоченной стороне стенки.
Объем, построенный на криволинейной поверхности, ограниченный цилиндрической вертикальной поверхностью и сверху пьезометрической плоскостью называется объемом тела давления.
Тело давления в обоих случаях ограничено пьезометрической плоскостью, сила давления в случае избыточного давления направлена наружу, в случае разряжения внутрь сосуда. В ряде задач силу давления на криволинейную стенку удобнее находить по ее составляющим вдоль наклонных осей.
Сила давления жидкости на стенку по любому заданному направлению s (рис. 3.14)
Ps= GsCosα = ρgVsCosα, (3.9)
где Gs – вес жидкости в объеме Vs, ограниченном стенкой, пьезометрической плоскостью и проектирующей поверхностью, параллельной заданному направлению; α – угол между заданным направлением и вертикалью.

Рис.3.13. Силы давления на криволинейную стенку при действии: а) избыточном давлении в сосуде; б) при вакууме.
Линия действия силы Рs проходит через центр тяжести жидкости в объеме Vs.
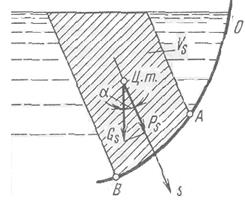
Рис.3.14 Определение силы давления жидкости по заданному направлению.
В некоторых случаях для нахождения той или иной составляющей силы давления жидкости на стенку следует разбить ее поверхность на отдельные участки, определить соответствующие усилия на каждый участок стенки и далее просуммировать их.
Для определения вертикальной составляющей силы давления жидкости на полусферическую стенку abc следует разделить поверхность полусферы горизонтальной плоскостью на верхнюю ab и нижнюю bc половины и найти вертикальные силы давления жидкости на каждую из них (рис. 3.15).
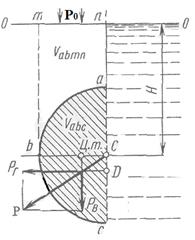
Рис.3.15 Определение силы давления жидкости на полусферическую стенку разбиением на два объема.
Вертикальная сила на стенку ab равна весу жидкости в объеме аbтп (Рab= ρgVabmn) и направлена вверх; вертикальная сила на стенку bс равна весу жидкости в объеме сbтп (Рbc= ρgVсbтп) и направлена вниз. Следовательно, вертикальная сила давления на всю полусферу аbс равна разности указанных сил:
Pв = Pbc – Pab = ρg(Vbcmn – Vabmn) = ρgVabc,
т.е. равна весу жидкости в объеме полусферы и направлена вниз.
Возможным приемом расчета силы давления является рассмотрение равновесия объема жидкости, заключенного между стенкой и плоским сечением, проведенным через ее граничный контур. Например, требуется определить силу Р давления жидкости на коническую крышку (рис. 3.16).
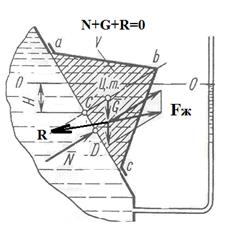
Ри.3.16. Определение силы давления жидкости при рассмотрении
равновесия объема жидкости в крышке.
Условие равновесия объема жидкости, заполняющей конус, выражается векторным уравнением
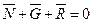 ,
,
где N – сила давления жидкости на выделенный объем, т.е. на плоское сечение ас (N=ρgHFac ) и проходит по нормали к сечению через центр давления D); G – вес выделенного объема жидкости (G = ρgV); R – сила действия конуса на жидкость. Так как искомая сила Fж равна и противоположна силе R, получаем уравнение
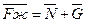 ,(3.10)
,(3.10)
из которого можно определить силу давления Р или любую ее составляющую.
Плавание тел.
Выталкивающая сила является равнодействующей сил давления, с которыми жидкость, находящаяся в покое, действует на тело.
В жидкость погружено тело произвольной формы объемом Wт (рис.3.17). 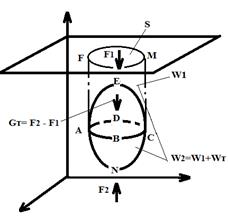
Рис.3.17 Выталкивающая сила
На свободную поверхность жидкости тело проектируется в виде сечения S, по этой поверхности проведем цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой АВСD. Эта кривая отделяет верхнюю часть поверхности тела от нижней ее части.
Вертикальная составляющая силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме АFCME.
F1 = ρgW1
Вертикальная составляющая силы давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме ANCMF.
F2 = ρgW2.
Разность между этими силами равна вертикальной равнодействующей сил давления жидкости на тело, будет направлена вверх и равна весу жидкости в объеме жидкости, вытесненной телом.
Gж = F2 – F1 = ρg(W2-W1)= ρgWт=FA. (3.11)
Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила направленная вертикально вверх, равная весу жидкости вытесненной телом и приложенная в центре тяжести объема погруженной части тела.
Центр тяжести объема погруженной части тела называется центром водоизмещения или центром давления, так как в этой точке приложена равнодействующая сил давления на тело.
Объем жидкости, вытесненный телом, называется объемным водоизмещением.
Выталкивающая сила называется также силой Архимеда.
Вес G тела и архимедова сила могут находиться в следующих соотношениях:
1) G > FА – отрицательная плавучесть, тело тонет;
2) G < FА – положительная плавучесть, тело всплывает и плавает на поверхности жидкости;
3) G = FА нулевая плавучесть, погруженное в жидкость тело плавает.
Линия пересечения свободной поверхности с поверхностью плавающего тела называется ватерлинией.
Для равновесия плавающего тела, кроме равенства G = FА должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения.
Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии, заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:







