Тема №4. оценка достоверности результатов исследования
ЦЕЛЬ ЗАНЯТИЯ. Освоить параметрические методы оценки достоверности результатов статистического исследования и овладеть методикой расчета ошибок средних и относительных величин, доверительных границ этих величин, методикой расчета достоверности разности средних и относительных величин.
МЕТОДИКА ПРОВЕДЕНИЯ ЗАНЯТИЯ. Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют ошибки репрезентативности средних и относительных показателей, доверительные границы выборочных производных величин, оценивают достоверность разности между сравниваемыми выборочными величинами. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Что оказывает влияние на достоверность статистических данных?
2. Какая доверительная вероятность допустима в медицинских исследованиях?
3. Какой будет величина коэффициента достоверности при вероятности безошибочного прогноза 95%?
4. Какая формула используется для определения ошибки относительного показателя?
5. Какая формула применяется для оценки достоверности различий между относительными величинами?
6. Как оценить критерий достоверности при больших и малых выборках?
КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:
При вычислении показателей довольно часто используют не всю генеральную совокупность, а только какую-то часть ее (например, при выборочном исследовании). Для того, чтобы по части явления можно было судить о явлении в целом, о его закономерностях, необходима оценка достоверности результатов исследования. Мерой достоверности показателя является его ошибка – ошибка представительности (репрезентативности). Ошибка показывает, насколько результат, полученный при выборочном исследовании, отличается от результата, который мог бы быть получен при сплошном исследовании всей генеральной совокупности. Средняя ошибка средней арифметической (m) равняется отношению среднеквадратического отклонения к квадратному корню из числа наблюдений. Средняя ошибка относительных показателей рассчитывается по формуле: m =  , где р – соответствует величине относительного показателя, q =100 – p, если относительный показатель выражен в процентах, 1000 – р, если показатель вычислен в промилле и т.д. С увеличением числа наблюдений достоверность выборочного результата увеличивается, но это не значит, что следует стремиться бесконечно увеличивать число наблюдений. Это не нужно, а иногда и практически неосуществимо. Относительно небольшой, но качественно однородный статистический материал дает достаточно надежные выводы.
, где р – соответствует величине относительного показателя, q =100 – p, если относительный показатель выражен в процентах, 1000 – р, если показатель вычислен в промилле и т.д. С увеличением числа наблюдений достоверность выборочного результата увеличивается, но это не значит, что следует стремиться бесконечно увеличивать число наблюдений. Это не нужно, а иногда и практически неосуществимо. Относительно небольшой, но качественно однородный статистический материал дает достаточно надежные выводы.
В тех случаях, когда уровень относительного показателя превышает величину основания (общий уровень заболеваемости составил 1300 случаев на 1000 человек), определение ошибки представительности по указанной выше формуле становится невозможным, и если показатель находится в пределах от 1,0 до 1,5 в среднем на одного человека, то ошибку представительности следует определять по формуле: m =  , где М – среднее число заболеваний на одного человека (при заболеваемости 1300‰ – М = 1,3), n –общее число наблюдений.
, где М – среднее число заболеваний на одного человека (при заболеваемости 1300‰ – М = 1,3), n –общее число наблюдений.
Оценить достоверность результатов исследования — значит, установить вероятность прогноза, с которой результаты исследования на основе выборочной совокупности можно перенести на генеральную совокупность или другие исследования. Ошибка представительности (репрезентативности) позволяет определить пределы, в которых с соответствующей степенью вероятности безошибочного прогноза находится истинное значение искомого параметра, т.е. доверительные границы. Pген = Pвыб ± tm (для относительных показателей), Мген = Мвыб ± tm (для средних величин), где Рген и Мген – искомые генеральные параметры частоты и среднего уровня, Рвыб и Мвыб – найденные выборочные показатели, m – ошибка представительности, t – доверительный критерий. Определенной степени вероятности безошибочного прогноза соответствует константное значение доверительного критерия, величина которого определяется по таблице интеграла вероятностей (при n>30, приложение, табл. 1) или по таблице критерия t (при n<30, приложение, табл. 2). При использовании таблицы критерия t число степеней свободы для доверительных границ составляет n -1. В медико-социальных исследованиях минимальной достаточной вероятностью безошибочного прогноза является 95% (Pt =0,95), что допускает вероятность ошибки р = 0,05. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы, вероятность безошибочного прогноза возрастает до 99% (Pt =0,99, или р = 0,01) и даже до 99,9% (Pt =0,999, р = 0,001). Доверительные границы используются не только для оценки достоверности выборочного результата, но и при планировании в здравоохранении.
В качестве примера расчета доверительных границ средних показателей рассмотрим изменения среднего роста девочек 3-х лет. В результате проведенного исследования было установлено, что при n = 34 средний рост характеризуется: M = 101.6 см, 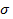 = 15.0 см.
= 15.0 см.
Подставляем известные значения в формулу:
m =  см, Мген = Мвыб ± tm = 101,6 ±2×2,57 см
см, Мген = Мвыб ± tm = 101,6 ±2×2,57 см
В результате проведённых вычислений мы, конечно, не узнали “истинное” значение среднего роста 3-х летних девочек в рассматриваемой популяции, однако теперь с 95 % вероятностью можно утверждать, что он находится в пределах 101.6 ± 2×2,57 см, то есть от 96.5 до 106.7 см.
Вычисленные таким способом доверительные интервалы будут эффективно отражать анализируемое явление, когда распределение исходных вариантов соответствует нормальному. Величина t показывает, во сколько раз необходимо увеличить стандартную ошибку выборочного статистического параметра для того, что бы при определенном уровне вероятности судить о тех пределах, в которых располагается генеральное значение. Использование этой таблицы не требует особых вычислений, поскольку величина t напрямую зависит лишь от уровня вероятности P и числа степеней свободы n’. В большинстве биологических исследований принимают P=0.95 (то есть 95 случаев из 100), в наиболее ответственных случаях – 0.99 или 0.999. Число степеней свободы n’ при нахождении доверительных интервалов для M равно: n’ = n – 1.
Наиболее распространенным методом оценки достоверности разности между сравниваемыми выборочными результатами является критерий Стьюдента, предложенный В. Госсетом. Критерий t позволяет производить сравнение только между двумя выборочными величинами. Если необходимо сравнить между собой несколько однородных выборочных величин, то они сравниваются поочередно. Критерий достоверности (Стьюдента) определяется как величина разности средних величин или относительных показателей, деленная на извлеченную из квадратного корня сумму квадратов ошибок средних арифметических или относительных показателей.
t =  t =
t = 
Разница между сравниваемыми выборочными величинами существенна и статистически достоверна при вероятности безошибочного прогноза 95%, т.е. величина критерия Стьюдента должна быть равна или больше 2 (при n >30). Только при этих условиях прогноз считается безошибочным, свидетельствующим о надежности используемого нового метода (лекарственного препарата, гигиенических характеристик).
Например, в процессе специальных исследований было установлено, что у стариков до лечения инсулином среднее содержание белков в крови составляло 81,04 ± 1.7, а после лечения – 79,33±1.6. Нетрудно видеть, что полученные величины неодинаковы. Но достоверно ли это различие, закономерно ли оно? Можно ли на его основании утверждать, что лечение инсулином понижает содержание белков в крови? Ответ на этот вопрос может дать критерий достоверности различий средних арифметических.  = 0.7.
= 0.7.
Поскольку полученное значение (0.7) меньше двух, различия между средними величинами статистически недостоверны (незначимы). Следовательно, влияние инсулина на содержание белков в крови приведенными выше данными не подтверждается и остается недоказанным, возможно, из-за недостаточного числа определений.
Приведем другой пример: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 час после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту. Нужно оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 часа работы.

Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99%, следовательно, можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч. работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
Для малых по объему выборок лучшим способом определения достоверности различий разнообразия признаков является критерий F Фишера.
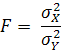
где 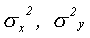 – дисперсии первой и второй выборки соответственно. Как уже было отмечено, показателем степени разнообразия служит основное отклонение — σ (сигма). Еще более чувствительным показателем степени разнообразия (варьирования, дисперсии, разброса данных) служит σ2(варианса, девиата, дисперсия).
– дисперсии первой и второй выборки соответственно. Как уже было отмечено, показателем степени разнообразия служит основное отклонение — σ (сигма). Еще более чувствительным показателем степени разнообразия (варьирования, дисперсии, разброса данных) служит σ2(варианса, девиата, дисперсия).
Так как, согласно условию вычисления критерия, величина числителя должна быть больше или равна величине знаменателя, то значение F всегда будет больше или равно единице. Число степеней свободы определяется также просто:
k1=n1– 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k2=n2 – 1 для второй выборки.
В приложении, табл. 5 критические значения критерия Фишера находятся по величинам k1 (верхняя строчка таблицы) и k2 (левый столбец таблицы). Если tэмп>tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная.
Пример.В двух третьих классах проводилось тестирование умственного развития десяти учащихся. Полученные значения средних величин достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами.
Решение. Для критерия Фишера необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
| №№ учащихся | Первый класс | d | d2 | Второй класс | d | d2 |
| 29,4 | 864,4 | -22,6 | 510,8 | |||
| -31,6 | 998,6 | -14,6 | 213,2 | |||
| -21,6 | 466,6 | -7,6 | 57,8 | |||
| 18,4 | 338,6 | 0,4 | 0,16 | |||
| 27,4 | 750,8 | 8,4 | 70,6 | |||
| -7,6 | 57,8 | 1,4 | 1,96 | |||
| -26,6 | 707,6 | -0,6 | 0,36 | |||
| -20,6 | 424,4 | 23,4 | 547,6 | |||
| 14,4 | 207,4 | 13,4 | 179,6 | |||
| 18,4 | 338,6 | -1,6 | 2,6 | |||
| Суммы | 5154,8 | 1584,7 | ||||
| Среднее | 60,6 | 63,6 |
Среднеквадратическое отклонение для простого ряда при числе наблюдений меньше 30 вычисляется по формуле:

Дисперсия представляет собой сумму средних квадратов отклонений. Рассчитав дисперсии для переменных X и Y, получаем:
sx2=572,83; sy2=176,07
Тогда по формуле для расчета по критерию Фишера F находим
F = 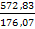 =3,25
=3,25
В приложении по таблице 5 находим критическое значение(достоверное)для F критерия при степенях свободы, в обоих случаях равных k=10 – 1 = 9, находим Fкрит=3,18 (<3.25), следовательно, можно утверждать, что Н0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н1. Исследователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
ЗАДАНИЕ №1. Определить доверительные границы с вероятностью безошибочного прогноза 99% для относительных показателей, вычисленных из следующих задач:
Задача 1
Анкетирование подростков показало, что из 168 опрошенных школьников оценивают свое состояние здоровья как хорошее 95 человек. Вычислите экстенсивный показатель и определите его доверительные границы.
Задача 2
Среди 328 опрошенных медицинских работников 110 считают, что лекарственное обеспечение медицинских учреждений за последние десять лет ухудшилось. Вычислите экстенсивный показатель и определите его доверительные границы.
Задача 3
При обследовании 256 больных гипертонической болезнью у 49 были обнаружены заболевания почек. Вычислите распространенность почечной патологии у больных гипертонической болезнью и определите её доверительные границы.
Задача 4
Анализ выборочного опроса 145 студентов первого курса медицинского университета показал, что профессиональный выбор определялся личной заинтересованностью у 115 человек, тогда как 30 человек поступили в вуз, следуя желанию родителей. Вычислите один из экстенсивных показателей и определите его доверительные границы.
Задача 5
316 пациентам, больным гриппом было проведено электрокардиографическое исследование. Изменения со стороны сердечно-сосудистой системы выявлены у 72 человек. Вычислите частоту изменений со стороны сердца при гриппе – интенсивный показатель и определите его доверительные границы.
Задача 6.
Из 196 больных, перенесших инфаркт миокарда, у 41 через год возник повторный инфаркт. Вычислите частоту рецидивов после перенесенного инфаркта миокарда и доверительные границы интенсивного показателя.
Задача 7
У 305 из 950 обследованных на медицинской комиссии в военкомате призывников были обнаружены заболевания, ограничивающие годность к военной службе. Вычислите уровень заболеваемости призывников и доверительные границы интенсивного показателя.
Задача 8
Из 180 больных, перенесших инсульт, трудоспособность полностью восстановилась у 47 человек. Вычислите показатель частоты восстановления трудоспособности и доверительные границы интенсивного показателя.
Задача 9
При медицинском осмотре было установлено, что из 260 рабочих, нарушавших режим питания, желудочно-кишечными заболеваниями страдают 98 человек. Вычислите уровень заболеваемости рабочих и доверительные границы интенсивного показателя.
Задача 10
По окончании начальной школы у 440 детей из 1120 обучающихся была выявлена миопия. Вычислите частоту возникновения миопии у школьников начальных классов и доверительные границы интенсивного показателя.
Задача 11
При флюорографическом обследовании 250 заключенных патологические изменения в легких были выявлены у 88 человек. Вычислите показатель частоты патологических изменений выявленных при флюорографическом обследовании и доверительные границы интенсивного показателя.
Задача 12
В участковой больнице села Заветного имеется 35 коек, средняя численность обслуживаемого населения составила 5890 человек. Вычислите обеспеченность сельского населения стационарной помощью и доверительные границы показателя соотношения.
Задача 13
Из 45 иностранных студентов – выпускников СтГМУ в 2021 году диплом с отличием получили пятеро. Вычислите удельный вес отличников и доверительные границы экстенсивного показателя.
Задача 14
При изучении частоты заболеваемости дошкольников ОРВИ было установлено, что на 420 детей приходится 310 зарегистрированных случаев заболеваний ОРВИ. Вычислите частоту заболеваемости ОРВИ у дошкольников и доверительные границы интенсивного показателя.
ЗАДАНИЕ №2. Оцените достоверность разности средних и относительных показателей
Задача 1
У студентов-медиков исследовали уровень максимального артериального давления до и после сдачи экзамена по фармакологии. Оказалось, что до сдачи экзамена уровень максимального артериального давления в среднем составил 130,5±5,0 мм рт. ст., а после сдачи 118,4±4,1 мм рт. ст. Достоверно ли повышение давления у студентов перед сдачей экзамена?
Задача 2
Результаты проведенного опроса в России и Финляндии показали, что активно пробовали наркотики 45,9±3,2% российских подростков из семей служащих, тогда как в Финляндии этот показатель составил 38,5±4,7%. Можно ли утверждать, что подростки РФ достоверно чаще приобщаются к наркотикам?
Задача 3
Доля женщин 15-49 лет, имевших хотя бы один аборт в анамнезе, в Ставропольском крае составила 52,6±2,6, в Ингушетии 44,3±1,8. Можно ли утверждать, что ставропольские женщины достоверно чаще прибегают к абортам, чем в Ингушетии.
Задача 4
Оценить достоверность различий между показателями заболеваемости с временной утратой трудоспособности рабочих основных профессий (183,7±2,3%) и показателями заболеваемости инженерно-технических работников (143,1±3,3%).
Задача 5
Оценить достоверность различий между распространенностью симптомов аллергического ринита у детей младшего школьного возраста – 9,7±1.2% и старшего школьного возраста – 14,5±1,4%. Можно ли утверждать, что эти показатели существенно отличаются?
Задача 6
Оценить достоверность различий между среднегодовой занятостью койки в городской детской больнице – 264,2±6,2 и в краевой детской больнице – 322,8±4,4. Можно ли утверждать, что эти показатели существенно отличаются?
Задача 7
Оценить достоверность различий средней длительности пребывания больных с холециститами в стационаре при применении эндоскопического метода хирургического лечения (11,3±0,9 дня) и лапаротомического метода оперативного лечения (20,5±1,2 дня). Можно ли утверждать, что эти показатели существенно отличаются?
Задача 8
Средняя стоимость одного посещения поликлиники по заболеванию мочевой системы в 2021году составила 174,3±3,2 рубля, а в 2021 году 198,8±1,7 рубля. Можно ли утверждать, что средняя стоимость одного посещения поликлиники по поводу заболевания мочевой системы достоверно возросла?
Задача 9
Оценить достоверность влияния радоновых ванн и физических тренировок на экстрасистолию больных ишемической болезнью сердца, если среднее число желудочковых экстасистол, по данным амбулаторного мониторирования за 24 часа, составило до лечения 1443±99, а после лечения 356±58.
Задача 10
Оценить достоверность влияния комплекса лечебных факторов курорта на жирно-кислотный спектр сыворотки крови у больных псориазом, если сумма ненасыщенных жирных кислот в сыворотке крови в среднем составила до лечения 65,58±1,36 , а после лечения 66,28±1,81 мкг/мл.
Задача 11
Количество диагностических исследований, выполненных в среднем на одного больного в дневных стационарах Ставрополя, составило в 2021 году 5,2±0,5, а в 2021 году 6,5±0,7. Можно ли утверждать, что полнота обследования больных в дневных стационарах достоверно увеличивается?
Задача 12
Лечение компенсированного хронического тонзиллита препаратом «Тонзинал» в условиях стационара дневного пребывания показало повышение уровня иммуноглобулинов сыворотки крови, так уровень иммуноглобулина G до лечения составлял в среднем 141,2±11,3, а после четырехдневного лечения 162,3±9,8. Можно ли утверждать, что уровень общего иммунитета после проведенного курса лечения хронического тонзиллита препаратом Тонзинал достоверно повышается?
Задача 13
Оцените достоверность различий между частотой вызовов скорой помощи больными ИБС в зимне-весенние месяцы (в декабре – мае показатель обращаемости составил 283,2±14,1‰) и в летне-осенние месяцы, когда уровень обращаемости составил 198,4±10,8‰.
Задача 14
Оцените достоверность различий веса новорожденных, если средний вес родившихся у первородящих матерей составил 3,350±0,2 кг, а у повторнородящих 3,72±0,3 кг. Можно ли утверждать, что эти показатели существенно отличаются?
Задание №3. Вычислите относительные показатели, ошибки относительных показателей и определите достоверность разности относительных показателей
Задача 1
Из 260 детей 8-летнего возраста, игравших в компьютерные игры длительнее 3 часов в день, нарушение остроты зрения отмечено у 61 ребенка, а из 140 детей этого же возраста, игравших в компьютерные игры менее 2 часов, у 22 детей. Достоверно ли снижение остроты зрения у детей при длительной работе на компьютере?
Задача 2
В абдоминальное отделение краевого онкологического диспансера за квартал госпитализировано 158 больных раком ободочной кишки, в том числе в возрасте до 60 лет – 70 человек, старше 60 лет – 88. Радикальные операции выполнены 102 больным, в том числе 54 пациентам в возрасте до 60 лет и 48 – пациентам пожилого и старческого возраста. Определите, имеется ли достоверное снижение операбельности у больных пожилого и старческого возраста.
Задача 3
На базе Ставропольского краевого родильного дома изучались распространенность и последствия хламидийной инфекции у беременных женщин. Из 516 беременных женщин наличие хламидийной инфекции выявлено у 165. Угроза прерывания беременности наблюдалась у 75 женщин, не имевших хламидийной инфекции, и у 72, страдавших этим заболеванием. Повышается ли угроза прерывания беременности при наличии хламидийной инфекции?
Задача 4
В центре сосудистой хирургии краевой клинической больницы консервативное лечение трофических язв нижних конечностей проводилось у 35 больных, из которых у 12 отмечено рубцевание язвы. Оперативное лечение проведено 44 больным, для чего был использован метод облитерации задних большеберцовых вен по А.Н. Веденскому. К моменту выписки из стационара у 26 прооперированных пациентов язвы полностью зажили. Эффективен ли оперативный метод при лечении трофических язв нижних конечностей?
Задача 5
Изучение обращаемости 30-40-летних мужчин за медицинской помощью показало, что из 230 человек, злоупотребляющих алкоголем, в медицинские учреждения обратилось 27 человек, а из 488 мужчин, не имеющих этой вредной привычки, за медицинской помощью обратились 50 человек. Имеется ли достоверная разница в частоте обращаемости за медицинской помощью 30-40-летних мужчин, злоупотребляющих алкоголем и не имеющих этой привычки?
Задача 6
При анализе производственного травматизма у сельского населения было установлено, что на 1450 работающих в сельском хозяйстве приходится 63 случая травм, в том числе 44 случая травм – у мужчин (830 человек) и 19 – у женщин. Имеются ли достоверные отличия уровней травматизма у мужчин и женщин?
Задача 7
Результаты лечения больных детским церебральным параличом с использованием корригирующего костюма (костюма космонавта) показали, что из 48 больных гиперкинетической формой положительная динамика неврологического статуса наблюдалась у 40 детей, а из 13 больных с гемипаретической формой – у 4. Имеется ли достоверная разница эффективности лечения при различных клинических формах ДЦП?
Задача 8
Оцените эффективность лечебно-профилактической работы в санаторной школе-интернате, если из 250 учащихся при поступлении к группе риска (часто и длительно болеющих острыми заболеваниями) были отнесены 165 человек, а по окончании учебного года к этой группе уже относилось 133 человека, тогда как 32 ребенка перешли в группу практически здоровых. Имеется ли достоверная разница в здоровье детей до и после лечения в школе-интернате?
Задача 9
Изучалась распространенность употребления алкоголя в студенческой среде. Анонимному анкетированию были подвергнуты 1458 студентов 1-3 курсов и 1090 студентов 4-6 курсов. Установлено, что употребляют алкоголь не реже одного раза в неделю на младших курсах 630 студентов, а на старших – 588 студентов. Существует ли достоверная разница между частотой употребления алкоголя на разных этапах обучения?
Задача 10
Изучалась суточная летальность при мозговых инсультах. Проанализированы истории болезни 98 жителей г. Пятигорска, умерших от мозговых инсультов, причем во временной промежуток с 2100 до 5 часов утра умерло 44 человека, во вторую треть суток с 1300 до 2100 – 31 человек, а в первую часть суток с 500 до 1300 – 23 человека. Имеется ли достоверная разница в колебаниях летальности от мозговых инсультов в зависимости от суточных биоритмов?
Задача 11
Из 360 больных, направленных в стационар станцией скорой и неотложной помощи, случаи расхождения диагнозов были отмечены у 42 пациентов, а из 113 больных, направленных поликлиникой, случаи расхождения диагнозов между поликлиникой и стационаром отмечены у 10 пациентов. Имеется ли достоверная разница в качестве диагностики в поликлинике и станции скорой и неотложной помощи?
Задача 12
Из 63 пациентов хирургического отделения, прооперированных с помощью плазменного скальпеля, гладкое послеоперационное течение отмечено у 59 человек, тогда как из 42 больных, прооперированных обычным способом, послеоперационных осложнений не было у 26 человек. Действительно ли применение плазменного скальпеля достоверно улучшает результаты лечения?
Задача 13
При выяснении уровеня компьютерной грамотности врачей и сестер-руководителей, получены следующие результаты: из 77 опрошенных врачей владеют компьютером в объеме пользователя 50 человек, а из 29 опрошенных старших медицинских сестер – 12. Имеется ли достоверная разница в уровне компьютерной грамотности врачей и старших медицинских сестер?
Задача 14
Проведено исследование психоэмоционального состояния у 457 работающих на оборонном предприятии мужчин. Среди обследованных рабочих – 172 человека курили, а 285 этой вредной привычки не имели. Повышенный уровень психоэмоционального напряжения отмечен у 79 курящих рабочих и у 94 не курящих. Достоверно ли отличается уровень психоэмоционального напряжения у курящих рабочих?
Задание №4. Вычислите ошибки средних величин и оцените достоверность разности двух средних показателей
Задача 1
Средний возраст вступления в брак у 350 опрошенных студенток составил 19,8 года, среднеквадратическое отклонение равно 11,4, тогда как аналогичный показатель у 265 студентов-мужчин оказался равным 21,5 года, а среднеквадратическое отклонение составило 8,6. Достоверно ли отличается средний возраст вступления в брак у студентов разного пола?
Задача 2
Средний уровень гемоглобина у 445 детей, получавших коровье молоко с первых месяцев жизни (до 3-х месяцев), составил 114,69 (среднеквадратическое отклонение равно 5,8). У 326 детей, получавших коровье молоко начиная с 7 месяца жизни, средний уровень гемоглобина составил 117,5, а среднеквадратическое отклонение 4,5. Достоверно ли отличается средний уровень гемоглобина у детей с разными сроками введения коровьего молока в рацион?
Задача 3
Средняя продолжительность одного случая временной нетрудоспособности у студентов 1 курса лечебного факультета (всего 41 случай ВН) составила 5,8 дня, среднеквадратической отклонение равно 2,3, тогда как у студентов стоматологического факультета средняя продолжительность одного случая временной нетрудоспособности (всего 35 случаев ВН) составила 3,6 дня, а среднеквадратическое отклонение 1,9. Достоверно ли отличается средняя продолжительность одного случая временной нетрудоспособности на двух факультетах?
Задача 4
Средний уровень успеваемости 315 студентов 6 курса лечебного факультета по дисциплине «Общественное здоровье и здравоохранение» составил 4,3 балла, среднеквадратическое отклонение равно 1,6, тогда как у 119 студентов педиатрического факультета эти показатели соответственно равны 3,9 балла и 1,1. Достоверно ли отличается уровень успеваемости выпускников на двух факультетах?
Задача 5
Среднее число беременностей у 210 женщин 35 лет, имевших самопроизвольные аборты в анамнезе, составило 6,3, при этом среднеквадратическое отклонение равно 2,8, а у 432 женщин этого же возраста, не имевших самопроизвольных абортов, среднее число беременностей составило 2,9, а среднеквадратическое отклонение равно 5,4. Достоверно ли отличается число беременностей у женщин, имевших самопроизвольные аборты в анамнезе?
Задача 6
Средний срок наблюдения за 189 пациентами с неосложненной формой острого аппендицита в стационаре составил 8,2 дня, при среднеквадратическом отклонении равном 3,1, тогда как при осложненной форме (53 чел.) длительность пребывания в стационаре увеличилась у до 11,4 дня при среднеквадратическом отклонении равном 2,2. Достоверно ли увеличивается средний срок пребывания в стационаре при осложненной форме острого аппендицита?
Задача 7
Средний рост мальчиков 7 лет в 389 семьях со здоровым образом жизни составил 130,5 см. (σ =4,3), а в 59 неблагополучных по алкоголизму семьях 123,3 см. (σ =5,8). Достоверно ли снижение роста у детей в семьях неблагополучных по алкоголизму?
Задача 8
Средний возраст первого сексуального опыта у 266 опрошенных городских девушек составил 15,2 года, при среднеквадратическом отклонении равном 4,8; тогда как у 150 сельских девушек он составил 16,9 года, при среднеквадратическом отклонении равном 7,6. Имеется ли статистически достоверная разница между началом половой жизни у городских и сельских девушек?
Рекомендуемая литература:
· Медик В.А., Юрьев В.К.Общественное здоровье и здравоохранение. Учебник для вузов: – М: ГЭОТАР – Медиа. – 2021, – 608 с.
· Медик В.А.Общественное здоровье и здравоохранение: Руководство к практическим занятиям: – М: ГЭОТАР – Медиа. – 2021, – 400 с.
· Щепин О.П., Медик В.А.Общественное здоровье и здравоохранение. Учебник для вузов: – М., 2021, – 592 с.
· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
· Серенко А.Ф., Ермаков В.В. Социальная гигиена и организация здравоохранения, М, 1984, с.139 – 149.
· Юрьев В.К., Куценко Г.И. Общественное здоровье и здравоохранение. С-П, 2000, с. 197 – 199.
· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова М. «МЕДпресс-информ»., 2002. – с. 108-109, 113-114.
§
ЦЕЛЬ ЗАНЯТИЯ: Освоить методику вычисления и использования критерия соответствия для определения достоверности расхождения между несколькими сравниваемыми группами изучаемых явлений.
Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют критерий соответствия для определения достоверности расхождения между несколькими сравниваемыми группами изучаемых явлений, оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
- Когда применяется показатель соответствия «хи-квадрат»?
- На чем основан расчет показателя χ2?
- Что такое «нулевая гипотеза»?
- Из каких этапов складывается исчисление критерия соответствия «хи-квадрат»?
- Как определяется число степеней свободы при расчете критерия соответствия?
- Как оценивается полученный результат показателя соответствия?
- Когда различия между несколькими сравниваемыми группами оцениваются как существенные?
КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:
Непараметрическими являются количественные методы статистической обработки данных, применение которых не требует знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Описанные выше статистические критерии достоверности (критерий Стьюдента t, критерий Фишера F и др.) относятся к параметрическим, т. к. используют стандартные параметры распределений (М, Р, m, n). Они связаны с законом нормального распределения и применяются для оценки расхождения между генеральными параметрами по выборочным показателям сравниваемых совокупностей. Существенным достоинством параметрических критериев служит их большая статистическая мощность, т. е. широкие разрешающие возможности, а недостатком – трудоемкость расчетов, неприменимость к распределениям, сильно отклоняющимся от нормального, а также при исследовании качественных признаков.
Наряду с параметрическими критериями для ориентировочной оценки расхождений между выборками (особенно небольшими) применяются так называемые непараметрические критерии, что позволяет сравнивать выборки как по количественным, так и по качественным признакам, значения которых не имеют числового представления, но которые можно ранжировать. Конструкции непараметрических критериев отличаются простотой.
В медицине для доказательства некоторого утверждения часто применяют метод, известный в математике как «доказательство от противного». Для этого в качестве рабочего инструмента используют так называемую «нулевую гипотезу». Гипотеза, в соответствии с которой отсутствуют различия между различными совокупностями, называется нулевой гипотезой.
Например, если надо показать, что заболеваемость в целом ниже у лиц, занимающихся физкультурой и спортом, чем у ведущих малоподвижный образ жизни, то выдвинем гипотезу об отсутствии различий в их состоянии здоровья. Затем попробуем отвергнуть эту гипотезу.
«Нулевая гипотеза» широко используется при оценке достоверности различия сравниваемых групп по критерию соответствия (хи-квадрат).
Критерий соответствия χ2 применяется для статистической оценки закона распределения эмпирических вариационных рядов и для доказательства достоверности различий между двумя или несколькими выборочными совокупностями. Критерий соответствия применяется, когда результаты исследования представлены абсолютными величинами, и результат исхода имеет много градаций (выздоровел, состояние улучшилось, ухудшилось, умер), а также, если в подлежащем имеется несколько признаков (несколько возрастных групп, несколько методов лечения, кормления и т.д.). Критерий основан на предположении (нулевой гипотезе) об отсутствии разницы между величинами, полученными в результате выборочного наблюдения и теоретически вычисленными. Чем больше фактические величины отличаются от ожидаемых, тем больше уверенность, что изучаемый фактор оказывает существенное влияние.
Вычисляется критерий соответствия по формуле χ2 = 
Первым этапом в вычислении критерия соответствия являются формулировка нулевой гипотезы и исчисление ожидаемых величин. При определении ожидаемых чисел рекомендуется для большей точности расчета χ2 вычислять их до десятых. На следующем этапе определяется разность между фактическими и ожидаемыми числами по всем группам (φ – φ1). Затем определяют квадрат разностей (φ – φ1)2 и делят его на ожидаемое число в каждой группе  . Критерий соответствия определяется путем суммирования всех предыдущих результатов по всем группам. Полученную величину χ2 оцениваем по таблице критических значений (приложение 3), для чего определяют число степеней свободы n = (S – 1)(R – 1), где S – число строк, R – число рядов. Нулевая гипотеза подтверждается, если χ2 меньше критического (табличного значения), и опровергается, если полученная величина χ2 равна или больше табличного значения (приложение, табл. 4).
. Критерий соответствия определяется путем суммирования всех предыдущих результатов по всем группам. Полученную величину χ2 оцениваем по таблице критических значений (приложение 3), для чего определяют число степеней свободы n = (S – 1)(R – 1), где S – число строк, R – число рядов. Нулевая гипотеза подтверждается, если χ2 меньше критического (табличного значения), и опровергается, если полученная величина χ2 равна или больше табличного значения (приложение, табл. 4).
Пример расчета критерия соответствия (табл. 4).
1 этап – формулируем нулевую гипотезу – введение противогриппозной вакцины не повлияло на заболеваемость гриппом. В этом случае распределение на заболевших и не заболевших в двух группах наблюдения должно быть одинаковым и соответствовать итоговому распределению. Из 94 человек не заболел 61, а из 73 вакцинированных сколько могло быть не заболевших, если бы вакцинация не влияла на заболеваемость?

 =47,4
=47,4
Ожидаемое число заболевших среди вакцинированных будет определяться по пропорции: 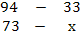
 =
=  =25,6
=25,6
Так же вычисляются ожидаемые величины для заболевших и не заболевших гриппом из числа не вакцинированных.
 =
= 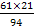 = 13,6
= 13,6  =
= 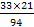 = 7,4
= 7,4
Таблица 4
§
| Число вакцинированных | Фактические числа (  ) ) | Ожидаемые числа (  ) ) | (φ – φ1) | (φ – φ1)2 |  | ||||||
| Не заболело | Заболело | Не заболело | Заболело | Не заболело | Заболело | Не заболело | Заболело | Не заболело | Заболело | ||
| Вакцинированы | 47,4 | 25,6 | 6,6 | -6,6 | 43,56 | 43,56 | 0,9 | 1,7 | |||
| Не вакцинированы | 13,6 | 7,4 | -6,6 | 6,6 | 43,56 | 43,56 | 3,2 | 5,9 | |||
| всего | Σ=11,7 |
Затем определяется разность между фактическими и ожидаемыми числами (φ – φ1) = 54 – 47,4= 6,6; 19 – 25,6 = – 6,6 и т.д.
Результаты возводятся в квадрат, и каждый из них делится на ожидаемое число в группе.

 и т.д.
и т.д.
χ2 определяется путем суммирования полученных результатов.
χ2 = 0,9 1,7 3,2 5,9 = 11,7
Для оценки критерия соответствия χ2 учитывается число рядов (R) и число строк (S) распределения фактических чисел (без итоговых), и на основании этих данных вычисляют так называемое число степеней свободы n = (R -1)×(S-1). Полученную величину χ2 оценивают по специальной таблице критических значений критерия соответствия χ2 (хи-квадрат). Для того, чтобы опровергнуть «нулевую гипотезу», вычисленный критерий соответствия должен быть равен или больше табличного (критического) значения при уровне вероятности «нулевой гипотезы» 95%.
Поскольку χ2 в нашем примере равен 11,7, что больше табличного значения при числе степеней свободы n = (2-1)х(2-1)=1, то нулевая гипотеза оказалась несостоятельна, следовательно, введение противогриппозной вакцины оказывает влияние на уровень заболеваемости гриппом.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задание №1. Вычислить критерий соответствия χ2 и определить, существенна или несущественна разность между числами, полученными в процессе статистического исследования, и «ожидаемыми величинами».
Задача 1
Установить, влияет ли семейное положение на успеваемость студентов.
| Семейное состояние | Успеваемость | Итого | ||
| отлично | хорошо | удовлетв | ||
| Не состоящие в браке | ||||
| Состоящие в браке | ||||
| Состоящие в браке и имеющие ребенка | ||||
| Всего наблюдений |
Задача 2
Установить, влияет ли участие в военных действиях на частоту возникновения посттравматических стрессовых расстройств у военнослужащих.
| Участие в военных действиях | Стрессовые расстройства | Итого | ||
| Значительно выражены | Незначительно выражены | Отсутствуют | ||
| Ветераны войны в Афганистане | ||||
| Участники войны в Чечне | ||||
| Не участвовали в военных действиях | ||||
| Всего обследовано |
Задача 3
Установить, влияют ли рекламные средства на решение пациентов обратиться к стоматологу.
Задача 4
Установить, влияет ли наличие инфекции Helicobacter pylori на частоту предопухолевой патологии и злокачественных новообразований желудка.
| Нозологическая форма заболевания | Количество наблюдений | Helicobacter pylori | |
| Присутствует | Отсутствует | ||
| Кишечная метаплазия | |||
| Дисплазия эпителия легкой ст. тяжести | |||
| Дисплазия эпителия средней степени тяжести | |||
| Дисплазия эпителия тяжелая | |||
| Рак желудка | |||
| Практически здоровые (контр. группа) | |||
| Всего |
Задача 5
Установить, влияет ли сезон на характер изменения веса у детей.
| Сезон года | Число обследованных детей | Прибавили в весе | Убавили в весе | Вес неизменен |
| Зима | ||||
| Весна | ||||
| Лето | ||||
| Осень | ||||
| Всего |
Задача 6
Установить влияет ли профессия на уровень распространенности клинических форм пограничных психических расстройств (ППР).
| Профессии | Неврозоподобные состояния | Неврозы и др. невротические расстройства | Без ППР | Всего |
| Аппаратчики | ||||
| Операторы | ||||
| Слесари | ||||
| Токари | ||||
| Всего |
Задача 7
Установить, влияет ли возраст на прием успокаивающих и снотворных средств.
| Возраст (лет) | Не принимают | Принимают иногда | Принимают постоянно | Итого |
| До 30 | ||||
| 31 – 40 | ||||
| 41 – 50 | ||||
| 51 – 60 | ||||
| 61 – 70 | ||||
| 71 и старше | ||||
| Всего |
Задача 8
Установить, влияет ли нозологическая форма заболевания на эффективность использования деминерализованных костных имплантатов в детской травматологии и ортопедии.
| Нозологическая форма заболевания | Количество наблюдений | Результат | |
| Положительный | Отрицательный | ||
| Опухолеподобные заболевания | |||
| Костная киста | |||
| Посттравматический псевдоартроз | |||
| Экзостозная дисхондроплазия | |||
| Несовершенный остеогенез | |||
| Первично-хронический остеомиелит | |||
| Лучевая косорукость | |||
| Юношеский эпифизеолиз | |||
| Всего |
Задача 9
Установить, влияет ли стаж работы на частоту возникновения гипертонической болезни у учителей.
| Стаж работы (лет) | Число наблюдаемых случаев | Всего | ||
| Гипертоническая болезнь 1 стадия | Гипертоническая болезнь 2-3 стадии | Без гипертонии | ||
| 1–5 лет | ||||
| 6 – 10 | ||||
| 11 – 15 | ||||
| 16 – 20 | ||||
| 21 – 25 | ||||
| Всего |
Задача 10
Установить, отличается ли состояние здоровья студентов, обучающихся на различных факультетах медицинских вузов.
| Факультет | Практически здоровые | Группа риска | Хронически больные | Всего наблюдений |
| Лечебный | ||||
| Педиатрический | ||||
| Стоматологический | ||||
| Медико-профилактический | ||||
| Сестринского дела | ||||
| Всего |
Задача 11
Установить, влияет ли семейное состояние на уровень физического развития детей младшего школьного возраста.
| Уровень физического развития | Всего наблюдений | |||||
| Низкий | Ниже среднего | Средний | Выше среднего | Высокий | ||
| Полная семья, соблюда-ющая здор. образ жизни | ||||||
| Семьи неблагополучные по алкоголизму | ||||||
| Не полная семья | ||||||
| Воспитанники детского дома | ||||||
| Всего |
Задача 12
Установить, влияет ли на характер течения язвенной болезни желудка тщательность выполнения пациентом рекомендаций врача.
| Течение заболевания | Рекомендации врача выполнялись: | Всего наблюдений | ||
| Полностью | Частично | Не выполнялись | ||
| Не осложненное | ||||
| Длительно не рубцующаяся язва | ||||
| Часто рецидивирующая язва | ||||
| Осложнено кровотечением | ||||
| Всего |
Задача 13
Установить, влияет ли кислотность желудочного сока на состояние крови у больных раком желудка.
| Кислотность желудочного сока | Нормальная кровь | Анемия легкой степени тяжести | Анемия средней степени тяжести | Тяжелая анемия | Всего |
| Ахлоргидрия | |||||
| Гипохлоргидрия | |||||
| Нормохлоргидрия | |||||
| Гиперхлоргидрия | |||||
| Всего больных |
Задача 14
Установить, влияет ли упитанность на умственное развитие ребенка.
| Степень упитанности | Коэффициент умственного развития | Всего | |||
| Ниже 80% | 80-89% | 90-99% | 100% и выше | ||
| Число детей с чрезмерной упитанностью | |||||
| Число детей с удовлетворит. упитанностью | |||||
| Число детей с неудовлетворительной упитанностью | |||||
| Всего наблюдений |
Рекомендуемая литература для студентов:
· Медик В.А., Юрьев В.К.Общественное здоровье и здравоохранение. Учебник для вузов: – М: ГЭОТАР – Медиа. – 2021, – 608 с.
· Медик В.А.Общественное здоровье и здравоохранение: Руководство к практическим занятиям: – М: ГЭОТАР – Медиа. – 2021, – 400 с.
· Щепин О.П., Медик В.А.Общественное здоровье и здравоохранение. Учебник для вузов: – М., 2021, – 592 с.
· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
· Серенко А.Ф., Ермаков В.В. Социальная гигиена и организация здравоохранения, М, 1984, с.139 – 149.
· Юрьев В.К., Куценко Г.И. Общественное здоровье и здравоохранение. С-П, 2000, с. 197 – 199.
· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова М. «МЕДпресс-информ»., 2002. – с. 108-109, 113-114.
· Зайцев В.М., Лифляндский В.Г., Маринкин В.И. Прикладная медицинская статистика. С.-П. «Фолиант», 2003.
§
ЦЕЛЬ ЗАНЯТИЯ: Освоить принципы измерения корреляционной связи и овладеть методикой измерения связи между явлениями.
Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно вычисляют коэффициенты корреляции по способу квадратов (Пирсона) и способу рангов (Спирмена); проводят оценки достоверности коэффициента корреляции. Оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Какие виды связи существуют между явлениями или признаками?
2. Является ли функциональная связь характерной для медико-биологических явлений?
3. Что такое корреляционная связь?
4. Можно ли считать, что при корреляционной связи значению одного признака соответствует несколько значений другого, взаимосвязанного с ним признака?
5. Можно ли утверждать, что корреляционная связь проявляется в массе наблюдений, т.е. в совокупности?
6. Что является критерием оценки характера и силы корреляции?
7. Можно ли утверждать, что коэффициент корреляции дает представление о наличии и направлении корреляционной связи?
8. С повышением температуры тела увеличивается частота пульса у большинства больных. Можно ли утверждать, что такая взаимосвязь относится к прямой корреляции?
9. Можно ли утверждать, что диапазон значений коэффициента корреляции находится в пределах от -1 до 1?
10. Каковы методы определения коэффициента корреляции?
11. Можно ли утверждать, что метод квадратов (Пирсона) дает более точные результаты по сравнению с методом рангов (Спирмена)?
12. Каков порядок определения коэффициента корреляции по методу рангов?
13. Как определяются характер и сила связи по коэффициенту корреляции?
14. Как оценивается достоверность коэффициента корреляции?
15. Можно ли утверждать, что если коэффициент корреляции более чем в три раза превышает свою ошибку, то он достоверен?
КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:
Задача каждой науки – вскрыть и изучить наиболее существенные связи между явлениями и процессами. Известны два вида связи между явлениями (признаками): функциональная и корреляционная. Функциональная связь отражает строгую зависимость процессов или явлений, и изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину. Функциональная связь, как правило, проявляется при физических и химических явлениях, где её можно представить в виде уравнения, формулы. Примером функциональной связи может являться увеличение объема шара в строгой зависимости от увеличения его радиуса, расширение тела по мере увеличения температуры нагревания и т.д. Корреляция – понятие, которое также означает взаимосвязь между признаками. При корреляционных связях, характерных для медико-биологических явлений, значению одного признака соответствуют разные значения других признаков. Корреляционная связь необходима, например, при оценке взаимосвязей между стажем работы и уровнем заболеваемости работающих; между разными уровнями физических факторов окружающей среды и состоянием здоровья; между различными уровнями интенсивности нагрузки и частотой (уровнем) физиологических реакций организма; между сроками госпитализации и частотой осложнений. Статистика позволяет исследователю измерить связи, обосновать выводы и наглядно их иллюстрировать. Корреляционная связь бывает положительной – прямой (при увеличении одного признака увеличивается другой) и отрицательной – обратной (при увеличении одного показателя другой уменьшается). Коэффициент корреляции свидетельствует не только о направлении связи, но и об уровне этой связи. Сильная связь выражается коэффициентом от 0,7 до 0,99, средняя — от 0,3 до 0,69, слабая — до 0,29. При нулевом значении коэффициента связи отсутствуют.
Наиболее простыми методом определения коэффициента корреляции являются ранговая корреляция:

, где

– коэффициент ранговой корреляции, d – разность рангов, n –число сопоставляемых пар признаков.При ранговой корреляции числовые выражения сравниваемых статистических рядов ранжируют, то есть проставляют ранговые номера для каждой цифры (от 1 и далее) и подставляют значения в формулу с учетом разницы порядковых значений.
Рассмотрим технику вычисления коэффициента ранговой корреляции на примере изучения связи между стажем работы (х) и числом травм (у):
| Стаж работы в годах | Число травм | Порядковые номера (ранги) | Разность рангов | Квадрат разности рангов | |
| X | Y | d(х-у) | d2 | ||
| До 1 года | -4 | ||||
| 1-2 | -2 | ||||
| 3-4 | 2,5 | 0,5 | 0,25 | ||
| 5-6 | 2,5 | 1,5 | 2,25 | ||
| 7 и более | 4 | ||||
| Σ d2 = 38,5 |
Коэффициент ранговой корреляции составит: 
Статистическая ошибка и критерий достоверности коэффициента корреляции вычисляются по формулам:
 = 0.22, t =
= 0.22, t =  = 0,925/0,22= 4,2
= 0,925/0,22= 4,2
Чтобы полученный коэффициент можно было считать достоверным, он должен превышать табличное значение (таблица значений критерия t по Н.А. Плохинскому) при числе степеней свободы n – 1. В нашем случае величина критерия t (4,2) значительно выше критического значения критерия t (2.7) для уровня значимости р = 0.05 и числа степеней свободы = n−1=4. Зависимость между стажем работы и числом травм по приведенным данным достоверно прослеживается. Вывод:поскольку коэффициент корреляции ρ = -0,925, корреляционная связь обратная, сильная, вероятность безошибочного прогноза выше 95%, следовательно, мы можем утверждать, что с увеличением стажа работы число травм у рабочих уменьшается.
При расчете коэффициента корреляции методом квадратов (метод Пирсона) сначала вычисляют среднее значение в каждом вариационном ряду сравниваемых групп. Затем находят отклонение каждой величины ряда от полученной средней. Для устранения отрицательных значений эти величины возводят в квадрат и подставляют в формулу: r
xy = 
, где d
x
и d
y
– отклонение каждой варианты от своей средней арифметической М
х
и М
y.
По величине коэффициента устанавливают направление и силу связи. Достоверность коэффициента определяют по таблицам критических значений (таблицам Каминского) при числе степеней свободы n’ = n-2 (приложение, табл. 4), а также при расчете средней ошибки и критерия достоверности t. Коэффициент корреляции должен превышать свою ошибку не менее чем в 3 раза. Формула ошибки коэффициента ранговой корреляции: m =

, t =

По методу Пирсона ошибка коэффициента корреляции вычисляется по формуле: m
r = 
, t =

. Значения t оценивается по таблице критических значений критерия t (при n<30, приложение, табл. 2).
Пример: определим направление и силу связи между количеством кальция в воде и жесткостью, если известны следующие данные
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) |
Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант. Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х (жесткость воды в градусах) и через у (количество кальция в воде в мг/л).
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) | dх | dу | dх × dу | dx2 | dy2 |
| -16 -12 -9 7 14 16 | -114 -86 -66 48 98 120 | |||||
| Мх=Σ х / n | Му=Σ у / n | Σdх×dу=7078 | Σdх2=982 | Σdy2=51056 | ||
| Мх=120/6=20 | Мy=852/6=142 |
1. Определить средние величины Mx ряду вариант “х” и Му в ряду вариант “у” по формулам: Мх = Σх/n (графа 1) и Му = Σу/n (графа 2).
2. Найти отклонение (dх и dу) каждой варианты от величины вычисленной средней в ряду “x” и в ряду “у” dх = V — Мх (графа 3) и dy = V — Му (графа 4).
3. Найти произведение отклонений dx х dy и суммировать их: Σ dх х dу (графа 5).
4. Каждое отклонение dx и dу возвести в квадрат и суммировать их значения по ряду “х” и по ряду “у”: Σ dx2 = 982 (графа 6) и Σ dy2 = 51056 (графа 7).
5. Определить произведение Σ dx2 х Σ dy2 и из этого произведения извлечь квадратный корень.
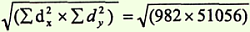
6. Полученные величины Σ (dx x dy) и √(Σdx2 x Σdy2) подставляем в формулу расчета коэффициента корреляции:
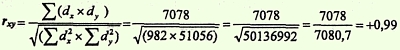
7. Определить достоверность коэффициента корреляции:
1-й способ. Найти ошибку коэффициента корреляции (mrxy) и критерий t по формулам:
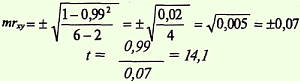
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р > 99,9%.
2-й способ оценки достоверности коэффициента корреляции. Достоверность коэффициента корреляции оценивается по таблице “Стандартные коэффициенты корреляции,считающиеся достоверными(по Л.С. Каминскому)” (приложение, табл. 4). При числе степеней свободы (n — 2) = 6 – 2 = 4 наш расчетный коэффициент корреляции rxу = 0,99 больше табличного (rтабл = 0,917 при р = 99%).
Вывод. Чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: rху = 0,99, р > 99,9%).
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
ЗАДАНИЕ 1: Вычислить коэффициент ранговой корреляции, определить направление и силу корреляционной связи, оценить достоверность полученных данных
Задача 1
Существует ли связь между стажем работы на машиностроительном предприятии и показателями заболеваемости рабочих?
| Стаж работы | До 1 года | 1-3 года | 4-5 лет | 6-10 лет | 11-15 лет | 16-20 лет | 21-25 лет | 26 и более |
| Число случаев заболеваний на 100 рабочих | 59,6 | 41,9 | 40,8 | 64,7 | 64,7 | 77,5 | 83,6 | 112,8 |
Задача 2
Существует ли связь между возрастом заболевших гриппом и уровнем смертности от этого заболевания?
| Возраст заболевших в годах | До 1 года | 1-4 | 5-9 | 10-14 | 15-17 | 18-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61 и старше |
| Смертность на 100000 человек | 68,3 | 57,7 | 55,9 | 24,7 | 55,9 | 42,1 | 67,9 | 86,6 | 89,4 | 106,7 | 158,2 |
Задача 3
Существует ли связь между возрастом мужчин и уровнем смертности?
| Возраст в годах | 0-4 | 5-9 | 10-14 | 15-24 | 25-34 | 35-44 | 45-54 | 55-64 | 65 и старше |
| Уровень смертности на 100000 человек | 801,0 | 272,0 | 194,7 | 296,8 | 624,1 | 922,8 | 2624,4 | 4324,5 | 9275,1 |
Задача 4
Существует ли связь между долей контингента часто болеющих (ЧБ) и возрастом детей?
| Возраст в годах | До 1 года | 1-2 | 3-4 | 5-6 | 7-8 | 9-10 | 11-12 | 13-14 |
| Доля ЧБ | 28,5 | 48,2 | 44,9 | 38,7 | 38,7 | 27,9 | 24,2 | 20,1 |
Задача 5
Существует ли связь между возрастом и частотой нарушения зрения у детей?
| Возраст в годах | 0-3 | 4-5 | 6-7 | 8-9 | 10-11 | 12-13 | 14-15 | 16-17 |
| Нарушения зрения, ‰ | 18,9 | 20,7 | 31,4 | 42,7 | 42,1 | 54,6 | 54,6 | 92,0 |
Задача 6
Существует ли связь между порядковым номером месяца года и частотой обращения населения за скорой и неотложной медицинской помощью по поводу сердечно-сосудистых заболеваний?
| Месяц | январь | февраль | март | апрель | май | июнь | июль | август | сентябрь | октябрь | ноябрь | декабрь |
| Частота обращений за СНМП ‰ | 114,3 | 108,3 | 109,7 | 103,2 | 104,5 | 95,2 | 98,4 | 97,8 | 87,6 | 92,7 | 92,7 | 96,4 |
Задача 7
Существует ли связь между расстоянием от места жительства до предприятия и заболеваемостью рабочих?
| Расстояние в метрах | До 500 м | 600-1000 | 1100-3000 | 3100-4000 | 4100-5000 | 5100-7000 | 7100-9000 | 9100 и более |
| Заболеваемость ‰ | 920,1 | 887,9 | 920,1 | 954,0 | 1286,3 | 1107,8 | 1510,8 | 1832,7 |
Задача 8
Существует ли связь между временем прошедшим от возникновения острого приступа холецистита до начала проведения операции и частотой послеоперационных осложнений?
| Время в часах | До 3 часов | 3-5 | 6-8 | 9-11 | 12-14 | 15-17 | 18-20 | 21-23 | 24 и более |
| Частота осложнений в % |
Задача 9
Существует ли связь между возрастной группой и частотой самоубийств у мужчин?
| Возрастная группа умерших, годы | До 20 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70 и старше |
| Частота самоубийств на 100 тыс. чел. | 4,1 | 28,5 | 43,8 | 54,8 | 54,8 | 48,2 | 75,5 |
Задача 10
Существует ли связь между возрастной группой мужчин и распространенностью психических заболеваний?
| Возрастная группа, годы | 0-4 | 5-9 | 10-14 | 15-19 | 20-24 | 25-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70 и старше |
| Заболеваемость ‰ | 16,2 | 35,4 | 31,2 | 8,1 | 10,2 | 35,0 | 31,4 | 53,1 | 58,8 | 30,5 | 19,2 |
Задача 11
Существует ли связь между возрастом ребенка и количеством больных с эквиноварусной деформацией стоп, обусловленной спастическими парезами в нижних конечностях?
| Возраст | До 1 месяца | 1- 3 месяца | 4 – 6 месяцев | 7-9 мес. | 10-12 мес. | 1-2 года | 2-3 года | Старше 3 лет |
| Кол-во больных |
Задача 12
Существует ли связь между возрастной группой и уровнем травматизма у мужчин?
| Возрастная группа мужчин, годы | Дети от 0 до 14 лет | 15-17 | 18-19 | 20-29 | 30-39 | 40-49 | 50-59 | 60-69 | 70 и старше |
| Частота травматизма на 100 тыс. чел. | 72,3 | 165,6 | 233,6 | 196,9 | 157,2 | 176,3 | 153,3 | 141,9 | 97,2 |
Задача 13
Существует ли связь между возрастом и уровнем смертности женщин в Российской Федерации?
| Возраст в годах | До 1 года | 1-4 | 5-9 | 10-14 | 15-24 | 25-34 | 35-44 | 45-54 | 55-64 | 65 и старше |
| Уровень смертности на 100000 человек | 10,9 | 0,7 | 0,3 | 0,3 | 0,85 | 1,8 | 3,6 | 7,7 | 15,4 | 113,9 |
Задача 14
Существует ли связь между возрастной группой пациентов и долей полностью удовлетворенных качеством лечения в стационаре?
| Возраст в годах | 15-20 | 21-25 | 26-30 | 31-35 | 36-40 | 41-45 | 46-50 | 51-55 | 56-60 | 61 и и старше |
| % удовлетворенных качеством лечения | 77,6 | 81,1 | 75,2 | 64,3 | 64,3 | 50,1 | 48,9 | 46,2 | 39,9 | 20,7 |
ЗАДАНИЕ 2: Вычислить коэффициент корреляции методом квадратов (Пирсона), определить направление и силу корреляционной связи, оценить достоверность полученных данных.
Задача 1
Существует ли связь между долей детей, охваченных прививками против кори, и уровнем заболеваемости корью?
| Охвачено прививками, % | |||||||
| Заболеваемость на 100 тыс. чел. |
Задача 2
Существует ли связь между ростом и массой тела у студентов-медиков в возрасте до 19 лет?
Задача 3
Существует ли связь между стажем работы в цехах с вредными условиями труда и кратностью заболеваемости с временной утратой трудоспособности?
| Стаж работы (лет) | ||||||||||
| Кратность случаев ВН (раз) |
Задача 4
Существует ли связь между длиной и массой тела у новорожденных?
| Длина, см | |||||||||||
| Масса, кг | 2,4 | 3,1 | 4,1 | 3,6 | 3,2 | 3,3 | 3,5 | 3,8 | 3,5 | 3,8 | 4,0 |
Задача 5
Существует ли связь между количеством бактерий, вырастающих при посеве 0,1 мл обеззараженной воды, и дозой остаточного хлора в 1 мл воды?
| Доза остаточного хлора (мг/л) | 0,05 | 0,10 | 0,07 | 0,60 | 2,00 | 1,00 | 0,80 | 1,2 | 3,00 |
| Число бактерий |
Задача 6
Существует ли связь между возрастом родильницы и количеством грудного молока?
| Возраст в годах | |||||||||||
| Лактация в гр |
Задача 7
Существует ли связь междудлительностью охлаждения организма и уровнем молочной кислоты (мг%)?
| Дни охлаждения | ||||||||||
| Уровень молочной кислоты мг% | 7,0 | 7,0 | 7,2 | 7,1 | 8,5 | 8,9 | 8,7 | 8,9 | 9,0 | 9,5 |
Задача 8
Существует ли связь между возрастом пациентов и потребностью их в медицинской помощи (эквивалентные единицы на 1 чел.)?
| Возраст в годах | ||||||||||
| Потребность в мед. помощи | 10,0 | 7,0 | 2,2 | 2,0 | 2,0 | 3,5 | 5,0 | 7,5 | 10,1 | 12,0 |
Задача 9.
Существует ли связь между температурой воздуха осенью и частотой возникновения ОРВИ?
Задача 10.
Существует ли связь между возрастом и заболеваемостью студентов медицинского университета?
| Возраст, лет | |||||||||
| Заболеваемость на 1000 чел. |
Рекомендуемая литература.
· Медик В.А., Юрьев В.К.Общественное здоровье и здравоохранение. Учебник для вузов: – М: ГЭОТАР – Медиа. – 2021, – 608 с.
· Медик В.А.Общественное здоровье и здравоохранение: Руководство к практическим занятиям: – М: ГЭОТАР – Медиа. – 2021, – 400 с.
· Щепин О.П., Медик В.А.Общественное здоровье и здравоохранение. Учебник для вузов: – М., 2021, – 592 с.
· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
· В.К. Юрьев, Г.И. Куценко. Общественное здоровье и здравоохранение. С.-П., 2000. –с.199-201.
· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002. –с. 110-112.
ТЕМА 7. Динамические ряды
ЦЕЛЬ ЗАНЯТИЯ: Овладеть методикой составления и обработки динамических рядов.
Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно преобразуют динамические ряды с целью выявления особенностей изучаемого процесса и достижения наглядности в характеристике того или иного явления, графически изображают полученные данные для определения тенденции изучаемого явления, рассчитывают показатели динамического ряда. Оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. В каких случаях обработки и анализа статистического материала прибегают к составлению динамических рядов? Что представляет собой динамический ряд?
2. Что такое уровни динамического ряда?
3. Какой динамический ряд называется простым и какой производным?
4. Что такое моментный динамический ряд?
5. Перечислите основные приемы выравнивания динамического ряда. Назовите составляющие анализа динамического ряда.
6. Какие показатели рассчитывают для анализа динамического ряда?
7. Почему для анализа динамического ряда его изображают графически?
КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:
В практическом здравоохранении или проведении медико-социальных исследований и в клинических работах часто требуется выявить основную закономерность изучаемого явления. В таких случаях, как правило, составляют динамический ряд. Динамический ряд — это ряд однородных статистических величин, показывающих изменение явления во времени. Динамический ряд может быть представлен абсолютными числами (изменение числа больных), средними величинами (среднее число лабораторных анализов за неделю) и относительными показателями (изменение рождаемости, заболеваемости, травматизма, обеспеченности врачами). Числа, из которых состоит динамический ряд, называются уровнями ряда. Если колебания уровней значительные, и выявить закономерность затруднительно, динамический ряд выравнивают. Существуют различные методы выравнивания динамического ряда: укрупнение интервалов, расчет скользящей средней и другие, позволяющие устранить влияние случайных колебаний на уровни динамического ряда.
Укрупнение интервала производят путем суммирования данных за ряд смежных периодов. Как видно из табл.5, помесячные числа заболеваний ангиной то увеличиваются, то уменьшаются. После укрупнения интервалов по кварталам года можно увидеть определенную закономерность, наибольшее число заболеваний приходится на летне-осенний период.
Таблица 5
Сезонные колебания случаев ангины в городе А. в 2021 г.
| Месяц | I | II | III | IV | V | VI |
| Число заболеваний по месяцам | ||||||
| по кварталам |
| VII | VIII | IX | X | XI | XII | Итого за2021 г. |
Вычисление групповой средней для каждого укрупненного периода производят так: суммируют смежные уровни соседних периодов, а затем полученную сумму делят на число слагаемых (табл. 6).
Таблица 6
Динамика процента расхождений клинических и патологоанатомических диагнозов по данным больницы города А.
| Годы | ||||||||
| Процент расхож- дения диагнозов | 11,0 | 9,8 | 8.0 | 9,2 | 8,2 | 8,6 | 8,5 | 7,9 |
| Групповая средняя | 10,4 | 8,6 | 8,4 | 8,2 |
Для уровней динамического ряда, представленных в табл. 6, характерны волнообразные колебания. Выравнивание ряда путем вычисления групповой средней позволило получить данные, иллюстрирующие довольно четкую тенденцию к постепенному снижению процента расхождений диагнозов в больнице.
Вычисление скользящей средней позволяет каждый уровень заменить на среднюю величину из данного уровня и двух соседних с ним (табл. 7).
Ряд, выровненный при помощи скользящей средней, представляет последовательную тенденцию снижения процента расхождения диагнозов. Таким образом, скользящая средняя является простейшим способом выравнивания ряда. Этот метод дает возможность сгладить, устранить резкие колебания динамического ряда.
Таблица 7
Методика расчета скользящей средней
| Годы | ||||||||
| Процент расхож- дения диагнозов | 11,0 | 9,8 | 8.0 | 9,2 | 8,2 | 8,6 | 8,5 | 7,9 |
| Скользящая средняя | – | 9,6 | 9,0 | 8,7 | 8,6 | 8,4 | 8,3 | – |
Ряд, выровненный с помощью скользящей средней, иллюстрирует общую четкую тенденцию: постепенное уменьшение показателей частоты расхождения диагнозов.
Анализ динамического (временного) ряда сводится к вычислению следующих показателей: абсолютного прироста (или снижения); темпа роста (или снижения); темпа прироста; значения 1% прироста, показателей наглядности. Абсолютный прирост представляет собой разность между последующим и предыдущим уровнем. Темп роста — это отношение последующего уровня к предыдущему, умноженное на 100%. Темп прироста является отношением абсолютного прироста (снижения) к предыдущему уровню, умноженным на 100%. Значение 1% прироста определяется отношением абсолютного прироста к темпу прироста. Показатель наглядности показывает отношение каждого уровня ряда к одному из них (чаще начальному), принятому за 100%.
1) Абсолютный прирост или убыль (абсолютный размер разности уровней) – разность между последующим и предыдущим уровнями (дает возможность анализировать скорость происходящих изменений в ее абсолютном выражении).
2) Темп прироста или убывания – процентное отношение абсолютного прироста (или снижения) к предыдущему уровню.
3) Темп роста или снижения – процентное отношение последующего уровня к предыдущему.
4) Для анализа динамического ряда используются также показатели наглядности, хотя следует помнить, что для коэффициента наглядности не обязательны взаимосвязанные динамические изменения.
Динамические ряды характеризуют изменение показателей здоровья – уровень и темп снижения заболеваемости, демографические сдвиги (рождаемости, общей и младенческой смертности), изменения физического развития. Пример анализа динамического ряда (табл. 8).
Таблица 8
Динамика рождаемости в сельском поселении за 2021 – 2021 гг.
| Год | Число родившихся на 1000 населения | Абсолютный прирост | Темп прироста | Темп роста | Показатель наглядности |
| 8,7 8,9 8,8 8,5 8,3 | – 0,2 -0,1 -0,3 -0,2 | – 2,6% -1,3% -3,8% -2,7% | – 102,6% 98,7% 96,2% 97,3% | 100,0% 102,6% 101,3% 97,4% 94,8% |
Расчет показателей динамического ряда:
1) Абсолютный прирост: 8,9 – 8,7 = 0,2
8,8 – 8,9 = – 0,1 и т.д.
2) Темп прироста: 0,2: 8,7 × 100% = 2,3%
-0,1: 8,9 × 100% = – 1,1% и т.д.
3) Темп роста: 8,9: 8,7 × 100% = 102,3%
8,8: 8,9 × 100% = 98,87% и т.д.
4) Показатель наглядности: уровень 2021 г. принимаем за 100%
8,9: 8,7 ×·100% = 102,3%
8,8: 8,7 × 100% = 101,1% и т.д.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
§
Вычислите показатели динамического ряда – абсолютный прирост, показатели роста, темп прироста, показатели наглядности.
Задача 1
Заболеваемость туберкулезом на 100 тысяч населения в Российской Федерации.
| Годы | ||||||||||
| Заболеваемость | 66,8 | 68,0 | 75,4 | 82,6 | 83,3 | 85,1 | 82,6 | 77,2 | 73,0 | 68,1 |
Задача 2
Динамика рождаемости в Российской Федерации.
| Годы | ||||||||||
| Общая рождаемость, ‰ | 10,2 | 10,4 | 10,2 | 10,4 | 11,3 | 12,1 | 12,4 | 12,5 | 12,6 | 12,6 |
Задача 3
Динамика общей смертности населения Ставропольского края.
| Годы | ||||||||||
| Общая смертность, ‰ | 14,9 | 14,3 | 14,4 | 14,2 | 13,3 | 13,4 | 13,2 | 12,4 | 12,3 | 12,6 |
Задача 4
Динамика сети самостоятельных детских больниц в РФ.
| Годы | |||||||||||
| Детские больницы, всего |
Задача 5
Динамика развития дневных стационаров в системе педиатрической помощи детям.
| Годы | ||||||||||
| Число детских дневных стационаров всех типов |
Задача 6
Динамика показателя младенческой смертности в Российской Федерации.
| Годы | ||||||||||
| Младенческая смертность на 1000 детей, родившихся живыми | 12,4 | 11,6 | 11,0 | 10,2 | 9,4 | 8,5 | 8,1 | 7,5 | 7,4 | 8,6 |
Задача 7
Среднемесячная заработная плата работников здравоохранения Ставропольского края.
| Годы | ||||||||||
| Тыс. руб | 3,2 | 4,2 | 5,7 | 7,0 | 8,7 | 8,9 | 11,8 | 11,2 | 13,0 | 14,1 |
Задача 8
Динамика общей заболеваемости новорожденных в Ставропольском крае.
Задача 9
Летальность от отравлений в стационарах Ставропольского края (%).
| Годы | ||||||||||
| Уровень летальности | 4,2 | 4,3 | 4,6 | 3,2 | 4,7 | 2,5 | 4,3 | 4,9 | 3,4 | 3,0 |
Задача 10
Динамика первичного выхода на инвалидность в трудоспособном возрасте в Ставропольском крае (на 10 тыс. соответствующего населения).
| 67,2 | 67,8 | 72,5 | 76,9 | 59,1 | 56,3 | 56,1 | 64,3 | 60,3 | 53,1 |
Задача 11.
Среднее число дней пребывания больного (дети 0-17) на койке в Ставропольском крае.
| Годы | ||||||||||
| Инфекционные и паразитарные болезни | 11,2 | 10,4 | 10,7 | 10,2 | 9,4 | 8,5 | 9,5 | 8,6 | 8,6 | 8,3 |
Задача 12.
Число больничных коек для беременных в Ставропольском крае.
Рекомендуемая литература
· Медик В.А., Юрьев В.К.Общественное здоровье и здравоохранение. Учебник для вузов: – М: ГЭОТАР – Медиа. – 2021, – 608 с.
· Медик В.А.Общественное здоровье и здравоохранение: Руководство к практическим занятиям: – М: ГЭОТАР – Медиа. – 2021, – 400 с.
· Щепин О.П., Медик В.А.Общественное здоровье и здравоохранение. Учебник для вузов: – М., 2021, – 592 с.
· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
· В.К. Юрьев, Г.И. Куценко. Общественное здоровье и здравоохранение. (Учебник для студентов, интернов, аспирантов, ординаторов педиатрических факультетов), Санкт-Петербург. 2000. –с. 204-212.
· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002. –с. 92-97.
ТЕМА 8. Использование метода стандартизации при оценке здоровья населения и показателей работы учреждений здравоохранения
ЦЕЛЬ ЗАНЯТИЯ: Овладеть прямым методом стандартизации.Уметь рассчитывать интенсивные, ожидаемые (условные) и стандартизованные показатели, анализировать и сопоставлять интенсивные и стандартизованные показатели, делать вывод.
Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно овладевают прямым методом стандартизации, рассчитывают интенсивные, ожидаемые и стандартизированные (гипотетические) показатели. Анализируют и сопоставляют интенсивные и стандартизованные показатели, оценивают полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. В каких случаях применяется метод стандартизации?
2. В чем заключается сущность прямого метода стандартизации?
3. В каких случаях применяется прямой метод стандартизации, а в каких косвенный и обратный?
4. Назовите этапы прямого метода стандартизации.
5. Какова методика расчета интенсивных, ожидаемых и стандартизованных показателей?
6. Какова методика сопоставления и анализа интенсивных и стандартизованных показателей.
КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ
Во многих медико-социальных, а также в клинических исследованиях, как правило, исключена возможность получения однородных групп для сравнения тех или иных показателей. Это касается, в первую очередь, показателей заболеваемости, общей смертности, рождаемости по городам, районам, странам, имеющих разный состав населения по возрасту, полу и т.д. В таких случаях широкое применение находит метод стандартизации, который позволяет исключить влияние на общий показатель разного состава совокупностей по одному, двум или более признакам.
Метод стандартизации используется при оценке показателей здоровья только при сравнении их уровней. Этот метод расчета условных величин применяется для устранения неоднородности состава сравниваемых коллективов. Он показывает, какой был бы уровень заболеваемости (травматизма, смертности, инвалидности и др.) в каждом коллективе (учреждении, городе), если бы его состав (по возрасту, по полу, по трудовому стажу и др.) был одинаков. Стандартизованные показатели используют при необходимости сравнения уровней смертности (заболеваемости) от злокачественных заболеваний (болезней органов пищеварения и т. д.) в разных городах, районных центрах, если сравниваемые группы населения неоднородны по возрасту или полу; уровней заболеваемости (травматизма) на разных производствах, если профессиональный состав работников неоднороден; уровней летальности в разных больницах (отделениях) при неоднородности пациентов этих ЛПУ по тяжести течения заболевания. Метод позволяет установить влияние одного из факторов (пол, возраст, тяжесть заболевания, условия труда, образ жизни, факторы окружающей среды), на различие уровней заболеваемости или других показателей здоровья. Существует 3 способа стандартизации: прямой, косвенный и обратный. Прямой способ применяют, когда имеются погрупповые (повозрастные) показатели заболеваемости (смертности, травматизма), или их можно вычислить (при наличии погрупповой численности населения и заболевших). Косвенный способ используют, если показатели по группам отсутствуют, и их нельзя вычислить из-за отсутствия числа заболевших. Обратный способ применяют при отсутствии погрупповых величин численности населения. Общим этапом вычисления стандартизованных коэффициентов является выбор стандарта возрастно-полового состава (процентное распределение состава любой из сравниваемых групп или их суммарного значения). При выборе стандартного состава уровня заболеваемости можно использовать литературные данные или показатели предыдущих исследований.
Наиболее распространенным является прямой метод стандартизации. Прямой метод состоит из 5 этапов.
I этап – расчет общих и специальных (по каждой группе – половой, возрастной и др.) интенсивных показателей (или средних величин) для двух сравниваемых совокупностей.
II этап – выбор и расчет стандарта.
III этап – расчет «ожидаемых величин» для каждой группы стандарта.
IV этап — определение стандартизированных показателей.
V этап – сравнение групп по общим интенсивным (или средним) и стандартизованным показателям. Выводы.
Целесообразно все эти расчетные операции представить в виде этапов стандартизации и оформить их в виде таблицы.
Рассмотрим технику вычисления стандартизированных показателей на примере изучения воздействия биологически активных добавок к пище (БАД) на здоровье человека. Исследование проводилось на группе волонтеров (группа В.), а для сравнения была взята контрольная группа (группа К.). Результаты представлены в таблице 9.
На I этапе стандартизации требуется определить, как часто встречаются заболевания среди испытуемых в группах В. и К. Для этого вычисляют специальные интенсивные показатели, т.е. процент имевших заболевания в каждой группе отдельно. Расчет ведется следующим образом: число больных надо разделить на соответствующее число испытуемых и умножить на 100. В контрольной группе заболеваемость мужчин составила 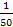 ×100=2,0%, а женщин –
×100=2,0%, а женщин – 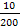 ×100 = 5,0%.
×100 = 5,0%.
Подобные же расчеты надо сделать для группы волонтеров.
Таблица 9
Заболеваемость в группе лиц, употреблявших биологически активные добавки к пище, и контрольной группе
| Пол | Группа К. | Группа В. | I этап | II этап | III этап | ||||
| Кол-во человек | Число заболев. | Кол-во человек | Число заболев. | % заболевших | Стандарт | Ожидаемые числа | |||
| К | В. | К. | В. | ||||||
| Муж. | 2,0 | 2,3 | 4,4 | 5,06 | |||||
| Жен. | 5,0 | 10,0 | 11,5 | 23,0 | |||||
| Итого | 4,4 | 3,3 | Σ = 15,9 | Σ = 28,06 | |||||
| IV этап | 3,5% | 6,2% |
Всего же заболеваемость лиц в контрольной группе составила  ×100 = 4,4%, а в группе волонтеров – 3,3%. Анализ интенсивных показателей позволяет предположить, что уровень заболеваемости в группе людей, принимавших БАД, ниже, чем в контрольной группе. Однако из табл. 9 (I этап) видно, что у мужчин и женщин контрольной группы реже встречаются заболевания, чем у мужчин и женщин, принимавших БАД, хотя в целом по строке («итого») в двух группах отмечено противоположное соотношение показателей: общий процент больных больше в контрольной группе, а не в группе волонтеров. Этот факт объясняется тем, что на общие показатели по каждой группе оказал влияние разный по полу состав лиц, охваченных испытанием. Так, в составе контрольной группе было больше женщин (а среди женщин чаще встречаются заболевания, чем среди мужчин). Большую часть группы волонтеров составляли мужчины, которые менее внимательны к своему здоровью и реже обращаются к врачам по поводу заболеваний. Следовательно, в данном случае различие в общих итоговых интенсивных показателях, полученных по двум группам, может быть связано с неоднородностью их полового состава.
×100 = 4,4%, а в группе волонтеров – 3,3%. Анализ интенсивных показателей позволяет предположить, что уровень заболеваемости в группе людей, принимавших БАД, ниже, чем в контрольной группе. Однако из табл. 9 (I этап) видно, что у мужчин и женщин контрольной группы реже встречаются заболевания, чем у мужчин и женщин, принимавших БАД, хотя в целом по строке («итого») в двух группах отмечено противоположное соотношение показателей: общий процент больных больше в контрольной группе, а не в группе волонтеров. Этот факт объясняется тем, что на общие показатели по каждой группе оказал влияние разный по полу состав лиц, охваченных испытанием. Так, в составе контрольной группе было больше женщин (а среди женщин чаще встречаются заболевания, чем среди мужчин). Большую часть группы волонтеров составляли мужчины, которые менее внимательны к своему здоровью и реже обращаются к врачам по поводу заболеваний. Следовательно, в данном случае различие в общих итоговых интенсивных показателях, полученных по двум группам, может быть связано с неоднородностью их полового состава.
Для элиминирования (устранения) косвенного влияния на показатели заболеваемости разного состава двух групп по полу необходимо провести стандартизацию.
II этап. Выбор и расчет стандарта. За стандарт следует принимать тот состав совокупностей, в котором отразились бы все особенности состава сравниваемых групп. В нашем примере за такой стандарт принята суммарная численность лиц, охваченных исследованием (графа 1 – графа 3). Стандартом для группы мужчин будет 220 (50 170), а для женщин – 230 (200 30). Общее число лиц в двух группах составит 450. Зная интенсивные показатели (I этап) и стандарт (II этап), можно перейти к III этапу – определению «ожидаемого числа» заболеваемости в каждой группе стандарта.
III этап. Определение «ожидаемых чисел» больных в каждой группе стандарта. Порядок вычисления «ожидаемых чисел» можно показать на следующем примере. В контрольной группе заболеваемость мужчин, больных гепатитом, 2%. Сколько было бы больных мужчин среди 220 человек при данном уровне заболеваемости? Составим пропорцию и произведем расчет. Аналогично вычисляют «ожидаемое число» заболеваемости у женщин в контрольной группе.
Такие же расчеты произведем по группе волонтеров.
Таким образом, 4,4 — «ожидаемое число» заболеваний у 220 мужчин, не употреблявших биологически активные добавки к пище, а у применявших БАД «ожидаемое» число заболевших у 220 мужчин составляет 5,06.
Такой же принцип расчета «ожидаемых чисел» заболеваний для женщин. После расчета всех ожидаемых чисел переходим к IV этапу.
IV этап. Определение стандартизованных показателей. Прежде всего, необходимо просуммировать абсолютные «ожидаемые» числа заболеваний мужчин и женщин по каждой группе отдельно. Полученные суммы относят к общей численности участвующих в исследовании лиц, указанной в итоговой строке стандарта. Это отношение выражают в процентах и получают стандартизованные показатели. Так, в группе К. сумма «ожидаемых» чисел больных составит: 4,4 11,5 = 15,9. Стандартизованный показатель заболеваемости в группе К. равен:
В группе В. сумма «ожидаемых» чисел больных составит 5,06 23,0=28,06; стандартизованный показатель заболеваемости в группе В. равен
V этап. Сравнение уровней заболеваемости в группах К. и В. по стандартизованным и общим интенсивным показателям. Для этого следует выписать стандартизованные и интенсивные показатели в отдельную аналитическую таблицу (табл. 10), сопоставить эти данные и сделать общий вывод. Вывод. Сравнение стандартизованных показателей, рассчитанных для двух исследуемых групп, позволяет сделать заключение, что при одинаковом по полу составе лиц в группе волонтеров и контрольной группе показатель заболеваемости в контрольной группе не употреблявших БАД значительно ниже, чем в группе использующих эти препараты.
Таблица 10
Сопоставление уровней заболеваемости гепатитом рабочих в группах К. и В. (%)
| Показатели | Группа контрольная | Группа волонтеров | Результаты сравнения |
| Стандартизованные | 3 5 | 6,2 | К<В |
| Общие интенсивные (грубые) | 4,4 | 3,3 | К>В |
При сравнении общих (грубых) интенсивных показателей результаты получились противоположными (К.>В.) в связи с тем, что на общие интенсивные показатели оказал влияние разный состав исследуемых по полу. Произошло это оттого, что у женщин значительно выше заболеваемость, чем у мужчин, а в группе К. преобладали женщины, тогда как в группе В. – мужчины.
Метод стандартизации необходимо применять при:
1) значительных различиях в уровнях групповых показателей (разные уровни заболеваемости мужчин, женщин, разные уровни летальности по отделениям больниц, различная средняя длительность лечения по заболеваниям и т. д.).
2) значительной неоднородности составов сравниваемых совокупностей.
Если показатели по отдельным группам почти одинаковы, то при различном составе изучаемых совокупностей по этим группам стандартизацию проводить не нужно. Если показатели по группам разные, а состав одинаков, то стандартизация также не имеет смысла. Пользуясь методом стандартизации, необходимо иметь в виду, что стандартизованные показатели являются условными по своей сути и не могут дать представления об истинном размере явления. Поэтому взятый изолированно стандартизованный показатель не имеет смысла. Основная ценность стандартизованных показателей заключается в том, что они дают возможность элиминировать влияние на уровни показателей разных составов совокупностей и позволяют ответить на вопрос, какова была бы величина изучаемого явления при условии исключения влияния неоднородности состава сравниваемых совокупностей.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
§
Задача 1
Сравнить показатели летальности в двух группах больных СПИДом, получавших различные лекарственные препараты, с показателями, стандартизованными по тяжести течения заболевания. За стандарт принять сумму составов больных, получивших различное лечение.
| Тяжесть течения заболевания | Новое средство | Традиционное лечение | ||
| Число больных | Из них умерло | Число больных | Из них умерло | |
| Очень тяжелое | ||||
| Тяжелое | ||||
| Средней тяжести | ||||
| Легкое | ||||
| Всего |
Задача 2
Сравнить показатели летальность в двух педиатрических отделениях больницы с показателями, стандартизованными по возрасту. За стандарт принять сумму составов детей, прошедших лечение в больнице.
| Возраст детей | Отделение № 1 | Отделение № 2 | ||
| Число больных | Из них умерло | Число больных | Из них умерло | |
| 0 – 6 месяцев | ||||
| 7– 12 месяцев | ||||
| 1 – 2 года | ||||
| 3- 4 года | ||||
| 5 – 6 лет | ||||
| 7 – 8 | ||||
| 9 и старше | ||||
| Всего |
Задача 3
Сравнить показатели заболеваемости работников заводоуправления и основных цехов предприятия с показателями, стандартизованными по уровню дохода. За стандарт принять сумму составов работников заводоуправления и основных цехов предприятия.
| Уровень дохода | Заводоуправление | Основные цеха | ||
| Число работников | Число заболеваний | Число работников | Число заболеваний | |
| Высокий | ||||
| Выше среднего | ||||
| Средний | ||||
| Ниже среднего | ||||
| Низкий | ||||
| Всего |
Задача 4
Сравнить показатели травматизма на двух машиностроительных предприятиях с показателями, стандартизованными по характеру труда. За стандарт принять сумму составов рабочих на двух предприятиях.
| Характер труда | Предприятие «Сатурн» | Предприятие «Восток» | ||
| Число рабочих | Число травм | Число рабочих | Число травм | |
| Автоматизированный | ||||
| Механизированный | ||||
| Ручной труд | ||||
| Всего |
Задача 5
Сравнить показатели рождаемости в двух городах Ставропольского края с показателями, стандартизованными по возрасту. За стандарт принять полусумму возрастных составов женщин в двух городах.
| Возрастной состав женщин | Город Светлоград | Город Изобильный | ||
| Число женщин | Число родившихся детей | Число женщин | Число родившихся детей | |
| 16-19 | ||||
| 20-24 | ||||
| 25-29 | ||||
| 30-39 | ||||
| 40-49 | ||||
| Всего |
Задача 6
Сравнить уровень рождения маловесных детей в городской и сельской местности с показателями, стандартизованными по социальным факторам риска. За стандарт принять число детей, родившихся в городской местности.
| Социальные факторы риска | Городская местность | Сельская местность | ||
| Число новорожденных | Масса тела при рождении менее 1500 г | Число новорожденных | Масса тела при рождении менее 1500 г | |
| Плохое материальное положение семьи | ||||
| Плохие жилищно-бытовые условия | ||||
| Алкоголизм родителей | ||||
| Наркомания родителей | ||||
| Курение | ||||
| Всего |
Задача 7
Сравнить показатели смертности в г. Минеральные Воды и Минераловодском районе с показателями, стандартизованными по возрастному составу населения. За стандарт принять возрастной состав населения Минераловодского района.
| Возраст в годах | г. Минеральные Воды | Минераловодский район | ||
| Число лиц | Число умерших | Число лиц | Число умерших | |
| 25-34 | ||||
| 35-44 | ||||
| 45-54 | ||||
| 55-64 | ||||
| 65 и старше | ||||
| Всего |
Задача 8
Сравнить показатели заболеваемости в двух цехах предприятия с показателями, стандартизованными по возрастному составу рабочих. За стандарт принять возрастной состав рабочих обоих цехов.
| Возраст рабочих в годах | Механосборочный цех | Литейный цех | ||
| Число рабочих | Число случаев заболеваний | Число рабочих | Число случаев заболеваний | |
| До 20 лет | ||||
| 20-29 | ||||
| 30-39 | ||||
| 40-49 | ||||
| 50-59 | ||||
| Всего |
Задача 9
Сравнить показатели заболеваемости детей, посещающих дошкольные учреждения и воспитывающихся дома, с показателями, стандартизованными по возрасту. За стандарт принять возрастной состав детей в обеих группах.
| Возрастные группы | Дети, посещающие детские сады | Дети, воспитывающиеся дома | ||
| Число детей | Случаи ОРВИ | Число детей | Случаи ОРВИ | |
| До 1 года | ||||
| 1- 3 года | ||||
| 4-5 лет | ||||
| 6-7 лет | ||||
| Всего |
Задача 10
Сравнить показатели заболеваемости кариесом детей, воспитывающихся дома и в интернате, с показателями, стандартизованными по возрасту. За стандарт принять сумму составов детей в двух обследованных группах.
| Возраст детей, годы | Дети, воспитывающиеся дома | Дети, воспитывающиеся в интернате | ||
| Число детей | Число заболеваний | Число детей | Число заболеваний | |
| 4 – 6 лет | ||||
| 7 – 9 | ||||
| 10-12 | ||||
| 13- 15 | ||||
| Всего |
Задача 11
Сравнить распространенность пародонтоза в городской и сельской местности с показателями, стандартизованными по возрасту. За стандарт принять возрастной состав городского населения.
| Возраст, годы | Городская местность | Сельская местность | ||
| Число обследованных | Число больных | Число обследованных | Число больных | |
| 0-19 | ||||
| 20-39 | ||||
| 40-59 | ||||
| 60 и старше | ||||
| Всего |
Задача 12
Сравнить частоту осложнений в родах у первородящих и повторнородящих женщин и сопоставить эти показатели со стандартизованными по возрасту. За стандарт принять сумму составов первородящих и повторнородящих женщин.
| Возраст женщины, годы | Первородящие | Повторнородящие | ||
| Число женщин | Число осложнений | Число женщин | Число осложнений | |
| До 20 лет | ||||
| 21 – 25 | ||||
| 26- 35 | ||||
| 36 и старше | ||||
| Всего |
Рекомендуемая литература:
· Медик В.А., Юрьев В.К.Общественное здоровье и здравоохранение. Учебник для вузов: – М: ГЭОТАР – Медиа. – 2021, – 608 с.
· Медик В.А. Общественное здоровье и здравоохранение: Руководство к практическим занятиям: – М: ГЭОТАР – Медиа. – 2021, – 400 с.
· Щепин О.П., Медик В.А.Общественное здоровье и здравоохранение. Учебник для вузов: – М., 2021, – 592 с.
· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
· В.К.Юрьев, Г.И.Куценко. Общественное здоровье и здравоохранение. Санкт-Петербург.2000 (учебник для студентов, интернов, аспирантов, ординаторов педиатрических факультетов). – с. 201-204.
· Ю.П.Лисицын. Общественное здоровье и здравоохранение. Учебник для вузов. Москва. 2002. – с. 305-307.
· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002.
ТЕМА 9. ДЕМОГРАФИЯ, ЕЁ МЕДИКО-СОЦИАЛЬНЫЕ АСПЕКТЫ
ЦЕЛЬ Занятия: Овладение методами расчета демографических показателей, анализа демографической ситуации и разработки мер по её улучшению.
Методика проведения занятия: Студенты самостоятельно готовятся к практическому занятию по рекомендованной литературе и выполняют индивидуальное домашнее задание. Преподаватель в течение 10 минут проверяет правильность выполнения домашнего задания и указывает на допущенные ошибки, проверяет степень подготовки с использованием тестирования и устного опроса. Затем студенты самостоятельно овладевают методикой расчета и оценки демографических показателей. Анализируют полученные данные и формулируют заключение. В конце занятия преподаватель проверяет самостоятельную работу студентов.
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Что изучает демография? Какие разделы в этой науке выделяют?
2. Что изучает статика населения?
3. Какой метод используется для получения сведений о численности и составе населения?
4. Как изменяется численность населения в мире и РФ? Что можно предпринять для оптимизации численности населения в стране?
5. Какие сведения дает всеобщая перепись о составе населения? Как изменяется состав населения в РФ?
6. Какие виды движения населения существуют?
7. Назовите основные показатели естественного движения населения.
8. Как проводится учет рождаемости и смертности в нашей стране?
9. Как вычисляются и оцениваются общие и специальные показатели рождаемости?
10. Как вычисляются и оцениваются общие и специальные показатели смертности?
11. Как вычисляются и оцениваются показатели смертности в детском возрасте?
12. Каковы основные причины общей, повозрастной, младенческой смертности?
13. В чём заключаются особенности современной демографической ситуации в России и Ставропольском крае?
14. Какими причинами обусловлена современная демографическая ситуация?
15. Какие меры можно предложить для улучшения демографической ситуации в стране?
КРАТКОЕ СОДЕРЖАНИЕ ТЕМЫ:
Среди параметров общественного здоровья важнейшее место занимают медико-демографические показатели, которые наиболее полно отражают диапазон воздействующих на популяционное здоровье факторов социально-экономического, политического, поведенческого, природно-климатического и экологического генеза и в силу этого являются максимально адекватными измерителями народного благополучия и общественного здоровья.
Демография – наука о народонаселении и его общественном развитии, которая включает два раздела: статика населения и динамика населения. Статика изучает численность и состав населения на определенный (критический) момент времени, источником сведений о которых служат регулярно проводимые переписи. Попытки провести всеобщую перепись населения предпринимались ещё в древнем Китае, Египте, Индии и других древних цивилизациях. Первая документально подтвержденная всеобщая перепись была проведена в 1790 году в США, а затем в 1801 году в Европе (Англии, Франции, и Дании).
В России впервые перепись прошла в 1897 году, подготовка к которой велась почти 40 лет. Последующие переписи состоялись в 1920, 1926, 1937, 1959, 1970, 1979, 1989 и 2002 годы; последняя перепись прошла с 14 по 25 октября 2021г. По данным последней переписи населения в России проживает 141,9 млн. человек, из них: городских жителей – 103,7 млн. человек, а сельских –38,2 млн. человек.
В настоящее время практически во всех странах мира всеобщие переписи населения проходят один раз в 10 лет. Результаты всеобщих переписей указывают на растущую численность населения нашей планеты. Причем особенно интенсивно численность населения увеличивалась в XX веке. Если, например, на протяжении XVII – XIX веков население увеличивалось не более чем на 0,5% в год, то в дальнейшем заметное нарастание темпов прироста отмечается буквально по десятилетиям. С 1930 по 1940 год население земного шара ежегодно увеличивалось на 1%, к 1950 году этот показатель приблизился к 2%, а в 1970 году достиг 3%.
Столь высокие темпы роста численности населения объясняются резким увеличением его численности в развивающихся странах Африки, Азии и Латинской Америки. Многие ученые считают, что если рост численности населения будет продолжаться такими же темпами, то через сравнительно небольшой промежуток времени человечество не сможет существовать на ограниченных территориях нашей планеты из-за отсутствия продовольствия и экологических загрязнений. Однако безудержный рост численности населения можно приостановить проведением грамотной демографической политики, призванной регулировать рождаемость и тем самым воздействовать на численность населения в стране. Одним из первых государств, осуществляющих жесткую демографическую политику по ограничению рождаемости, стал Китай, где введена прогрессивная система налогообложения при рождении второго и последующих детей.
Россия в 2002 году занимала седьмое место в мире по численности населения после Китая (1285 млн. чел.), Индии (1025 млн. чел), США (286 млн. человек), Индонезии (215 млн. человек), Бразилии (173 млн. человек) и Пакистана (146 млн. человек). Численность постоянного населения Российской Федерации составляла в 2002году 145,2 млн. человек и по сравнению с переписью 1989 года уменьшилась на 1,8 млн. человек.
Плотность населения – еще один результат переписи населения. Наиболее плотно населенные страны — это страны Азии: Япония, Южная Корея, Пакистан, Индия. В этих странах плотность населения достигает 200—500 человек на 1 кв. км. В мегаполисах, например, в Сеуле, Токио или Мехико, плотность населения составляет до 700 человек на 1 кв. км. В странах Европы плотность — около 100 человек на 1 кв. км. Учитывая, что в России очень большие «запасы» территории, плотность населения невысока и составляет в среднем 8,7 жителя на 1 кв. км. Кроме того, плотность населения в РФ существенно колеблется по регионам. Так, плотно заселена европейская часть – до 100 человек на один квадратный километр, а в районах крайнего Севера плотность не всегда достигает 1 человека на 1 кв. км.
Половая структура населения. Во всем мире число женщин преобладает над числом мужчин. Это соотношение в целом составляет 52 к 48, но каждый год число мужчин неуклонно растет, хотя диспропорция остается. В России на 54 женщины приходится 46 мужчин, и эта половая диспропорция уже достаточно долго является одной из самых высоких в мире. В Китае, например, в когорте детского населения до 7 лет на каждых 5 мальчиков приходится только 1 девочка. И, учитывая высочайшую плотность населения Китая, уже сейчас можно предположить активную эмиграцию мужского населения через 15—20 лет в соседние регионы, где высока доля женского населения, в целях реализации репродуктивных установок, а проще говоря, в поисках «рынка невест».
Огромное значение для социально-экономических прогнозов имеет возрастная структура населения. Возрастной состав населения предопределяет важные, с экономической точки зрения, показатели демографической нагрузки, то есть соотношение численностей населения в рабочем и нерабочих (детском и пожилом) возрасте. Деление на три возрастные группы – 0-14, 15-49, 50 лет и старше – всегда условно, но все же дает довольно ясное представление о воспроизводстве населения.
Различают следующие типы воспроизводства населения: прогрессивный, стационарный и регрессивный. Прогрессивным считается тип воспроизводства населения, в котором доля детей в возрасте 0-14 лет превышает долю населения в возрасте 50 лет и старше. Стационарным называется тип, при котором доля детей равна доле лиц в возрасте 50 лет и старше. Регрессивным типом принято считать население, в котором доля лиц в возрасте 50 лет и старше превышает долю детского населения. Прогрессивный тип воспроизводства населения обеспечивает увеличение численности населения, а регрессивный угрожает нации депопуляцией. Численность населения в трудоспособном возрасте в России составила, по данным переписи 2021 года, 74,3 млн. человек (или 52,4%), моложе трудоспособного возраста – 21,4 млн. человек (15,1%) и старше трудоспособного возраста 46,2 млн. человек (32,5%).
Динамика – изменение численности населения под влиянием механического и естественного движения населения. Механическое движение населения формируется под влиянием миграционных процессов. Миграция населения— это перемещение людей, связанное, как правило, со сменой места жительства.Миграция подразделяется на безвозвратную, то есть со сменой постоянного места жительства; временную — переселение на достаточно длительный, но ограниченный срок; сезонную – перемещение в определенные периоды года; маятниковую – регулярные поездки к месту работы или учебы за пределы своего населенного пункта. Кроме того, различают внешнюю миграцию, то есть миграцию за пределы своей страны, и внутреннюю — перемещение внутри страны. К внешней миграции относятся эмиграция — выезд граждан из своей страны в другую страну на постоянное место жительства или длительный срок и иммиграция – въезд из другой страны в данную. К внутренней миграции относятся межрайонные переселения, а также переселение из села в город как важная составная часть процесса урбанизации.
Урбанизация — это процесс повышения роли городов в развитии общества.Предпосылками урбанизации являются рост в городах индустрии, развитие их культурных и политических функций. Для урбанизации характерными являются приток в города сельского населения и возрастающее маятниковое, движение населения из сел окружения и ближайших мелких городов в крупные города (на работу, по культурно-бытовым, материальным причинам и пр.). В течение прошедших двух столетий для всего населения мира был характерен интенсивный процесс урбанизации. Так, если в начале XIX века в городах мира проживало лишь 3 % населения земного шара, то к 1900 году их доля увеличилась до 13,6%, а к 1950 году — до 29,2%. В начале XXI века в городах проживает более половины населения мира, а в экономически развитых странах — более 80%.
В настоящее время в мире около 150 млн. человек живёт за пределами исторической родины. В Германии, например, иностранцы составляют 7,4 млн. человек, во Франции — 4,3 млн. (из 61 млн. жителей), из 8,8 млн. жителей Швеции почти каждый пятый (1,7 млн.) является иммигрантом или его ребенком.
Изучение миграционных процессов имеет большое значение для органов практического здравоохранения, а именно:
• процесс урбанизации изменяет экологическую обстановку, требует пересмотра необходимых объемов медицинской помощи, изменения сети медицинских учреждений, изменяет структуру, уровень заболеваемости и смертности населения, влияет на эпидемическую обстановку региона, способствует росту внебрачной рождаемости;
• маятниковая миграция увеличивает число контактов, способствующих распространению инфекционных заболеваний, ведет к росту стрессовых ситуаций, травматизма;
• сезонная миграция ведет к неравномерной сезонной нагрузке учреждений здравоохранения.
Показатели здоровья мигрантов существенно отличаются от показателей здоровья коренного населения.
Естественное движение населения
В основе естественного движения населения (процесс воспроизводства населения) лежит взаимодействие между показателями рождаемости, смертности и естественного прироста населения.Рождаемость – процесс возобновления новых поколений, и в человеческом обществе она детерминирована не только биологическими, но и социально-экономическими процессами, условиями быта, жизни, традициями, религиозными установками. Показатель рождаемости является важнейшим критерием жизнеспособности и воспроизводства населения. Рождаемость – это важнейшая составная часть естественного движения населения. За последние годы отмечается снижение уровня рождаемости во всех экономически развитых странах, что влечет за собой целый ряд нежелательных последствий: нарастание дефицита трудовых ресурсов, снижение темпа роста численности населения, изменение его возрастной структуры (постарение населения и уменьшение доли женщин фертильного возраста), увеличение количества семей, имеющих одного ребенка, и т. д.

Как статистический показатель рождаемость определяется отношением числа родившихся живыми в данном году к среднегодовой численности населения, умноженным на 1000. В областях, где коэффициент рождаемости составляет 8—10‰, преобладают однодетные семьи. В девяностые годы двадцатого века в России отмечалось резкое снижение рождаемости, уровень которой составлял 8—9‰ (в Ставропольском крае — 10‰). Начиная с 2005 года, рождаемость начала медленно повышаться, достигнув в 2021 году 13,2‰. В Европейских странах уровень рождаемости низкий — 9—12‰, в странах Юго-Восточной Азии высокий — более 25‰. Для углубленной характеристики рождаемости необходимо знать показатели общей и повозрастной плодовитости (фертильности). Показатель фертильности определяется отношением числа родившихся живыми к числу женщин детородного возраста (15—49 лет), умноженным на 1000. В России этот показатель составляет 58,8 на 1000 женщин фертильного возраста. Повозрастные показатели рождаемости (плодовитости) определяются отношением числа родившихся живыми детей у женщин различных возрастных групп (15—19, 20—24, 25—29 лет и т. д.) к числу женщин соответствующей возрастной группы, умноженным на 1000. Коэффициент суммарной плодовитости — число детей, рожденных в среднем одной женщиной за весь репродуктивный период ее жизни; брутто-коэффициент, или валовый показатель воспроизводства, показывающий число девочек, рожденных в среднем одной женщиной за весь репродуктивный период ее жизни; нетто-коэффициент, или очищенный показатель воспроизводства (число девочек, рожденных в среднем одной женщиной за весь репродуктивный период ее жизни и доживших до возраста, в котором была женщина при рождении этих девочек). Если нетто-коэффициент равен 1, брутто-коэффициент — 1,22, суммарная плодовитость — 2,2, то воспроизводство населения оценивают как стационарное. Показатели, превышающие данный уровень, характеризуют расширенное воспроизводство, а показатели ниже данного уровня — суженное воспроизводство.Среди факторов, оказывающих влияние на рождаемость, можно выделить: общественное положение женщин, их занятость в производстве, уровень материальной обеспеченности, культурный уровень, жилищные условия, пенсионное обеспечение, национальные особенности, психологические и религиозные факторы, демографическую политику государства.
Смертность населения относится к важнейшим демографическим показателям, характеризующим санитарное состояние населения. Врачебная регистрация причин смерти является ответственной функцией врача. В нашей стране в городах введена обязательная регистрация причин смерти. Врачебное свидетельство о смерти является юридическим и медицинским документом, удостоверяющим факт и причину смерти. Достоверность информации о причинах смерти населения зависит от качества заполнения врачебного свидетельства о смерти. Смертность как частоту случаев смерти среди населения изучают с помощью системы коэффициентов. Общее представление о частоте смертей дает общий коэффициент смертности: отношение числа умерших за год к среднегодовой численности населения, умноженное на 1000.

Общий показатель смертности в России составлял в начале двадцать первого века 15-16 на 1000, в Ставропольском крае —14 на 1000 человек населения. В 2021 году уровень общей смертности в РФ снизился до 13‰. Оценивается общий коэффициент смертности по схеме, в которой уровень смертности от 11 до 15‰ – считается средним, 10 ‰ и менее – низким, 16‰ и более – высоким. Анализ динамики смертности населения России показывает, что, начиная с 1990 года, уровень смертности сохранял тенденцию к росту вплоть до 2005 года. В последующем уровень общей смертности несколько снизился.
Уровень смертности во многом определяется возрастно-половой структурой населения, уровнем образования и благосостояния населения. В годы экономических кризисов, народных бедствий, войн уровень смертности значительно повышается. Уровень смертности значительно колеблется в разных странах мира.
Структура причин смертности.Наиболее характерной чертой двадцатого века является резкое снижение смертности от инфекционных болезней и увеличение доли хронических заболеваний в структуре причин общей смертности. Так, если в начале двадцатого века инфекционные заболевания были одной из ведущих причин смерти, то в последнее десятилетие их удельный вес составил менее 1%. В развивающихся странах инфекционные заболевания также стали играть меньшую роль в структуре смертности, однако их удельный вес еще велик – до 20%.
На первом месте в структуре причин смертности в России в настоящее время находятся болезни системы кровообращения (53,2%), на втором – злокачественные новообразования (15,3%), на третьем месте – внешние причины, в том числе травмы и отравления (7,8%), четвертое и пятое место делят болезни органов пищеварения и болезни органов дыхания (4,7 и 3,8%). Только на долю этих классов заболеваний приходится около 85% всех причин смертности населения Российской Федерации. В структуре смертности мужчин, по сравнению с женщинами, больший удельный вес принадлежит несчастным случаям, травмам и отравлениям, болезням органов дыхания. У женщин больший удельный вес занимают болезни системы кровообращения.
Неиспользованные резервы снижения смертности – излечимые болезни, ишемическая болезнь сердца, туберкулез и предупреждаемые болезни. С точки зрения возможностей влияния на уровень смертности – все причины смерти можно разделить на группы: причины, смертность от которых до определенного возраста может быть предотвращена самой системой здравоохранения (излечимые болезни), и смертность от которых может быть предотвращена на основе мер социальной политики при участии системы здравоохранения (предупреждаемые причины). К излечимым болезням примыкают выделенные в самостоятельные группы ишемическая болезнь сердца (ИБС) и туберкулез, включая его отдаленные последствия.
В число излечимых болезней входят большинство детских инфекций и многие острые инфекции, ряд новообразований, включая лейкемию, сахарный диабет и некоторые другие болезни эндокринной системы, все болезни органов дыхания, аппендицит, грыжа брюшной полости и некоторые другие болезни органов пищеварения, нефрит, врожденные аномалии сердца. К числу предупреждаемых причин смертности относятся злокачественные новообразования трахеи, бронхов и легких (до 15 лет не встречаются), случайные отравления алкоголем, дорожно-транспортный травматизм, СПИД.
При анализе коэффициентов смертности, наряду с общим, рассчитывают специальные коэффициенты с учетом возраста, пола, профессии и т. д. Вычисление специальных показателей смертности производится как отношение числа умерших определенного пола (возраста, профессии) за год к среднегодовой численности населения этого же пола (возраста, профессии), умноженное на 1000. Смертность мужчин выше во всех возрастных группах. Для углубленного изучения смертности и оценки воспроизводства населения наиболее совершенным приемом является построение таблиц смертности. Таблицы смертности — это система взаимосвязанных показателей, характеризующих порядок вымирания населения при данном уровне смертности в отдельных возрастных группах. Они показывают, как число одновременно родившихся, условно принятое на 10000 или 100000, постепенно уменьшается с увеличением возраста под влиянием смертности. Исходными данными для составления таблиц смертности являются: численность населения с учетом возраста, местожительства и пола на год составления таблицы, данные о смертности в соответствии с возрастом, полом и местожительством за 2 года (год составления таблицы и предыдущий), данные о рождаемости за 3 предыдущих года.Показатель младенческой смертности рассматривается как оперативный критерий оценки санитарного благополучия населения, уровня и качества медико-социальной помощи, эффективности работы акушерской и педиатрической службы. Регистрация умерших детей осуществляется на основании врачебного свидетельства о смерти и свидетельства о перинатальной смерти. Важное условие сопоставимости показателей детской смертности – унификация понятий “живорожденный”, “мертворожденный”, “плод” (поздний аборт).В России за критерий жизнеспособности плода (новорожденного) принимается срок беременности 22 недели и более, масса тела – 500 г и более. Критерии живорождения: внутриутробное легочное дыхание, сердцебиение, пульсация крупных сосудов, сокращение отдельных групп мышц. Показатель младенческой смертности вычисляют по формуле Ратса.
Младенческая смертность =
В настоящее время младенческая смертность в России в 1,5—2 раза выше, чем в ряде экономически развитых стран, и составляет 8,2 на 1000 родившихся живыми. Уровни смертности в разные периоды 1-го года жизни ребенка резко различаются. Так, смертность максимальна в 1-е сутки после рождения, в 1-ю неделю жизни, затем она постепенно снижается к первому месяцу, полугодию, году жизни. Для оценки уровня смертности в различные периоды первого года жизни ребенка рассчитывают такие показатели как: –
ранняя неонатальная смертность
(отношение числа детей, умерших в первые 7 суток (168 часов) жизни в данном году, к числу родившихся живыми в данном году, умноженное на 1000), в России — 4,6‰; —
поздняя неонатальная смертность
(отношение числа детей, умерших на 2 – 4-й неделе жизни в данном году, к числу родившихся живыми в данном году, умноженное на 1000); —
неонатальная смертность
(отношение числа детей, умерших в первые 28 дней жизни в данном году, к числу родившихся живыми в данном году, умноженное на 1000), в России —7‰; —
постнеонатальная смертность
(отношение числа детей, умерших в возрасте от 29 дней до 1 года, к разнице между числом родившихся живыми и числом умерших в первые 28 дней жизни, умноженное на 1000), в России — 4‰.
Перинатальным периодом
считается промежуток времени, начиная с 22-й полной недели беременности (154 дня внутриутробной жизни плода) и кончая 7-м днем жизни новорожденного (168 часов после рождения). В свою очередь, он подразделяется на антенатальный (внутриутробный), интранатальный (период родов) и постнатальный (1-я неделя жизни). Антенатальная и интранатальная смертность в сумме дают мертворождаемость.
Показатель перинатальной смертности
вычисляется как отношение суммы числа мертворожденных и числа детей, умерших в первые 168 часов жизни, к числу родившихся живыми и мертвыми, умноженное на 1000. Факторами, влияющими на антенатальную и интранатальную гибель плода, являются: поздние токсикозы беременных, болезни матери (грипп, сердечно-сосудистые заболевания и др.), патология плаценты, пуповины, преждевременное отхождение околоплодных вод, слабость родовой деятельности и др. Основными причинами перинатальной смертности следует считать внутриутробную гипоксию и асфиксию при родах (46,5%), синдром респираторного расстройства (18,0%), врожденные аномалии (14,4%), инфекционные болезни, специфичные для перинатального периода (12,3%), гемолитическую болезнь (3,2%).Основными причинами младенческой смертности являются отдельные состояния, возникшие в перинатальном периоде (в том числе родовые травмы, асфиксия и респираторные состояния новорожденных), врожденные аномалии, болезни органов дыхания, инфекционные и паразитарные болезни, травмы и отравления и другие.
Наиболее информативным показателем, характеризующим состояние и перспективы воспроизводства населения в стране, является коэффициент естественного прироста, который рассчитывается как разность между общим показателем рождаемости и общим показателем смертности и не зависит от направления и интенсивности миграционного обмена.
Естественный прирост населения = Общий показатель рождаемости минус общий показатель смертности
Положительный коэффициент естественного прироста означает, что население рассматриваемой территории увеличивается, а отрицательный – что население территории уменьшается. Отрицательный естественный прирост всегда свидетельствует о явном неблагополучии в обществе. Негативные тенденции воспроизводства, сохраняющиеся достаточно продолжительное время, обычно приводят к депопуляции – сокращению численности населения страны и ее отдельных территорий, что в настоящее время является нежелательной реальностью для России. Естественная убыль населения России началась в 1992 году и за период между переписями 1989 и 2002 гг. составила около 7,4 млн. человек, при этом наблюдается депопуляция основного этноса страны – русских, что является не только этнической, но и общегосударственной политической, социальной и экономической проблемой.
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
Вычислите показатели естественного движения населения:
1.Показатель рождаемости, общей смертности, естественного прироста населения.
2.Показатель младенческой смертности, смертности новорожденных, перинатальной смертности, ранней неонатальной смертности и мертворождаемости.
3.Определить структуру причин младенческой смертности.
4.Дать оценку демографических показателей на основании принятых средних уровней.
5.Определить тип воспроизводства населения, сложившийся в населенном пункте.
6.Сравнить вычисленные демографические показатели за отчётный год с соответствующими показателями предыдущего года.
7.Графически изобразить уровень рождаемости, общей смертности, естественного прироста населения, структуру причин младенческой смертности.
Задача 1
§
Число случаев ВН по поводу одной нозологической формы заболевания ×100
Число всех случаев заболеваний с временной утратой трудоспособности
При анализе ЗВУТ определяется структура временной нетрудоспособности в случаях и днях (первое место занимают заболевания острыми респираторными инфекциями, далее – гипертоническая болезнь, болезни костно-мышечной системы, инфекции кожи, болезни органов пищеварения и др.). Все показатели заболеваемости оцениваются по нозологическим формам (в случаях и в днях на 100 работающих) и в динамике за ряд лет. При углубленной методике изучения заболеваемости с ВУТ полицевым методом на каждого работающего заполняется лицевая, или персональная, карта. Единицей наблюдения при этой методике является работающий. При полицевом учете заболеваемости оцениваются: индекс здоровья; кратность заболеваний (1, 2, 3 раза); удельный вес часто болеющих (4 раза и более в году) и длительно болеющих (более 30 дней).
Показатели госпитальной заболеваемости
Заболеваемость госпитализированных больных – это учет лиц, лечившихся в стационаре в течение года. Сведения о госпитализированной заболеваемости позволяют судить о своевременности госпитализации, продолжительности и исходе лечения, совпадении или расхождении диагнозов, объеме оказанной медицинской помощи и др. Данные о госпитализированной заболеваемости учитываются при планировании коечного фонда, определении потребности в различных видах стационарной помощи. Единицей наблюдения при изучении госпитализированной заболеваемости является каждый случай госпитализации. Учетной статистической формой служит карта выбывшего из стационара. Общий уровень госпитализации составляет около 150 случаев на 1000 человек. В структуре госпитализированных больных основную долю составляют больные заболеваниями органов кровообращения, пищеварения, хроническими заболеваниями органов дыхания, больные с травмами.
Заболеваемость, выявляемая активно при медицинских осмотрах
Количество заболеваний, выявляемых в ходе обращаемости населения за медицинской помощью, велико, но оно значительно ниже истинного числа заболеваний, которыми страдало население в течение года. Заболеваемость можно сравнить с айсбергом, надводную часть которого составляют болезни, по поводу которых население обращается в медицинские учреждения, а подводную – те, которые остаются неизвестными для медицинских работников. Поэтому для более полной оценки общественного здоровья показатели по данным обращаемости необходимо дополнять данными, полученными в результате проводимых медицинских осмотров. Лучшим способом проведения массового медицинского осмотра, с точки зрения его качества, является проведение его бригадой специалистов. Однако такие осмотры связаны с необходимостью привлечения значительных кадровых, финансовых, материальных ресурсов.
Поэтому стремление охватить медицинскими осмотрами как можно большую часть населения с привлечением ограниченного объема ресурсов обусловило разработку и внедрение различных организационных форм обследования с использованием многообразных тестов. Эти организационные формы носят общее название «скрининг».
Скрининг — это массовое обследование населения и выявление лиц с заболеваниями или с начальными признаками заболеваний. Основная цель скрининга — провести первичный отбор лиц, требующих углубленного обследования, консультации узких специалистов, формирования групп повышенного риска заболевания определенной патологией.
Заболеваемость, выявляемая при профилактических медицинских осмотрах, называется патологической пораженностью. Периодические и массовые медицинские осмотры позволяют выявить ранее не известные хронические заболевания, по поводу которых население не обращается активно в медицинские учреждения. Учету подлежат случаи начальных (скрытых) проявлений тех или иных болезней. Достоинством метода активных медицинских осмотров является также уточнение диагностики некоторых хронических заболеваний и патологических отклонений. Основной учетный документ при изучении этого вида заболеваемости – «Список лиц, подлежащих целевому медицинскому осмотру». Анализ изучения заболеваемости по данным медицинских осмотров проводится по показателям частоты выявленных при профилактических осмотрах заболеваний (отношение числа выявленных заболеваний к числу обследованных, умноженное на 1000). При этом анализе производится и расчет структуры выявленной патологии, определяется индекс здоровья. При выборе основного диагноза следует руководствоваться “Международной классификацией болезней и проблем, связанных со здоровьем” (10-й пересмотр, 1995 г.). При диагностике и шифровке заболеваемости предпочтение следует отдавать: 1) основной болезни, а не осложнению; 2) более тяжелой и смертельной болезни; 3) инфекционным, а не неинфекционным заболеваниям; 4) острой форме заболевания, а не хронической; 5) специфическому заболеванию, связанному с определенными условиями труда и быта.
Заболеваемость по данным о причинах смерти
Источники информации, основные показателиИсточником информации о заболеваемости и причинах смерти является врачебное свидетельство о смерти. В нем должны быть указаны непосредственная причина смерти и заболевание, вызвавшее или обусловившее непосредственную причину смерти, то есть основное заболевание. Кроме того, указываются все сопутствующие заболевания, имевшиеся у больного. В загсах на основании врачебного свидетельства о смерти составляется “Акт о смерти”. Эти акты ежемесячно направляются в статистическое управление края (области), где составляются отчеты, и проводится анализ причин смертности.Исследования частоты заболеваний, способствовавших смертельному исходу, позволяют изучить летальность при различных заболеваниях (число умерших среди 100 заболевших). При анализе заболеваемости по данным о причинах смерти используются общие и специальные показатели: общие показатели – число умерших за отчетный год на 1000 жителей; специальные показатели: а) показатель смертности в зависимости от заболевания – число умерших от того или иного заболевания на 1000 жителей; б) показатель смертности в зависимости от пола (возраста, профессии и др.) – число умерших за год лиц определенного пола (возраста, профессии и др.) на 1000 жителей этой группы; в) показатель структуры причин смертности – процентное отношение числа умерших от определенных заболеваний к общему числу умерших. В структуре общей смертности населения первое место занимают болезни органов кровообращения. Основными факторами риска смертности и летальности при этих заболеваниях являются гиподинамия, особенно в условиях крупного города, избыточная масса тела, наличие вредных привычек (курение и употребление алкогольных напитков, стрессовые ситуации и пр.). На втором месте стоят онкологические заболевания, которые обусловлены воздействием таких факторов риска, как загрязнение окружающей среды вредными химическими соединениями, радиация, курение, и пр. Третье место в структуре общей смертности занимают травмы и четвертое – хронические неспецифические заболевания легких.ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ:
Задание №1.
По данным годового отчета рассчитать показатели заболеваемости населения, проживающего в районе обслуживания данного лечебно-профилактического учреждения
Методика расчета показателей
:
1.Уровень первичной заболеваемости (собственно заболеваемость):
Число вновь возникших заболеваний × 1000
Среднегодовая численность населения
Средний уровень собственно заболеваемости в РФ взрослого населения – 700‰ , подростков –900‰ , детей – 1200‰ .
2. Уровень болезненности (распространенность):
Число всех зарегистрированных заболеваний у населения за год × 1000
Среднегодовая численность населения
Средний уровень болезненности в РФ взрослого населения – 1200‰, подростков – 1500‰, детей – 1900‰.
3. Структура первичной заболеваемости населения в данном году:

Задание №2. Вычислите следующие показатели заболеваемости с временной утратой трудоспособности на промышленном предприятии:
1. Число случаев заболеваний на 100 работающих.2. Число больных лиц на 100 работающих (круглогодовых).3. Число дней ВН, приходящиеся на 100 работающих в год.4. Среднюю продолжительность одного случая временной нетрудоспособности.5. Кратность заболеваний.6. Структуру заболеваемости с ВН.Сопоставьте полученные данные со средними по Российской Федерации (табл.11). Дайте заключение
Задача 1
На кондитерской фабрике среднегодовое число работающих составило 950 человек. Круглогодовое число работающих – 835 человек. Число больных лиц – 650. Число случаев утраты трудоспособности в отчетном году достигло 690, а число дней временной утраты трудоспособности – 8965, в том числе по поводу острых респираторных заболеваний – 1832 дня, болезней органов пищеварения – 1095 дней, болезней системы кровообращения– 855 дней, болезней костно-мышечной системы – 557 дней, травм -143 дня.
Задача 2
На машиностроительном предприятии среднегодовое число работающих составило 1770 человек. Круглогодовое число работающих – 1650 человек. Число больных лиц – 1240. Число случаев утраты трудоспособности в отчетном году достигло 1360, а число дней временной утраты трудоспособности – 17825, в том числе по поводу острых респираторных заболеваний – 2842 дня, болезней органов пищеварения – 830 дней, болезней системы кровообращения– 1190 дней, болезней костно-мышечной системы – 1175 дней, травм -1543 дня.
Задача 3
На предприятии электронной промышленности среднегодовое число работающих составило 1300 человек. Круглогодовое число работающих – 1150 человек. Число больных лиц – 965. Число случаев утраты трудоспособности в отчетном году достигло 1070, а число дней временной утраты трудоспособности – 12200, в том числе по поводу острых респираторных заболеваний – 2950 дня, болезней органов пищеварения – 930 дней, болезней системы кровообращения– 980 дней, болезней костно-мышечной системы – 707 дней, травм -233 дня.
Задача 4
На обувной фабрике среднегодовое число работающих составило 620 человек. Круглогодовое число работающих – 575 человек. Число больных лиц – 550. Число случаев утраты трудоспособности в отчетном году достигло 590, а число дней временной утраты трудоспособности 2985, в том числе по поводу острых респираторных заболеваний 684 дня, болезней органов пищеварения – 320 дней, болезней системы кровообращения – 440 дней, болезней костно-мышечной системы – 317 дней, травм -413 дня.
Задача 5
На химическом предприятии среднегодовое число работающих составило 1200 человек. Круглогодовое число работающих – 1100 человек. Число больных лиц – 960. Число случаев утраты трудоспособности в отчетном году достигло 1170, а число дней временной утраты трудоспособности – 11500, в том числе по поводу острых респираторных заболеваний – 2954 дня, болезней органов пищеварения – 2705 дней, болезней системы кровообращения – 1189 дней, болезней костно-мышечной системы – 730 дней, болезни кожи и подкожной клетчатки – 580 дней.
Задача 6
На ткацкой фабрике среднегодовое число работающих составило 1470 человек. Круглогодовое число работающих -1250 человек. Число больных лиц – 950. Число случаев утраты трудоспособности в отчетном году достигло 1280, а число дней временной утраты трудоспособности – 9910, в том числе по поводу острых респираторных заболеваний – 2062 дня, болезней органов пищеварения – 808 дней, болезней системы кровообращения – 915 дней, болезней костно-мышечной системы – 770 дней, травм -334 дня.
Задача 7
На консервном заводе среднегодовое число работающих составило 517 человек. Круглогодовое число работающих – 450 человек. Число больных лиц – 340. Число случаев утраты трудоспособности в отчетном году достигло 390, а число дней временной утраты трудоспособности – 3910, в том числе по поводу острых респираторных заболеваний – 1062 дня, болезней органов пищеварения – 158 дней, болезней системы кровообращения – 365 дней, болезней костно-мышечной системы – 210дней, травм – 402 дня.
Задача 8
На мясокомбинате среднегодовое число работающих составило 915 человек. Круглогодовое число работающих – 880 человек. Число больных лиц –772. Число случаев утраты трудоспособности в отчетном году достигло 850, а число дней временной утраты трудоспособности – 6956, в том числе по поводу острых респираторных заболеваний – 1993 дня, болезней органов пищеварения – 236 дней, болезней системы кровообращения – 435 дней, болезней костно-мышечной системы – 487 дней, травм – 422 дня.
Таблица 11
Показатели временной нетрудоспособности в Российской Федерации
| Показатели | Всего | В том числе: | |||
| ОРВИ | Болезней системы кровообращения | Болезней органов пищеварения | Травмы | ||
| Число случаев ВН на 100 работающих | 69,8 | 14,8 | 4,0 | 3,6 | 6,1 |
| Число дней ВН на 100 работающих | 908,4 | 118,5 | 72,9 | 60,6 | 128,6 |
| Средняя длительность одного случая | 13,0 | 8,0 | 18,2 | 16,8 | 21,1 |
Рекомендуемая литература:
· Медик В.А., Юрьев В.К.Общественное здоровье и здравоохранение. Учебник для вузов: – М: ГЭОТАР – Медиа. – 2021, – 608 с.
· Медик В.А.Общественное здоровье и здравоохранение: Руководство к практическим занятиям: – М: ГЭОТАР – Медиа. – 2021, – 400 с.
· Щепин О.П., Медик В.А.Общественное здоровье и здравоохранение. Учебник для вузов: – М., 2021, – 592 с.
· Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
· Ю.П. Лисицын. Общественное здоровье и здравоохранение. Учебник для вузов. М., 2002. – с. 217 – 255.
· В.К. Юрьев, Г.И. Куценко.Общественное здоровье и здравоохранение. С.-П., 2000. –с. 69 – 89.
· Общественное здоровье и здравоохранение. Под ред. В.А. Миняева, Н.И. Вишнякова. М. «МЕДпресс-информ», 2002. – с. 51 – 56.
Приложения:
Способы расчета числа наблюдений (n), необходимых для получения достоверных средних и относительных величин при планировании эксперимента.
Репрезентативность выборочной статистической совокупности обеспечивается предварительным расчетом необходимого объема выборки и применением специальных методик отбора единиц наблюдения.
При неизвестной величине генеральной совокупности величину выборки, гарантирующую репрезентативные результаты, если результат выражается в относительных показателях, определяют по формуле:
n =  , где р — величина показателя изучаемого признака; q = (100 – p); t — доверительный коэффициент, показывающий, какова вероятность того, что размеры показателя не будут выходить за границы предельной ошибки (обычно берется t=2, что обеспечивает 95% вероятность безошибочного прогноза);
, где р — величина показателя изучаемого признака; q = (100 – p); t — доверительный коэффициент, показывающий, какова вероятность того, что размеры показателя не будут выходить за границы предельной ошибки (обычно берется t=2, что обеспечивает 95% вероятность безошибочного прогноза);  — предельная ошибка показателя.
— предельная ошибка показателя.
Например: одним из показателей, характеризующих здоровье рабочих промышленных предприятий, является процент не болевших в течение года работников. Предположим, что для промышленной отрасли, к которой относится обследуемое предприятие, этот показатель равен 25%. Предельная ошибка, которую можно допустить, чтобы разброс значений показателя не превышал разумные границы, 5%. При этом показатель может принимать значения 25% ±5%, или от 20% до 30%. Допуская t = 2, получаем
n =  =300 рабочих.
=300 рабочих.
В том случае, если показатель — средняя величина, то число наблюдений можно установить по формуле: n =  ,
,
где  — показатель вариабельности признака (среднеквадратическое отклонение), который можно получить из предыдущих исследований либо на основании пробных (пилотажных) исследований.
— показатель вариабельности признака (среднеквадратическое отклонение), который можно получить из предыдущих исследований либо на основании пробных (пилотажных) исследований.
При условии известной генеральной совокупности для определения необходимого размера случайной выборки в случае использования относительных величин применяется формула:
n = 
Для средних величин используется формула:
n =  , где N- численность генеральной совокупности.
, где N- численность генеральной совокупности.
В целом, число наблюдений, необходимое для получения репрезентативных данных, изменяется обратно пропорционально квадрату допустимой ошибки.
Таблица 1







