Реферат – Комплексные числа и их свойства

Введение

Рассмотрев тему «комплексные числа» на занятиях
высшей математики мы заинтересовались данной темой и решили углубить свои
познания в этой области.

Большое значение комплексных чисел в математике
и её приложениях широко известно. Их изучение имеет самостоятельный интерес.
Алгебру комплексных чисел можно успешно использовать в элементарной геометрии,
тригонометрии, теории геометрических преобразований, а также в электротехнике и
различных задачах с механическим и физическим содержанием.

История комплексных чисел

Древнегреческие математики считали
“настоящими” только натуральные числа. Постепенно складывалось
представление о бесконечности множества натуральных чисел.

В III
веке Архимед разработал систему обозначения вплоть до такого громадного как

Наряду с натуральными числами применяли дроби –
числа, составленные из целого числа долей единицы. В практических расчетах
дроби применялись за две тысячи лет до н. э. в древнем Египте и древнем
Вавилоне. Долгое время полагали, что результат измерения всегда выражается или
в виде натурального числа, или в виде отношения таких чисел, то есть дроби.
Древнегреческий философ и математик Пифагор учил, что “… элементы чисел
являются элементами всех вещей и весь мир в челом является гармонией и числом.
Сильнейший удар по этому взгляду был нанесен открытием, сделанным одним из
пифагорейцев. Он доказал, что диагональ квадрата несоизмерима со стороной.
Отсюда следует, что натуральных чисел и дробей недостаточно, для того чтобы выразить
длину диагонали квадрата со стороной 1. Есть основание утверждать, что именно с
этого открытия начинается эра теоретической математики: открыть существование
несоизмеримых величин с помощью опыта, не прибегая к абстрактному рассуждению,
было невозможно.

Следующим важным этапом в развитии понятия о
числе было введение отрицательных чисел – это было сделано китайскими
математиками за два века до н. э. Отрицательные числа применяли в III
веке древнегреческий математик Диофант, знавший уже правила действия над ними,
а в VII веке эти
числа уже подробно изучили индийские ученые, которые сравнивали такие числа с
долгом. С помощью отрицательных чисел можно было единым образом описывать
изменения величин. Уже в VIII
веке было установлено, что квадратный корень из положительного числа имеет два
значения – положительное и отрицательное, а из отрицательных чисел квадратный
корень извлекать нельзя: нет такого числа ,
чтобы .

В XVI
веке в связи с изучением кубических уравнений оказалось необходимым извлекать
квадратные корни из отрицательных чисел. В формуле для решения кубических
уравнений вида  кубические и
квадратные корни

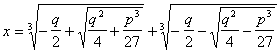
Эта формула безотказно действует в случае, когда
уравнение имеет один действительный корень (),
а если оно имеет три действительных корня (),
то под знаком квадратного корня оказывалось отрицательное число. Получалось,
что путь к этим корням ведет через невозможную операцию извлечения квадратного
корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й
степени, математики усиленно искали формулу для решения уравнения 5-й степени.
Но Руффини (Италия) на рубеже XVIII
и XIX веков доказал, что
буквенное уравнение пятой степени  нельзя
решить алгебраически; точнее: нельзя выразить его корень через буквенные
величины a, b,
c, d,
e с помощью шести
алгебраических действий (сложение, вычитание, умножение, деление, возведение в
степень, извлечение корня).

В 1830 году Галуа (Франция) доказал, что никакое
общее уравнение, степень которого больше чем 4, нельзя решить алгебраически.
Тем не менее всякое уравнение n-й степени имеет (если рассматривать и
комплексные числа) n корней
(среди которых могут быть и равные). В этом математики были убеждены еще в XVII
веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже
XVIII и XIX
веков
упомянутая теорема была доказана Гауссом.

Итальянский алгебраист Дж. Кардано в 1545 г.
предложил ввести числа новой природы. Он показал, что система уравнений ,
не имеющая решений во множестве действительных чисел, имеет решения вида ,
,
нужно только условиться действовать над такими выражениями по правилам обычной
алгебры и считать что . Кардано называл
такие величины “чисто отрицательными” и даже “софистически
отрицательными”, считал их бесполезными и старался их не употреблять. В
самом деле, с помощью таких чисел нельзя выразить ни результат измерения
какой-нибудь величины, ни изменение какой-нибудь величины. Но уже в 1572 году
вышла книга итальянского алгебраиста Р. Бомбелли, в которой были установлены
первые правила арифметических операций над такими числами, вплоть до извлечения
из них кубических корней. Название “мнимые числа” ввел в 1637 году французский
математик и философ Р. Декарт, а в 1777 году один из крупнейших математиков XVIII
века – Л. Эйлер предложил использовать первую букву французского слова imaginaire
(мнимый) для обозначения числа  (мнимой единицы).
Этот символ вошел во всеобщее употребление благодаря К. Гауссу . Термин
“комплексные числа” так же был введен Гауссом в 1831 году. Слово
комплекс (от латинского complexus)
означает связь, сочетание, совокупность понятий, предметов, явлений и т. д.
Образующих единое целое.

В течение XVII
века продолжалось обсуждение арифметической природы мнимых чисел, возможности
дать им геометрическое обоснование.

Постепенно развивалась техника операций над
мнимыми числами. На рубеже XVII
и XVIII веков была
построена общая теория корней n-ых
степеней сначала из отрицательных, а за тем из любых комплексных чисел,
основанная на следующей формуле английского математика А. Муавра (1707)

С помощью этой формулы можно было так же вывести
формулы для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году
замечательную формулу : , которая связывала
воедино показательную функцию с тригонометрической. С помощью формулы Л. Эйлера
можно было возводить число e
в любую комплексную степень. Любопытно, например, что .
Можно находить sin
и cos от комплексных
чисел, вычислять логарифмы таких чисел, то есть строить теорию функций
комплексного переменного.

В конце XVIII
века французский математик Ж. Лагранж смог сказать, что математический анализ
уже не затрудняют мнимые величины. С помощью мнимых чисел научились выражать
решения линейных дифференциальных уравнений с постоянными коэффициентами. Такие
уравнения встречаются, например, в теории колебаний материальной точки в
сопротивляющейся среде. Еще раньше швейцарский математик Я. Бернулли применял
комплексные числа для решения интегралов.

Хотя в течение XVIII
века с помощью комплексных чисел были решены многие вопросы, в том числе и
прикладные задачи, связанные с картографией, гидродинамикой и т. д., однако еще
не было строго логического обоснования теории этих чисел. По этому французский
ученый П. Лаплас считал, что результаты, полученные с помощью мнимых чисел, –
только наведение, приобретающее характер настоящих истин лишь после
подтверждения прямыми доказательствами.

“Никто ведь не сомневается в точности
результатов, получаемых при вычислениях с мнимыми количествами, хотя они
представляют собой только алгебраические формы иероглифы нелепых
количеств” Л. Карно.

В конце XVIII
века, в начале XIX
века было получено геометрическое истолкование комплексных чисел. Датчанин К.
Вессель, француз Ж. Арган и немец К. Гаусс независимо друг от друга предложили
изобразить комплексное число  точкой  на
координатной плоскости. Позднее оказалось, что еще удобнее изображать число не
самой точкой M, а вектором ,
идущим в эту точку из начала координат.

При таком истолковании сложение и вычитание
комплексных чисел соответствуют эти же операции над векторами. Вектор  можно
задавать не только его координатами a
и b, но так же длиной r
и углом j, который он
образует с положительным направлением оси абсцисс.

При этом ,
 и
число z принимает вид ,
который называется тригонометрической формой комплексного числа. Число r
называют модулем комплексного числа z
и обозначают . Число  называют
аргументом z и обозначают ArgZ.
Заметим, что если , значение ArgZ
не определено, а при  оно определено с
точностью до кратного .

Упомянутая ранее формула Эйлера позволяет
записать число z в виде  (показательная
форма комплексного числа).

Геометрическое истолкование комплексных чисел
позволило определить многие понятия, связанные с функцией комплексного
переменного, расширило область их применения.

Стало ясно, что комплексные числа полезны во
многих вопросах, где имеют дело с величинами, которые изображаются векторами на
плоскости: при изучении течения жидкости, задач теории упругости.

После создания теории комплексных чисел возник
вопрос о существовании “гиперкомплексных” чисел – чисел с несколькими
“мнимыми” единицами.

Такую систему вида

где ,
построил в 1843 году ирландский математик У. Гамильтон, который назвал их
“кватернионами”.

Правила действия над кватернионами напоминает
правила обычной алгебры, однако их умножение не обладает свойством
коммутативности (переместительности): например, ,
а .
Гиперкомплексные числа не являются темой этого реферата, поэтому лишь упомянем
об их существовании.

Большой вклад в развитие теории функций комплексного
переменного внесли русские и советские ученые Н. И. Мусхелишвили занимался ее
применениями к упругости, М. В. Келдыш и М. А. Лаврентьев – к аэро- и
гидродинамике, Н. Н. Богомолов и В. С. Владимиров – к проблемам квантовой
теории поля.

Комплексное число имеет вид a
bi; здесь a
и b – действительные
числа , а i – число нового
рода, называемое мнимой единицей.

“Мнимые” числа составляют частный вид
комплексных чисел (когда а = 0). С другой стороны, и действительные числа
являются частным видом комплексных чисел (когда b
= 0).

Действительное число a
назовем абсциссой комплексного числа a
bi; действительное
число b – ординатой
комплексного числа a bi.
Основное свойство числа i
состоит в том, что произведение i*i
равно -1, т.е.

i2= -1

Долгое время не удавалось найти такие физические
величины, над которыми можно выполнять действия, подчинённые тем же правилам,
что и действия над комплексными числами – в частности правилу (1). Отсюда
названия: “мнимая единица”, “мнимое число” и т.п. В настоящее время известен
целый ряд таких физических величин, и комплексные числа широко применяются не
только в математике, но также и в физике и технике.

Оставим в стороне вопрос о геометрическом или
физическом смысле числа i,
потому что в разных областях науки этот смысл различен.

Правило каждого действия над комплексными
числами выводится из определения этого действия. Но определения действий над
комплексными числами не вымышлены произвольно, а установлены с таким расчетом,
чтобы согласовались с правилами действий над вещественными числами. Ведь
комплексные числа должны рассматриваться не в отрыве от действительных, а
совместно с ними.

отрезок комплексный число

Соглашение о комплексных числах

1. Действительное
число а записывается также в виде a
0i (или a
– 0i).

Примеры. Запись 3 0i
обозначает то же, что запись 3. Запись -2 0i
означает -2.

2. Комплексное
число вида 0 bi
называется “чисто мнимым”. Запись bi
обозначает то же, что 0 bi.

3. Два
комплекных a bi,
a’ b’i
считаются равными, если у них соответственно равны абсциссы и ординаты, т. е.
Если a = a’,
b = b’.

4. В
противном случае комплексные числа не равны. Это определение подсказывается
следующим соображением. Если бы могло существовать, скажем, такое равенство: 2
5i = 8 2i,
то по правилам алгебры мы имели бы i
= 2, тогда как i не должно
быть действительным числом.

Замечание. Мы еще не определили, что такое
сложение комплексных чисел. Поэтому, строго говоря, мы ещё не в праве
утверждать, что число 2 5i
есть сумма чисел 2 и 5i.
Точнее было бы сказать, что у нас есть пара действительных чисел: 2 (абсцисса)
и 5 (ордината); эти числа порождают число нового рода, условно обозначаемое 5
7i.

Сложение комплексных чисел

Определение. Суммой комплексных чисел a
bi и a’
b’i
называют комплексное число (a
a’) (b
b’)i.

Это определение подсказывается правилами
действий с обычными многочленами.

Пример 1. (-3 5i) (4 – 8i) = 1 –
3i

Пример 2. (2 0i) (7 0i) = 9
0i. Так
как запись 2 0i означает то
же, что и 2 и т. д., то наполненное действие согласуется с обычной арифметикой
(2 7=9).

Пример 3. (0 2i) (0 5i) = 0
7i, т. е. 2i 5i = 7i

Пример 4. (-2 3i)
( – 2 – 3i) = – 4

В примере 4 сумма двух комплексных чисел равна
действительному числу. Два комплексных числа a bi
и a-bi
называются сопряженными. Сумма сопряженных комплексных чисел равна
действительному числу.

Замечание. Теперь, когда действие сложения
определено, мы имеем право рассматривать комплексное число a
bi как сумму чисел a
и bi. Так, число 2 и
число 5i в сумме дают число
2 5i.

Вычитание комплексных чисел.

Оп ределение.

Разностью комплексных чисел a
bi (уменьшаемое) и a’
b’i
(вычитаемое) называется комплексное число (a
– a’) (b
– b’)i.

Пример 1. (-5 2i) – (3 – 5i) = -8
7i

Пример 2. (3 2i) – (-3 2i) = 6
0i = 6

Умножение комплексных чисел.

Определение умножения комплексных чисел
устанавливается с таким расчетом, чтобы 1) числа a
bi и a’
b’i
можно было перемножать, как алгебраические двучлены, и чтобы 2) число i
обладало свойством i 2= – 1. В
силу требования 1) произведение (a
bi)(a’
b’i)
должно равняться aa’
(ab’ ba’)i
bb’i2
, а в силу требования 2) это выражение должно равняться (aa’
– bb’) (ab’
ba’)i.
В соответствии с этим устанавливается следующее определение.

Определение. Произведением комплексных чисел a
bi и a’
b’i
называется комплексное число (aa’
– bb’) (ab’
ba’)i.

Замечание 1. Равенство i2
= -1 до установленного правила умножения комплексных чисел носило характер
требования. Теперь оно вытекает из определения. Ведь запись i
2 , т. е. i*i,
равнозначна записи (0 1*i)(0
1*i). Здесь a
= 0, b = 1, a’
= 0, b’ = 1 Имеем aa’
– bb’ = -1, ab’
ba’ = 0, так что
произведение есть -1 0i,
т. е. -1.

Замечание 2. На практике нет нужды пользоваться
формулой произведения. Можно перемножить данные числа, как двучлены, а затем
положить, что i2 = -1.

Пример 1. (1 – 2i)(3 2i) = 3 – 6i
2i – 4i 2 = 3 – 6i 2i 4 = 7 – 4i.

Пример 2. (a bi)(a – bi) = a2 b
2

Пример 2 показывает, что произведение
сопряженных комплексных чисел есть действительное и притом положительное число.

В соответсвии с определением деления
действительных чисел устанавливается следующее определение.

Опредление. Разделить комплексное число a
bi на комплексное
число a’ b’i
– значит найти такое число x
yi, которое, будучи
помножено на делитель, даст делимое.

Если делитель не равен нулю, то деление всегда
возможно, и частное единственно (доказательство смотри в замечании 2). На
практике частное удобнее всего находить следующим образом.

Пример 1. Найти частное (7 – 4i):(3
2i).

Записав дробь (7 – 4i)/(3
2i), расширяем её на
число 3 – 2i, сопряженное с 3
2i. Получим:

((7 – 4i)(3 – 2i))/((3 2i)(3 –
2i)) = (13 – 26i)/13 = 1 – 2i.

Пример 2. (-2 5i)/(-3 -4i) = ((-2
5i)(-3 – 4i))/((-3 – 4i)( -3 4i)) = (-14 -23i)/25 = -0,56 – 0.92i.

Чтобы доказать, что правая часть действительно
является частным, достаточно помножить её на a’
b’. Получим a
bi.

Геометрический смысл сложения и вычитания
комплексных чисел

Пусть векторы ОМ и ОМ’ (рис. 1) изображают
комплексные числа z= x
yi u
z’ = x’
y’i.
Из точки М проведем вектор МК, равный OM’.
Тогда вектор ОК изображает сумму данных комплексных чисел.

Построенный указанным образом вектор ОК
называется геометрической суммой векторов ОМ и ОМ’.

Итак, сумма двух комплексных чисел
представляется суммой векторов, изображающих отдельные слагаемые.

Длина стороны ОК треугольника ОМК меньше суммы и
больше разницы длин ОМ и МК. Поэтому

||z|
– |z’|| < |z
z’| < |z|
|z’|.

Рис. 1

Равенство имеет смысл только в тех случаях,
когда векторы ОМ и ОМ’ имеют одинаковые или противоположные направления. В
первом случае |OM|
|OM’| = |OK|,
т. е. |z z’|=|z|
|z’|. Во втором
случае |z z’|=||z|
– |z’||.

Геометрическая интерпретация комплексных чисел.
Длина отрезка

При заданной прямоугольной декартовой системе
координат на плоскости комплексному числу z = x iy (i2= -1) можно взаимно
однозначно поставить в соответствие точку М плоскости с координатами х, у (рис.1)

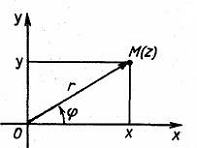
Рис. 2

.

Число z тогда называют комплексной
координатой точки М.

Поскольку множество точек евклидовой
плоскости находится во взаимно однозначном соответствии с рис. 2 множеством
комплексных чисел, то эту плоскость называют

также плоскостью комплексных чисел.
Начало О декартовой системы координат называют при этом начальной или нулевой
точкой плоскости комплексных чисел.

При у=0 число z
действительное. Действительные числа изображаются точками оси х, поэтому она
называется действительной осью. При х=0 число z чисто
мнимое: z=iy. Мнимые
числа изображаются точками оси у, поэтому она называется мнимой осью. Нуль – одновременно
действительное и чисто мнимое число.

Paccтoяниe от начала О
плоскости до точки М(z) называется модулем комплексного числа z и
обозначается |z| или r

|z| = r = |OM| = .

Если  – ориентированный угол,
образованный вектором с осью х, то
по определению функции синуса и косинуса

откуда  и поэтому .

Такое представление комплексного
числа z называется его тригонометрической формой. Исходное представление z=x iy называют
алгебраической формой этого числа. При тригонометрическом представлении угол  называют
аргументом комплексного числа и обозначают еще через arg z:

.

Если дано комплексное число z=x iy, то число  называется
комплексно-сопряженным (или просто сопряженным) этому числу z. Тогда, очевидно,
и число z сопряжено числу . Точки М(z)
и  симметричны
относительно оси х (рис.2).

Из равенства следует y=0 и
обратно. Это значит, что число, равное своему сопряженному, является
действительным и обратно.

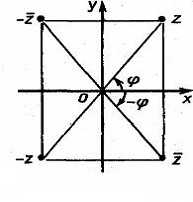
Рис. 3

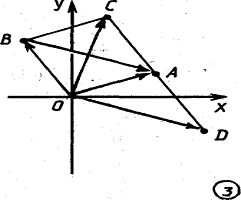
Рис. 4

Точки с комплексными координатами z и -z
симметричны относительно начальной точки О (рис.3). Точки с комплексными
координатами z и  симметричны
относительно оси у. Из равенства z= вытекает x=0 и
обратно. Поэтому условие z= является критерием чисто мнимого
числа. Для любого числа z, очевидно, |z| = || = |-z| = ||.

Сумма и произведение двух
сопряженных комплексных чисел являются действительными числами

Число, сопряженное с суммой,
произведением или же частным комплексных чисел, есть соответственно сумма,
произведение или же частное чисел, сопряженных данным комплексным числам:

Эти равенства можно легко проверить,
пользуясь формулами для операций над комплексными числами. Каждой точке М(z)
плоскости – взаимно однозначно соответствует вектор . Поэтому
комплексные числа можно интерпретировать векторами, приложенными к точке O.
Сложению и вычитанию комплексных чисел отвечает сложение и вычитание
соответствующих им векторов. Именно если а и b – комплексные координаты точек A
и В соответственно, то число с=а b является координатой точки С, такой, что  (рис.4).
Комплексному числу d=a-b соответствует такая точка D, что .

Расстояние между точками А и В равно
:

|АВ| = |а-b|

Так как |z|2= z, то

|AB|2=(a-b)()

Уравнение z= r2 определяет
окружность с центром О радиуса r. Отношение , в котором
точка С делит данный отрезок АВ, выражается через комплексные координаты этих
точек так:

откуда

Если положить  и , то

Условия (4) необходимы и достаточны
для того, чтобы точки А, В, С были коллинеарны. При точка С
является серединой отрезка AB, и обратно. Тогда:

c =

Пусть имеем параллелограмм ABCD. Его центр
имеет комплексную координату  =  при условии, что точки А, В, С, D имеют
соответственно комплексные координаты а, b, с, d. Если не
исключать случай вырождения параллелограмма, когда все его вершины оказываются
на одной прямой, то равенство a c = b d (5)
является необходимым и достаточным условием того, чтобы четырехугольник ABCD
был параллелограммом.

                 
C

   
B                                                              B                         
C

 N       
M                                                     MЬ            

A                               
D                             A                                          D

Рис.
5                                             Рис. 6

Задача 1. Точки М и N – середины диагоналей АС и
BD четырехугольника
ABCD. (Рис.5)

Доказать, что |AB|2 |BC|2 |CD|2 |DA|2 = |AC|2 |BD|2 4|MN|2.

Решение. Пусть точкам A,
В, С, D, М, N соответствуют комплексные числа а, b,
с, d, т, п.

Так как m =  и n = , то

|AB|2 |BC|2 |CD|2 |DA|2

|AC|2 |BD|2 4|MN|2

Равенство доказано.

Задача 2. Доказать, что если в плоскости
параллелограмма ABCD существует такая точка М, что |MA|2 |MC|2=|MB|2 |MD|2, тo ABCD
– прямоугольник. (Рис.6)

Решение. Если за начальную точку
принять центр параллелограмма ABCD, то при принятых ранее обозначениях с= -a, d= -b, и поэтому
данное в условии равенство будет эквивалентно равенству , которое
означает, что диагонали параллелограмма равны, т. е. он прямоугольник.

Уравнение высших степеней, уравнение
деления круга на пять частей

В основе решения уравнений выше второй степени
лежит теорема о рациональных корнях многочлена

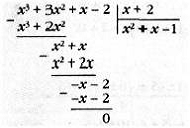
Если несократимая дробь p/q является
корнем многочлена P(x)= с целыми
коэффициентами, то её числитель p является делителем свободного
члена, а знаменатель q – делителем старшего коэффициента .

Для доказательства достаточно
подставить в ур-е P(x)=0 x=p/q и умножить
ур-е на . Получим

Все слагаемые в левой части, кроме
последнего, делятся на р, поэтому и делится на р, а поскольку q и р –
взаимно простые числа, р явл-ся делителем . Доказательство для q аналогично.

С помощью этой теоремы можно найти
все рациональные корни ур-я с целыми коэфф-ми испытанием конечного числа
«кандидатов». Например, для ур-я , старший коэфф-т которого равен 1,
«кандидатами» будут делители числа -2. Их всего четыре: 1, -1, 2, -2. Проверка
покажет, что корнем явл-ся только одно из этих чисел: .

Если один корень найден, можно
понизить степень ур-я. Согласно теореме Безу, остаток от деления многочлена P(x) на двучлен
х-с равен P(c), т.е.
Р(х)=(х-с)Q(х) Р(с).

Из теоремы непосредственно следует,
что

Если с – корень многослена Р(х), то
многочлен делится на х-с, т.е. Р(х)=(х-с)Q(х), где Q(x) –
многочлен степени, на 1 меньшей, чем Р(х).

Продолжая наш пример, вынесем из
многочлена  множитель . Чтобы
найти частное Q(x), можно
выполнить деление «уголком», как показано на рис. 7. Но есть и более простой
способ. Он станет понятен из примера:

Теперь остаётся решить квадратное
уравнение х2 х-1=0. Его корни:

Если у многочлена с целыми
коэффициентами рациональных корней не оказалось, можно попробовать разложить
его на множители меньшей степени с целыми коэффициентами. Рассмотрим, например,
уравнение:

Представим левую часть в виде
произведения двух квадратных трёхчленов с неизвестными (неопределёнными)
коэффициентами:

Раскроем скобки в правой части и
приведём подобные:

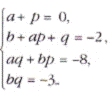
Теперь, приравнивая коэффициенты при
одинаковых степенях х в обеих частях, получим систему уравнений

Попытка решить эту систему в общем
виде вернула бы нас назад, к решению исходного уравнения. Но целые корпи, если
они существуют, нетрудно найти и подбором. Не ограничивая общности, можно
считать, что , тогда
последнее уравнение показывает, что надо рассмотреть лишь два варианта: b = 3, q=-1 и b=1, q=-3.
Подставляя эти пары значений в остальные уравнения, убеждаемся, что первая из
них даёт искомое разложение:

Этот способ решения уравнений
называется методом неопределённых коэффициентов.

Если уравнение имеет вид P(Q(x)) = 0, где
Р и Q –
многочлены, то замена у = Q(x) сводит его
решение к решению двух уравнений меньших степеней: Р(у) = 0 и Q(x) = у.
Замена используется, в частности, при решении биквадратных уравнений.

Более интересный случай – возвратные
уравнения, т. е. уравнения чётной степени

,

в которых коэффициенты, одинаково
отстоящие от концов, равны: = , =  и т. д. Такое уравнение сводится к
уравнению вдвое меньшей степени делением на и последующей заменой у = х± 1/x.

Рассмотрим, например, уравнение

.

Поделив его на х2 (что законно, так
как х = 0 не является корнем), получаем

.

Заметим, что.

Поэтому величина у = х 1/х
удовлетворяет квадратному уравнению у ау b
– 2 = 0, решив которое можно найти х из уравнения х2-ух 1 =0.

При решении возвратных уравнений
более высоких степеней обычно используют тот факт, что выражение при любом k можно
представить как многочлен степени k от у = х
1/х.

Описанные здесь приёмы используются
при исследовании (в комплексных числах) уравнения деления круга на пять частей:

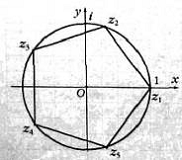
Рис. 7

Уравнение называется так потому, что
если его корпи отметить па комплексной плоскости, то они попадут в вершины
правильного пятиугольника, вписанного в единичную окружность, причём одной из
вершин будет точка с координатами (1;0) (рис.8). Используя тригонометрическое
представление комплексного числа, эти корни можно записать следующим образом:

, k=1, 2, 3, 4,
5.

Среди них находится и единственный
действительный корень ь.
Спрашивается, можно ли выразить остальные.

Попробуем сделать это.
Поскольку один корень, х=1, нам известен, понизим степень уравнения, вынося из
его левой части двучлен х-1:

Остаётся
уравнение

Оно возвратное, делим его на :

.

Подставляем z=x 1/x:

Корни этого квадратно уравнения

.

Для х получаем уравнение , или

Отсюда

.

Таким образом, наше уравнение
допускает решение в радикалах, и даже в квадратных радикалах. Последнее
означает что правильный пятиугольник можно построить с помощью циркуля и
линейки. Более того, полученные формулы указывают и конкретный способ: прежде
всего надо построить отрезки, равные действительным и мнимым частям комплексных
чисел , а затем
точки с соответствующими координатами – они и будут вершинами пятиугольника.

Заключение

Исследовав эту тему и проанализировав весь
материал, который смогли найти, мы сделали вывод, что комплексные уравнения не
только незаменимы, но и должны рассматриваться в широком спектре их
практического применения.

Метод комплексных чисел позволяет решать
планиметрические задачи по готовым формулам прямым вычислением, элементарными
выкладками. Выбор этих формул с очевидностью диктуется условиями задачи и ее
требованием. В этом состоит необычайная простота этого метода по сравнению с
координатным, векторным и другими методами, требующими от решающего порой
немалой сообразительности, длительных поисков, хотя готовое решение может быть
очень коротким.

Список использованной литературы

1.
«Энциклопедия для детей – математика» 1998 г.

.
«Энциклопедический словарь юного математика» 1997 г.