- Введение
- Курсовая работа
- Метод ньютона-котеса
- Метод средних прямоугольников
- Метод чебышева
- Метод трапеций
- Метод чебышева
- Реферат найти приближенное вычисление определенного интеграла
- Реферат: приближенное вычисление определенного интеграла при помощи квадратурной формулы чебышева –
- Список используемой литературы
- Таблица 1. значения коэффициентов ньютона-котеса
- H
- N
- H0
- Таблица 2. значения узлов квадратурной формулы чебышева
- Текст программы
- Федеральное агентство по образованию рф
Введение
На практике редко удается вычислить точно определенный
интеграл. Например, в элементарных функциях не вычисляется функция Лапласа
широко используемая в теории вероятностей для вычисления
вероятностей, связанных с нормально распределенными случайными величинами.
Задача
численного интегрирования состоит в нахождении приближенного значения
интеграла:
(1)
от
непрерывной на отрезке [a, b] функции .
Численные методы интегрирования применяются в случаях,
когда не удается найти аналитическое выражение первообразной для функции либо если функция задана
таблично. Формулы численного интегрирования называются квадратурными формулами.
Пример:
Приближенное неравенство
(2)
где qj – некоторые числа, xj – некоторые
точки отрезка [a, b], называется квадратурной формулой, определяемой весами
qj и узлами xj.
Говорят, что квадратурная формула точна для многочленов
степени m, если при замене на
произвольный алгебраический многочлен степени m приближенное равенство
(2) становится точным.
Рассмотрим некоторые широко используемые примеры
приближенного вычисления определенных интегралов, квадратурные формулы.
Курсовая работа
по курсу информатика
“ПРИБЛИЖЕННОЕ
ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА”
Тула, 2007
Содержание
Введение
Метод средних
прямоугольников
Метод ньютона-котеса
Заменим
подынтегральную функцию f(x) интерполяционным многочленом Лагранжа:
Тогда
(1)
Так как dx=hdq, то
Так как , то
Окончательно
получаем формулу Ньютона-Котеса:
(2)
Величины Hi называют коэффициентами
Ньютона-Котеса. Они не зависят от f(x). Их можно вычислить заранее для различного числа узлов n (таблица 1).
Формула
Ньютона-Котеса с n узлами точна для полиномов степени не выше n. Для получения большей
точности не рекомендуется использовать формулы с большим числом узлов, а лучше
разбивать отрезок на подотрезки, к каждому из которых применяется формула с
одним и тем же небольшим числом узлов.
Метод средних прямоугольников
Вычисление
определенного интеграла геометрически означает вычисление площади фигуры,
ограниченной кривой , прямыми х=а и х=b и осью абсцисс.
Приближенно эта площадь равна сумме площадей прямоугольников.
Обозначим , где
n – количество шагов.
Формула левых
прямоугольников:
Формула
правых прямоугольников:
Более точной
является формула средних прямоугольников:
Метод трапеций
Площадь под
кривой заменяется суммой площадей трапеций:
или
Нетрудно
убедиться, что
Поскольку
точность вычислений по приведенным формулам зависит от числа разбиений n исходного отрезка [a; b], то вычислительный
процесс целесообразно строить итерационным методом, увеличивая n до тех пор, пока не
будет выполнено условие
где – значения интеграла на шаге, а – точность вычислений.
Метод чебышева
П.Л. Чебышев
предложил формулу:
в которой
коэффициенты ci фиксированы, а хi подлежат определению.
Пользуясь
алгебраическими свойствами симметричных многочленов, опустив преобразования,
ограничимся готовыми результатами. В таблице 2 приведены значения узлов
квадратурной формулы Чебышева для некоторых значений n.
Метод
трапеций
Метод Ньютона-Котеса
Метод
чебышева
Блок-схема основной
программы
Блок-схема процедуры:
метод трапеций
Блок-схема процедуры:
метод Ньютона-Котеса
Блок-схема процедуры:
метод Чебышева
Текст программы
Список используемой
литературы
Реферат найти приближенное вычисление определенного интеграла
Приближенное решение определенного интеграла от непрерывной функции, расчет погрешностей. Способы решения дифференциальных уравнений. Абсолютная и условная сходимость числовых и степенных рядов. Интервал, свойства и радиус сходимости степенного ряда.
контрольная работа, добавлен 06.06.2021
Понятие определенного интеграла. Описание классов интегрируемых функций. Анализ свойств определенного интеграла и методов его вычисления. Примеры вычисления интеграла при помощи формулы Ньютона–Лейбница, замены переменной, интегрирования по частям.
конспект урока, добавлен 18.04.2021
Определение площади плоской фигуры, объема тел вращения, образованных при вращении вокруг оси, с помощью определенного интеграла. Понятие несобственного интеграла с бесконечными пределами интегрирования, несобственные интегралы от разрывных функций.
лекция, добавлен 09.04.2021
Задачи, приводящие к понятию определенного интеграла, сфера его применения и геометрический смысл. Вычисление площади плоской фигуры. Объёмы тел вращения. Характеристика кривых, встречаются при вычислении определенного интеграла. Исчисление длины дуги.
дипломная работа, добавлен 14.05.2021
Изучение сущности определенного интеграла – средства исследования в математике, физике, механике. Определение площади криволинейной трапеции. Ознакомление с функциями определенного интеграла. Рассмотрение геометрического смысла определенного интеграла.
контрольная работа, добавлен 17.01.2021
Вычисление площадей и объёмов с помощью двойных интегралов. Анализ сущности двойного интеграла в геометрии. Расчет интегральной суммы в криволинейном цилиндре. Площадь области, ограниченной замкнутой кривой. Нахождение определенного интеграла функции.
презентация, добавлен 17.09.2021
Понятие определенного интеграла. Алгоритмы нахождения определенного интеграла методами трапеций и средних прямоугольников. Геометрический смысл определенного интеграла. Оценка абсолютной погрешности метода трапеций. Метод левых и правых прямоугольников.
курсовая работа, добавлен 27.02.2020
Вычисление площади плоских фигур при помощи интегралов. Нахождение объема тела, длины дуги, площади поверхности вращения. Определение статических моментов, центра тяжести плоских фигур, координат центра тяжести кривых с помощью определенного интеграла.
методичка, добавлен 14.12.2021
Вычисление площади плоской фигуры с применением определенного интеграла. Определение объема тела вращения при помощи геометрических расчетов. Понятие и признаки несобственного интеграла. Несобственные интегралы с бесконечными пределами интегрирования.
лекция, добавлен 03.04.2021
Использование простейших квадратурных формул для приближенного вычисления интегралов: формулы трапеций, средних прямоугольников, Симпсона, Чебышева. Алгоритм и программная реализация метода Чебышева для нахождения значения интеграла в среде Tubro Pascal.
курсовая работа, добавлен 02.11.2021
Реферат: приближенное вычисление определенного интеграла при помощи квадратурной формулы чебышева –
КУРСОВАЯ РАБОТА студента 2-го курса: Полякова Е.В.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
ГОСУДАРСТВЕННЫЙ ХИМИКОТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Днепропетровск 2000г.
1.1. Введение.
Требуется найти определенный интеграл
I = 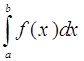
по квадратурной формуле Чебышева.
Рассмотрим, что представляет из себя вообще квадратурная формула, и как можно с ее помощью вычислить приближенно интеграл.
Известно,![]() что определенный интеграл функции
что определенный интеграл функции ![]() типа
типа 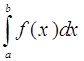 численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y=
численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y=![]() (Рис.1).
(Рис.1).
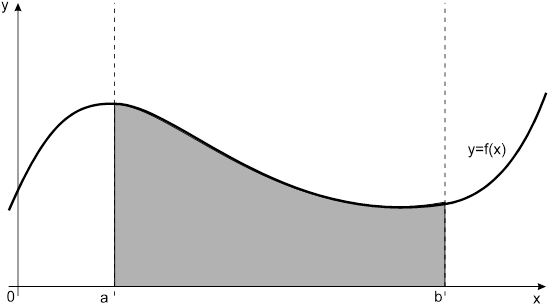
Рис. 1. Криволинейная трапеция.
Если f(x) непрерывна на отрезке [a, b], и известна ее первообразная F(x), то определенный интеграл от этой функции в пределах от а до b может быть вычислен по, известной всем, формуле Ньютона – Лейбница
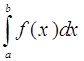 = F(b) – F(a)
= F(b) – F(a)
где
F’(x) = f(x)
Однако во многих случаях F(x) не может быть найдена, или первообразная получается очень сложной для вычисления.
Кроме того, функция часто задается таблично. Поэтому большое значение приобретает приближенное и в первую очередь численное интегрирование.
Задача численного интегрирования состоит в нахождении приближенного значения интеграла 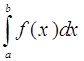 по заданным или вычисленным значениям подинтегральной функции f(x) в некоторых точках ( узлах ) отрезка [ a, b].
по заданным или вычисленным значениям подинтегральной функции f(x) в некоторых точках ( узлах ) отрезка [ a, b].
Численное определение однократного интеграла называется механической квадратурой, а соответствующие формулы численного интегрирования – квадратурными .
Заменяя подинтегральную функцию каким-либо интерполционным многочленом, мы получим квадратурные формулы вида
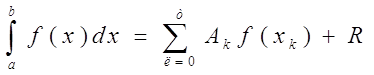
где
xk – выбранные узлы интерполяции;
Ak – коэффициенты, зависящие только от выбора узлов, но
не от вида функции (k=0,1,2,…….., n).
R – остаточный член, или погрешность квадратурной формулы.
Отбрасывая остаточный член R, мы совершаем погрешность усечения.
При расчете к ней добавляются еще различные погрешности округления.
Разобьем отрезок интегрирования [a, b] на n равных частей системой точек
xi= xo i..h; ( i = 0,1,2,……,n)
xo= a; xn= b;
h= (b-a)/n ;
и вычислим подинтегральную функцию в полученных узлах
yi= f(xi) ; ( i = 0,1,2,……,n)
1.2. Вывод формул численного интегрирования с использованием интерполяционного полинома Лагранжа
Пусть для y=f(x) известны в n 1 точках X0,X1,X2..Xn промежутка [a,b] соответствующие значения f(xi)=yi (i=0,1,2..n). Требуется приближенно найти
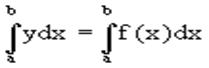
По заданным значениям Yi построим полином Лагранжа. Заменим f(x) полиномом Ln(x). Тогда
![]()
где Rn(f) – ошибка квадратурной формулы. Отсюда, воспользовавшись выражением для Ln(x), получаем приближенную квадратурную формулу:
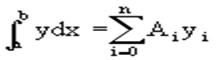
Для вычисления коэффициентов Аi заметим что:
1.коэффициенты Ai при данном расположении узлов не зависит от выбора функции f(x);
2.для полинома степени n последняя формула точная.
Пологая y=xK (k=0,1,2..,n), получим линейную систему из n 1 уравнений:
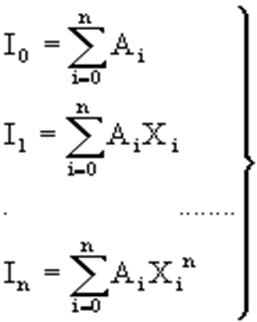
где
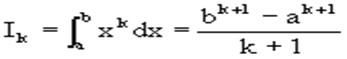
(k=0,1,..,n), из которой можно определить коэффициенты А0,А1,..,АN.
Определитель системы есть определитель Вандермонда
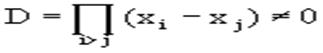
Заметим, что при применении этого метода фактическое построение полинома Лагранжа Ln(x) является излишним. Простой метод подсчета погрешности квадратурных формул разработан С.М. Никольским.
Теперь рассмотрим несколько простейших квадратурных формул :
1.3 Формула трапеций и средних прямоугольников.
Заменим дугу АВ стягивающей ее хордой, получим прямолинейную трапецию аАВb, площадь которой примем за приближенное значение интеграла
![]() y
y
0 a b x
рис 1.3.1 Криволинейная трапеция
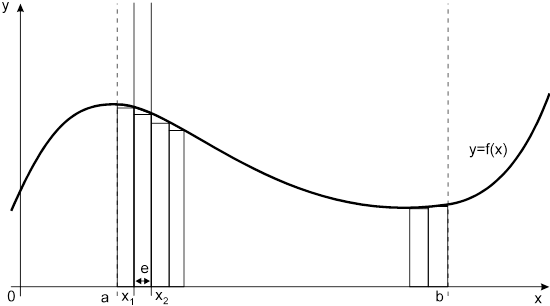
Рис. 1.3.2. Метод трапеций.
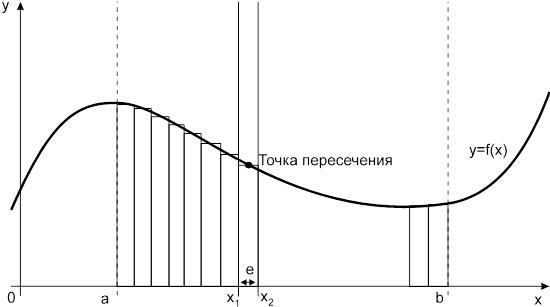
Рис. 1.3.3. Метод средних прямоугольников.
По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей —
для метода трапеций:
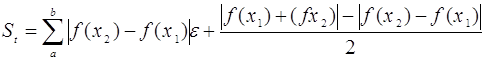 ,
,
для метода средних прямоугольников:
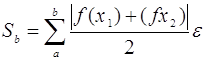 .
.
Пусть n=2m есть четное число и yi=f(xi) (i=0,1,2…n) – значения функции y=f(x) для равноотстоящих точек а=x0,x1, … ,xn=b с шагом
![]()
Применив формулу Симпсона к каждому удвоенному промежутку [x0,x2], [x2,x4] … [x2m-2,x2m] длины 2h и введя обозначения
s1=y1 y2 … y2m-1
s2=y2 y4 … y2m
получим обобщенную формулу Симпсона:
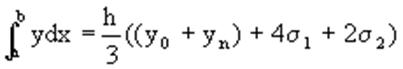
Остаточный член формулы Симпсона в общем виде:
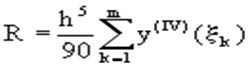
где xk I (x2к-2,x2к)
1.5. Квадратурная формула Чебышева
Рассмотрим квадратурную формулу вида:
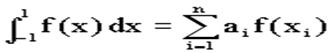
функцию f(x) будем исать в виде когда f(x) многочлен вида f(x)=ao a1x … anxn . Проинтегрировав, преобразовав и подставив значения многочлена в узлах
f(x1)=a0 a1x1 a2x12 a3x13 … anx1n
f(x2)=a0 a1x2 a2x22 a3x23 … anx2n
f(x3)=a0 a1x3 a2x32 a3x33 … anx3n
. . . . . . . . . . . . . . . .
f(xn)=a0 a1xn a2xn2 a3xn3 … anxnn
получим формулу Чебышева.
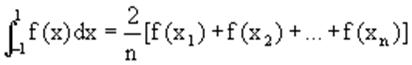
Значения х1,х2,..,хn для различных n приведены в таблице 3.
Таблица 3 – Значения х1,х2,..,хn для различных n.
| n | I | ti | n | i | ti |
| 2 | 1;2 | ± 0,577350 | 6 | 1;6 | ± 0,866247 |
| 3 | 1;3 | ± 0,707107 | 2;5 | ± 0,422519 | |
| 2 | 0 | 3;4 | ± 0,266635 | ||
| 4 | 1;4 | ± 0,794654 | 7 | 1;7 | ± 0,883862 |
| 2;3 | ± 0,187592 | 2;6 | ± 0,529657 | ||
| 5 | 1;5 | ± 0,832498 | 3;5 | ± 0,321912 | |
| 2;4 | ± 0,374541 | 4 | 0 | ||
| 3 | 0 |
2. Решение контрольного примера
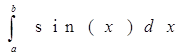
где a=0 ; b= ![]() ; при n=5;
; при n=5;
f(x) = sin(x);
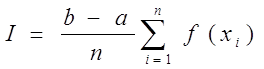
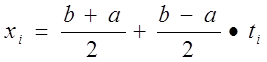
| i | xi | yi |
| 1 | 0,131489 | 0,131118 |
| 2 | 0,490985 | 0,471494 |
| 3 | 0,785 | 0,706825 |
| 4 | 0,509015 | 0,487317 |
| 5 | 0,868511 | 0,763367 |
x1= p/4 p/4*t1=p/4 p/4(-0,832498)=0,131489
x2= p/4 p/4*t2=p/4 p/4(-0,374341)=0,490985
x3= p/4 p/4*t3=p/4 p/4*0=0,785
x4=1- x2=1-0,490985 = 0,509015
x5=1- x1=1-0,131489=0,868511
y1=sin(x1) = sin(0,131489)=0,131118
y2=sin(x2) = sin(0,490985)=0,471494
y3=sin(x3) = sin(0,785)=0,706825
y4=sin(x4) = sin(0,509015)=0,487317
y5=sin(x5) = sin(0,868511)=0,763367
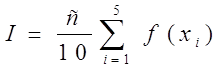
I = p/10(0,131118 0,471494 0,706825 0,487317 0,763367) =
=p/10*2,560121=0,8038779.
3. Описание программы Integral. pas. Алгоритм.
Процедура VVOD – заполняет массив, содержащий в себе аргументы xi
Процедура FORM – используя массив, содержащий аргументы xi заполняет массив yi
Процедура CHEB – используя массивы xi и yi, высчитывает по квадратурной формуле Чебышева приближенное значение интеграла.
Процедура TABL – это подпрограмма, осуществляющая вывод таблицы узлов (аргумент – функция)
При запуске программы нужно ввести границы интегрирования.
После ввода границ интегрирования используется процедура VVOD, а затем высчитывается и выводиться на экран шаг табулирования функции h.
После этого используем процедуры FORM и CHEB .
Получив результат, выводим таблицу ( процедура TABL ) и интеграл.
4. Заключение и выводы.
Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное.
Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же очень важно то, какой будет взят шаг интегрирования.
Хотя численные методы и не дают очень точного значения интеграла, но они очень важны, так как не всегда можно решить задачу интегрирования аналитическим способом.
Листинг программы.
Программа написана на языке Tubro Pascal 7.0 для MS-DOS. Ниже приведен ее листинг:
program integral;
uses crt;
const n=5;
k=-0.832498;
l=-0.374541;
z=0.0;
type aa=array[1..n] of real;
var x,y:aa;
a,b,h,ich:real;
{ заполнение х-сов в массив х[5] }
procedure vvod(var a,b:real;var c:aa);
var i:integer;
t:aa;
Begin
t[1]:=k;
t[2]:=l;
t[3]:=z;
t[4]:=l;
t[5]:=k;
for i:=1 to n-1 do
c[i]:=((b a)/2 (b-a)/2*t[i]);
for i:=n-1 to n do
c[i]:=1 – c[n 1-i];
end;
{ заполнение y-ков в массиве у[5] }
procedure form(var x:aa; var y:aa);
var i:integer;
Begin
for i:=1 to n do
y[i]:=sin(x[i]); {функция}
end;
{ процедура для расчета интеграла по квадратурной
формуле Чебышева }
procedure cheb(var y:aa;var ich:real);
var i:integer;
Begin
ich:=0;
for i:=1 to n do
ich:=ich y[i]*h;
end;
{ процедура вывода таблицы}
procedure tabl;
var i:integer;
Begin
writeln(‘ ___________________________________ ‘);
writeln(‘| i | t| x|y |’);
writeln(‘ ___________________________________ ‘);
writeln(‘| 1 |’,k:9:6,’|’,x[1]:9:6,’ |’,y[1]:9:6,’|’);
writeln(‘| 2 |’,l:9:6,’|’,x[2]:9:6,’ |’,y[2]:9:6,’|’);
writeln(‘| 3 |’,z:9:6,’|’,x[3]:9:6,’ |’,y[3]:9:6,’|’);
writeln(‘| 4 |’,l:9:6,’|’,x[4]:9:6,’ |’,y[4]:9:6,’|’);
writeln(‘| 5 |’,k:9:6,’|’,x[5]:9:6,’ |’,y[5]:9:6,’|’);
writeln(‘ ___________________________________ ‘);
end;
Begin
clrscr;
writeln(‘ П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я’);
writeln(‘ О П Р Е Д Е Л Е Н Н О Г ОИ Н Т Е Г Р А Л А ‘);
writeln;
writeln(‘Введите границы интегрирования a,b:’);
readln(a,b);
vvod(a,b,x);
h:=(b-a)/n;
writeln(‘h=’,h:9:6);
form(x,y);
cheb(y,ich);
tabl;
writeln(‘I=’,ich:8:6);
end.
Вывод результата :
П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я
О П Р Е Д Е Л Е Н Н О Г ОИ Н Т Е Г Р А Л А
Введите границы интегрирования a,b:
0 1.5708
h= 0.314160
____________________________
| i | t | x | y |
____________________________
| 1 |-0.832498| 0.131556 | 0.131177|
| 2 |-0.374541| 0.491235 | 0.471716|
| 3 | 0.000000| 0.785400 | 0.707108|
| 4 |-0.374541| 0.508765 | 0.487099|
| 5 |-0.832498| 0.868444 | 0.763325|
____________________________
I=0.804383
литературы:
1. Ракитин Т.А., Первушин В.А. “Практическое руководство по численным методам с приложением программ на языке Basic“
2. Крылов В.И. “Приближенные вычисления интегралов“ – М. : Физмат.
3. Демидович и Марон “Основы вычислительной математики“
4. Копченова и Марон “Вычислительная математика в примерах и задачах”
5. Вольвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для ПЭВМ ЕС. Минск.: 1989 г.
6. Зуев Е.А. Язык программирования Turbo Pascal. М.1992 г.
7. Скляров В.А. Знакомьтесь: Паскаль. М. 1988 г.
Список используемой литературы
1. Бахвалов Н.С.
«Численные методы». М.: Наука, 1987 – 598 с.
2. Калиткин Н.Н.
«Численные методы». М.: Наука, 1988 – 512 с.
3. Крылов В.И. «Вычислительные
методы». М.: Наука, 1977 – 408 с.
4. Нечаев В.И., Нечаева О.А.,
Почуева Л.Н. «Численные методы». Тула, 1999.
Таблица 1. значения коэффициентов ньютона-котеса
H | N | |||
1 | 2 | 3 | 4 | |
H0 | 1/2 | 1/6 | 1/8 | 7/90 |
H1 | 1/2 | 3/8 | 16/45 | |
H2 | – | 1/6 | 3/8 | 2/15 |
H3 | – | – | 1/8 | 16/45 |
H4 | – | – | – | 7/90 |
Интересно
отметить, что из формулы (2) следуют как частные случаи: формула трапеций при n=1
формула
Симпсона при n=2
правило трех
восьмых при n=3
Формулу (2)
при n>6
не применяют, так как коэффициенты Ньютона-Котеса становятся слишком большими и
вычислительная погрешность резко возрастает.
Таблица 2. значения узлов квадратурной формулы чебышева
Число интервалов n | Номер узла i | Значение узла Xi |
1 | 1 2 | 0,211325 0,788675 |
2 | 1 2 3 | 0,146447 0,500000 0,853553 |
3 | 1 2 3 4 | 0,102673 0,406204 0,593796 0,897327 |
4 | 1 2 3 4 5 | 0,083751 0,312730 0,500000 0,687270 0,916249 |
5 | 1 2 3 4 5 | 0,066877 0,288740 0,366682 0,633318 0,712260 0,933123 |
Для любых
пределов интегрирования имеем:
где ,
Значения xi берутся из таблицы при
выбранном значении n. Для повышения точности можно не только увеличивать количество
узлов, но и разбивать отрезок [a, b] на подотрезки, к каждому из которых применяется соответствующая
формула. Не рекомендуется применять формулы с большим количеством узлов (n>=8).Доказано, что для
n=8 построить квадратурную
формулу Чебышева невозможно.
Блок-схема
основной программы
Блок-схема
процедуры: метод трапеций
Блок-схема
процедуры: метод Ньютона-Котеса
Блок-схема
процедуры: метод Чебышева
Текст программы
program Curs;
uses crt, graph;
var i, n:integer;
t:byte;
a, b, eps, h:real;
x, sum1, sum2, seps, m0, m1, m2, m3, m4:real;
lf:text;
st:string;
function f (x:real):real;
begin
f:=19.44*exp (0.224*x);
end;
procedure gr (xn, xk:real);
var x, y, mx, my, dx, dy,
ymin, ymax, xh:real;
xb, yb, xm, ym, xl, yv, xp, yn, bord1, bord2,
bord3, bord4, xt, yt, xt1, yt1, dxp, dyp, nd, nr, i, kx, ky, k:integer;
st:string;
begin
k:=100;
xh:=(xk-xn)/100;
ymax:=f(xn);
dx:=(xk-xn)/100;
for i:=1 to 100 do
begin x:=xn dx*i;
y:=f(x);
if y>ymax then ymax:=y;
end;
ymin:=0;
ymax:=round(ymax);
nd:=detect;
initgraph (nd, nr, ‘c:tp7bgi’);
bord1:=60; kx:=6;
bord2:=30; ky:=8;
bord3:=30;
bord4:=80;
xb:=0; yb:=0; xm:=getmaxx; ym:=getmaxy;
xl:=xb bord1;
xp:=xm-bord2;
yv:=yb bord3;
yn:=ym-bord4;
dxp:=(xp-xl) div kx;
dyp:=(yn-yv) div ky;
dx:=(xk-xn)/kx;
dy:=(ymax-ymin)/ky;
xl:=xp-dxp*kx;
yn:=yv dyp*ky;
mx:=(xp-xl)/(xk-xn);
my:=(yn-yv)/(ymax-ymin);
setfillstyle (1,15);
bar (xb, yb, xm, ym);
setcolor(0);
setlinestyle (0,0,1);
bar (xl, yv, xp, yn);
settextjustify (0,2);
settextstyle (2,1,4);
setcolor(9);
for i:=0 to kx do begin
xt:=xl dxp*i;
str (xn dx*i:6:3, st);
line (xt, yn‑3, xt, yn 3);
outtextxy (xt 4, yn 8, st);
end;
settextstyle (0,0,1);
for i:=0 to ky do begin
yt:=yv dyp*i;
str (ymax-dy*i:6:3, st);
line (xl‑3, yt, xl 3, yt);
outtextxy (xl‑56, yt‑4, st);
end;
outtextxy (xl 100, bord3 div 2,’y=19.44*exp
(0.224*x)’);
setcolor(12);
if xn*xk<0 then begin
xt:=xl-trunc (xn*mx);
line (xt, yv, xt, yn);
end;
if ymax*ymin<0 then begin
yt:=yv trunc (ymax*my);
line (xl, yt, xp, yt);
end;
xh:=(xk-xn)/5;
for i:=0 to 5 do begin
setcolor(3);
x:=xn xh*i;
y:=f(x);
xt:=xl trunc((x-xn)*mx);
yt:=yv trunc((ymax-y)*my);
circle (xt, yt, 3);
if i>0 then
line (xt, yt, xt1, yt1);
setcolor(5);
rectangle (xt1, yt1, xt, yn);
xt1:=xt;
yt1:=yt;
end;
repeat until keypressed;
closegraph;
end;
function pr:real;
var s, x:real;
begin
s:=0;
x:=a;
for i:=1 to n do
begin
s:=s abs (f(x))*h;
x:=x h;
end;
pr:=s;
end;
function tr:real;
var s, x:real;
begin
s:=0;
x:=a;
for i:=1 to n do
begin
s:=s (f(x) f (x h))/2*h;
x:=x h;
end;
tr:=s;
end;
function ch:real;
var s, dp, kf, a1, b1:real;
s:=0;
kf:=sqrt (1/3);
for i:=2 to n 1 do
begin
a1:=a h*(i‑2);
b1:=a1 h;
s:=s ((b1‑a1)/2)*(f((a1 b1)/2‑kf*((b1‑a1)/2)) f((a1 b1)/2 kf*((b1‑a1)/2)));
end;
ch:=s;
end;
function si:real;
var s, x, f1, f2:real;
begin
s:=0;
x:=a;
i:=1;
f1:=0;
repeat
f1:=f1 f (a h*i);
i:=i 2;
until i>=n;
i:=2;
f2:=0;
repeat
f2:=f2 f (a h*i);
i:=i 2;
until i>=n;
s:=h/3*(f(a) f (b-h) (4*f1) (2*f2));
si:=s;
end;
begin
assign (lf, ‘otchet.txt’);
rewrite(lf);
clrscr;
write (‘Введите значение левого предела интегрирования: ‘);
readln(a);
write (‘Введите значение правого предела интегрирования: ‘);
readln(b);
write (‘Введите значение погрешности: ‘); readln(eps);
write (‘Введите начальное значение количества разбиений: ‘);
readln(n);
writeln;
gr (a, b);
write (‘Ждите, идет обработка данных ‘);
m0:=0;
writeln (lf, ‘ КУРСОВАЯ РАБОТА’);
writeln (lf, ‘ ПО КУРСУ ИНФОРМАТИКА’);
writeln (lf, ‘ «ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ’);
writeln (lf, ‘ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА» ‘);
writeln (lf, ‘ Выполнил: студент гр. ‘);
writeln (lf, ‘ Вариант 22 y=19.44*exp (0.224*x)’);
writeln (lf, ‘ Xn=’, a:5:3,’ Xk=’, b:5:3,’
Eps=’, eps:5:3);
writeln(lf);
writeln (lf, ‘ РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ’);
repeat
h:=abs (b-a)/n;
m1:=pr;
m2:=tr;
m3:=si;
m4:=ch;
seps:=abs (m1‑m0);
writeln (lf, ‘ │’, n:7,’ │’,
m1:11:8,’│’, m2:11:8,’│’, m3:11:8,’│’, m4:11:8,’│’, seps:11:8,’│’);
m0:=m1;
n:=n 200;
until (seps<=eps);
clrscr;
reset(lf);
while not eof(lf) do
begin
readln (lf, st);
writeln(st);
end;
{write (‘Нажмите <Enter> для выхода из программы’);
close(lf);
end.
Федеральное
агентство по образованию рф
Тульский государственный
университет
Кафедра АОТ и ОС







