Реферат: интеграл и его свойства –
Теоретические вопросы
- Понятие первообразной функции. Теорема о первообразных.
Основной задачей дифференциального исчисления
является нахождение производной f’(x)
или дифференциала df=f’(x)dx
функции f(x).
В интегральном исчислении решается обратная задача. По заданной функции f(x
) требуется найти такую функцию F(x),
что F’(х)=f(x)
или dF(x)=F’(x)dx=f(x)dx.
Таким образом, основной задачей интегрального исчисления
является восстановление функции F(x)
по известной производной (дифференциалу) этой функции. Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т. д..
Определение.Функция F(x), ![]() , называется первообразной для функции f(x) на множестве Х, если она дифференцируема для любого
, называется первообразной для функции f(x) на множестве Х, если она дифференцируема для любого ![]() и F’(x)=f(x) или dF(x)=f(x)dx.
и F’(x)=f(x) или dF(x)=f(x)dx.
Теорема.Любая непрерывная на отрезке [a; b] функция f(x) имеет на этом отрезке первообразную F(x).
Теорема. Если F1
(x) и F2
(x) – две различные первообразные одной и той же функции f(x) на множестве х , то они отличаются друг от друга постоянным слагаемым, т. е. F2
(x)=F1x) C, где С – постоянная
.
- Неопределенный интеграл, его свойства.
Определение.Совокупность F(x) C всех первообразных функции f(x) на множестве Х называется неопределенным интегралом и обозначается:
![]() – (1)
– (1)
В формуле (1) f(x)dx
называется подынтегральным выражением, f(x) – подынтегральной функцией, х – переменной интегрирования,
а С – постоянной интегрирования.
Рассмотрим свойства неопределенного интеграла, вытекающие из его определения.
1. Производная из неопределенного интеграла равна подынтегральной функции, дифференциал неопределенного интеграла равен подынтегральному выражению:
![]() и
и ![]() .
.
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
![]()
3. Постоянный множитель а (а≠0) можно выносить за знак неопределенного интеграла:
![]()
![]()
4. Неопределенный интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций:
![]()
5. Если F(x) – первообразная функции f(x), то:
![]()
6 (инвариантность формул интегрирования). Любая формула интегрирования сохраняет свой вид, если переменную интегрирования заменить любой дифференцируемой функцией этой переменной:
![]()
где u – дифференцируемая функция.
- Таблица неопределенных интегралов.
Приведем основные правила интегрирования функций.
I. ![]()
II. ![]()
III. ![]()
IV. ![]()
V. ![]()
VI. ![]()
Приведем таблицу основных неопределенных интегралов.
(Отметим, что здесь, как и в дифференциальном исчислении, буква u
может обозначать как независимую переменную (u=x)
, так и функцию от независимой переменной (u=u(x))
.)
1. ![]() (n≠-1).
(n≠-1).
2. ![]() (a >0, a≠1).
(a >0, a≠1).
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
![]()
12. ![]()
13. ![]()
14. ![]() (a≠0).
(a≠0).
15.![]() (a≠0).
(a≠0).
16. ![]() (|u| > |a|).
(|u| > |a|).
17. ![]() (|u| < |a|).
(|u| < |a|).
18. ![]()
19. ![]()
Интегралы 1 – 17 называют табличными.
Некоторые из приведенных выше формул таблицы интегралов, не имеющие аналога в таблице производных, проверяются дифференцированием их правых частей.
- Замена переменной и интегрирование по частям в неопределенном интеграле.
Интегрирование подстановкой (замена переменной).
Пусть требуется вычислить интеграл ![]() , который не является табличным. Суть метода подстановки состоит в том, что в интеграле
, который не является табличным. Суть метода подстановки состоит в том, что в интеграле ![]() переменную х
переменную х
заменяют переменной t
по формуле x=φ(t),
откуда dx=φ’(t)dt.
Теорема. Пусть функция x=φ(t) определена и дифференцируема на некотором множестве Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула:
![]() – (2)
– (2)
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Интегрирование по частям.
Метод интегрирования по частям следует из формулы дифференциала произведения двух функций. Пусть u(x)
и v(x)
– две дифференцируемые функции переменной х
. Тогда:
d(uv)=udv vdu. – (3)
Интегрируя обе части равенства (3), получаем:
![]()
Но так как ![]() , то:
, то:
![]() – (4)
– (4)
Соотношение (4) называется формулой интегрирования по частям
. С помощью этой формулы отыскание интеграла ![]() . Применять ее целесообразно, когда интеграл в правой части формулы (4) более прост для вычисления, нежели исходный.
. Применять ее целесообразно, когда интеграл в правой части формулы (4) более прост для вычисления, нежели исходный.
В формуле (4) отсутствует произвольная постоянная С
, так как в правой части этой формулы стоит неопределенный интеграл, содержащий произвольную постоянную.
Приведем некоторые часто встречающиеся типы интегралов, вычисляемых методом интегрирования по частям.
I. Интегралы вида ![]() ,
, ![]() ,
, ![]() (Pn
(Pn
(x)
– многочлен степени n, k
– некоторое число). Чтобы найти эти интегралы, достаточно положить u=Pn
(x)
и применить формулу (4) n
раз.
II. Интегралы вида ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (Pn(x) – многочлен степени nотносительно х
(Pn(x) – многочлен степени nотносительно х
). Их можно найти по частым, принимая за u
функцию, являющуюся множителем при Pn
(x).
III. Интегралы вида ![]() ,
, ![]() (a, b
(a, b
– числа). Они вычисляются двукратным интегрированием по частям.
5. Разложение дробной рациональной функции на простейшие дроби.
Рациональной дробью R(x)
называется дробь, числителем и знаменателем которой являются многочлены, т. Е. всякая дробь вида:
![]()
Если степень многочлена в числителе больше или равна степени многочлена в знаменателе (n≥m)
, то дробь называется неправильной
. Если степень многочлена в числителе меньше степени многочлена в знаменателе (n≤m)
, то дробь называется правильной.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби (это представление достигается путем деления числителя на знаменатель по правилу деления многочленов):
![]()
где R(x)
– многочлен-частное (целая часть) дроби ![]() ; Pn
; Pn
(x)
– остаток (многочлен степени n < m
).
6. Интегрирование простейших дробей. Интегрирование рациональных дробей.
Интегрирование простейших дробей.
Простейшей дробью называется правильная рациональная дробь одного из следующих четырех типов:
1) ![]()
2) ![]() (n≥2);
(n≥2);
3) ![]()
4) ![]() (n≥2).
(n≥2).
Здесь А, a, p, q, M, N– действительные числа, а трехчлен не имеет действительных корней, т. е. p2
/4-q < 0.
Простейшие дроби первого и второго типов интегрируются непосредственно с помощью основных правил интегрального исчисления:
![]()
![]()
Интеграл от простейшей дроби третьего типа приводится к табличным интегралам путем выделения в числителе дифференциала знаменателя и приведения знаменателя к сумме квадратов:
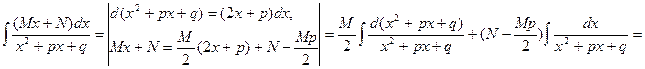
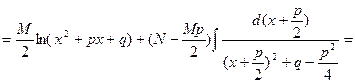
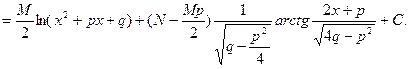
Интегрирование рациональных дробей.
Разложение рациональной дроби на простейшие дроби
.
Всякую правильную рациональную дробь ![]() можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения
можно представить в виде суммы конечного числа простейших рациональных дробей первого – четвертого типов. Для разложения ![]() на простейшие дроби необходимо разложить знаменатель Qm
на простейшие дроби необходимо разложить знаменатель Qm
(x)
на линейные и квадратные множители, для чего надо решить уравнение:
![]() – (5)
– (5)
Теорема. Правильную рациональную дробь![]() , где
, где![]() , можно единственным образом разложить на сумму простейших дробей:
, можно единственным образом разложить на сумму простейших дробей:
![]()
![]() – (6)
– (6)
(A1
, A2
, …, Ak
, B1
, B2
, …, B1
, M1
, N1
, M2
, M2
, …, Ms
, Ns
– некоторые действительные числа).
Метод неопределенных коэффициентов.
Суть метода неопределенных коэффициентов состоит в следующем. Пусть дано разложение правильной рациональной дроби ![]() по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Qm
по формуле (6) на простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к общему знаменателю Qm
(x)
и приравняем многочлен, получившийся в числителе, многочлену Pn
(x).
Метод частных значений.
При нахождении неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при одинаковых степенях х
, можно дать переменной х
несколько частных значений (по числу неопределенных коэффициентов) и получить таким образом систему уравнений относительно неопределенных коэффициентов. Особенно выгодно применять этот метод в случае, корни знаменателя рациональной дроби ![]() просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.
просты и действительны. Тогда оказывается удобным последовательно полагать равным каждому из корней знаменателя.
Правило интегрирования рациональных дробей.Для того чтобы проинтегрировать рациональную дробь, необходимо выполнить следующие действия:
1) если рассматриваемая рациональная дробь ![]() – неправильная (k≥m), представить ее в виде суммы многочлена и правильной рациональной дроби:
– неправильная (k≥m), представить ее в виде суммы многочлена и правильной рациональной дроби:
![]()
где n < m; R(x) – многочлен;
2) если рассматриваемая рациональная дробь ![]() – правильная (n < m), представить ее в виде суммы простейших рациональных дробей по формуле (6);
– правильная (n < m), представить ее в виде суммы простейших рациональных дробей по формуле (6);
3) интеграл от рациональной дроби представить в виде суммы интегралов от целой части и от соответствующих простейших дробей и вычислить эти интегралы.
- Интегрирование выражений, содержащие тригонометрические функции.
Интегралы вида ![]() Универсальная подстановка.
Универсальная подстановка.
Будем рассматривать интегралы вида:
![]()
– (7)
при условии, что они не являются табличными. Вычислить их можно различными методами, изложенными ранее. Иногда бывает достаточно преобразовать подынтегральное выражение, использовав тригонометрические формулы, применить методы «подведения» множителя под знак дифференциала, замены переменной или интегрирования по частям.
Для вычисления интеграла вида (7) существует общая универсальная схема вычисления, основанная на универсальной тригонометрической подстановке ![]() .
.
Интегралы вида![]()
![]() (m, n є Z, m ≥ 0, n ≥ 0).
(m, n є Z, m ≥ 0, n ≥ 0).
Если хотя бы одно из чисел m
и n
– нечетное, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы sin2x cos2x=1
оставшуюся четную степень через конфункцию, приходим к табличному интегралу.
Интегралы вида![]() ,
, ![]() , (n є N, n > 1).
, (n є N, n > 1).
Эти интегралы вычисляются подстановками tgx= t
и ctgx=t
соответсвенно.
Если t=tgx
, то x=arctgt
, ![]() . Тогда:
. Тогда:
![]() .
.
Последний интеграл при n ≥ 2
является интегралом от неправильной рациональной дроби, которая вычисляется по правилу интегрирования рациональных дробей.
Аналогично если t=ctgx
, то x=arcctgt
, ![]() , откуда:
, откуда:
![]()
Интегралы вида![]()
![]()
![]() (m, n є R).
(m, n є R).
Они вычисляются путем разложения подынтегральной функции на слагаемые по формулам:
![]()
![]()
![]()
8.Интегрирование иррациональных выражений.
Интегралы вида![]()
(m1
, n1
, m2
, n2
, … – целые числа). В этих интегралах подынтегральная функция рациональна относительно переменной интегрирования и радикалов от х
. Они вычисляются подстановкой x=ts
, где s
– общий знаменатель дробей ![]() ,
, ![]() , … При такой замене переменной все отношения
, … При такой замене переменной все отношения ![]() = r1
= r1
, ![]() = r2
= r2
, … являются целыми числами, т. е. интеграл приводится к рациональной функции от переменной t
:
![]()
![]()
Интегралы вида
(m1
, n1
, m2
, n2
, … – целые числа). Эти интегралы подстановкой:
![]()
где s
– общий знаменатель дробей ![]() ,
, ![]() , …, сводятся к рациональной функции от переменной t
, …, сводятся к рациональной функции от переменной t
.
Интегралы вида ![]()
![]()
![]()
Для вычисления интеграла I1
выделяется полный квадрат под знаком радикала:

и применяется подстановка:
![]() , dx=du.
, dx=du.
В результате этот интеграл сводится к табличному: ![]()
В числителе интеграла I2
выделяется дифференциал выражения, стоящего под знаком радикала, и этот интеграл представляется в виде суммы двух интегралов:
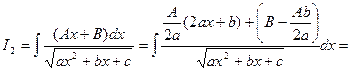
![]()
![]()
![]()
![]()
где I1
– вычисленный выше интеграл.
Вычисление интеграла I3
сводится к вычислению интеграла I1
подстановкой:
![]()
![]()
Интеграл вида ![]()
Частные случаи вычисления интегралов данного вида рассмотрены в предыдущем пункте. Существует несколько различных приемов их вычисления. Рассмотрим один из таких приемов, основанный на применении тригонометрических подстановок.
Квадратный трехчлен ax2
bx c
путем выделения полного квадрата и замены переменной может быть представлен в виде ![]() Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
Таким образом, достаточно ограничиться рассмотрением трех видов интегралов:
![]()
![]()
![]()
Интеграл ![]() подстановкой
подстановкой
u=k
sint
(или u=k
cost
)
сводится к интегралу от рациональной функции относительно sintи cost.
Интегралы вида![]()
(m, n, p єQ
, a, b є R
). Рассматриваемые интегралы, называемые интегралами от дифференциального бинома ![]() , выражаются через элементарные функции только в следующих трех случаях:
, выражаются через элементарные функции только в следующих трех случаях:
1) если p є Z
, то применяется подстановка:
x=ts
,
где s
– общий знаменатель дробей mи n
;
2) если ![]() Z
Z
, то используется подстановка:
a bxn
=ts
,
где s
– знаменатель дроби ![]()
3) если ![]() Z
Z
, то применяется подстановка:
ax-n
b=ts
,
где s
– знаменатель дроби ![]()
9. Понятие определенного интеграла, его геометрический смысл.
Определение.Если существует конечный передел интегральной суммы (8)
![]() – (8)
– (8)
при λ→0, не зависящий от способа разбиения τn
отрезка [a; b] на частичные отрезки и выбора промежуточных точек ξk
, то этот предел называют определенным интегралом (или интегралом Римана) от функции f(x) на отрезке [a; b] и обозначают:
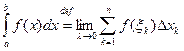
Если указанный предел существует, то функция f(x)
называется интегрируемой на отрезке
[a; b] (или интегрируемой по Риману
). При этом f(x)dx
называется подынтегральным выражением, f(x)
– подынтегральной функцией, х – переменной интегрирования, a
и b
– соответственно нижним
и верхним пределами интегрирования.
Определенный интеграл есть число, равное пределу, к которому стремится интегральная сумма, в случае, когда диаметр разбиения λ стремится к нулю.
Геометрический смысл определенного интеграла.
Пусть функция y=f(x)
непрерывна на отрезке [a; b] и f(x) ≥ 0
. Фигура, ограниченная графиком АВ
функции y=f(x),
прямыми x=a, x=b
и осью Ох
(рис. 1), называется криволинейной трапецией
.
 Интегральная сумма и ее слагаемые имеют простой геометрический смысл: произведение
Интегральная сумма и ее слагаемые имеют простой геометрический смысл: произведение ![]() равно площади прямоугольника с основанием
равно площади прямоугольника с основанием ![]() и высотой
и высотой ![]() , а сумма
, а сумма ![]() представляет собой площадь заштрихованной ступенчатой фигуры (изображенной на рис. 1). Очевидно, что эта площадь зависит от разбиения τn
представляет собой площадь заштрихованной ступенчатой фигуры (изображенной на рис. 1). Очевидно, что эта площадь зависит от разбиения τn
отрезка [a; b] на частичные отрезки и выбора точек ξk
.
Чем меньше ![]() , k=1, n,
, k=1, n,
тем площадь ступенчатой фигуры ближе к площади криволинейной трапеции. Следовательно, за точную площадь S
криволинейной трапеции принимается предел интегральной суммы при λ→0
:
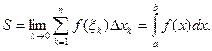
Таким образом, с геометрической точки зрения определенный интеграл от неотрицательной функции численно равен площади соответствующей криволинейной трапеции.
10. Основные свойства определенного интеграла.
Рассмотрим свойства определенного интеграла.
1. Если нижний и верхний пределы интегрирования равны (a=b), то интеграл равен нулю:
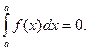
Это свойство следует из определения интеграла.
2. Если f(x)=1, то

Действительно, так как f(x)=1
, то
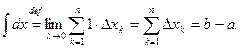
3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
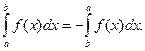
4. Постоянный множитель можно выносить за знак определенного интеграла:
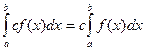
![]() R
R
.
5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f1
(x), f2
(x), …, fn
(x) равен алгебраической сумме определенных интегралов от слагаемых:
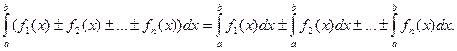
6 (аддитивность определенного интеграла). Если существует интегралы  и
и  то существует также интеграл
то существует также интеграл  и для любых чисел a, b, c;
и для любых чисел a, b, c;
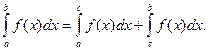
7. Если f(x) ≥ 0 ![]() [a; b], то
[a; b], то
 a < b.
a < b.
8 (определенность определенного интеграла). Если интегрируемые функции f(x) и φ(x) удовлетворяют неравенству f(x) ≥ φ(x) ![]() [a; b], то
[a; b], то
 a >b.
a >b.
9 (об оценке определенного интеграла). Если m и М – соответственно нименьшее и наибольшее значения функции f(x), непрерывной на отрезке [a; b], то
 a < b.
a < b.
10 (теорема о среднем). Если функция f(x) непрерывна на отрезке [a; b], то существует такая точка ![]() [a; b], что
[a; b], что
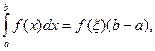
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [a; b] и длины b-a этого отрезка.
11. Теорема о среднем.
Если функция f(x) непрерывна на отрезке [a; b], то существует такая точка ![]() [a; b], что
[a; b], что
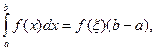
т. е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [a; b] и длины b-a этого отрезка.
12. Производная определенного интеграла по верхнему пределу. Формула Ньютона-Лейбница.
До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a
и b
. Если оставить постоянным нижний предел интегрирования a
, а верхний х
изменять так, чтобы x є [a; b],
то величина интеграла будет изменяться. Интеграл вида:
 xє [a; b],
xє [a; b],
называется определенным интегралом с переменным верхним пределом
и является функцией верхнего предела х
. Здесь для удобства переменная интегрирования обозначена буквой t
, а верхний предел интегрирования – буквой х
.
Теорема.Производная определенного интеграла от непрерывной функции f(x) по его переменному верхнему пределу существует и равна подынтегральной функции, в которой вместо переменной интегрирования подставлено значение верхнего предела:
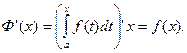
Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница дает правило вычисления определенного интеграла: значение определенного интеграла на отрезке [a; b] от непрерывной функции f(x) равно разности значений любой ее первообразной, вычисленной при x=b и x=a.
 – (9)
– (9)
13. Замена переменной и интегрирования по частям в определенном интеграле.
Замена переменнойв определенном интеграле.
Этот метод, как и в случае неопределенного интеграла, позволяет упростить вычисления, т. е. привести подынтегральное выражение к соответствующей табличной форме. Применение замены переменной в определенном интеграле базируется на следующей теореме.
Теорема. Если функция f(x) непрерывная на отрезке [a; b], а функция x=φ(t) непрерывно дифференцируема на отрезке [t1
; t2
], причем φ([t1
; t2
])=[a; b] и φ(t1
)=a, φ(t2
)=b, то справедлива формула:
 – (10)
– (10)
Интегрирование по частям в определенном интеграле.
Пусть u(x)
и v(x)
– дифференцируемые на отрезке [a; b]
функции переменной х
. Тогда d(uv)=udv vdu.
Проинтегрируем обе части последнего равенства на отрезке [a; b]
:
 – (11)
– (11)
С другой стороны, по формуле Ньютона-Лейбница
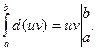
Следовательно, формула (11) принимает вид:
 – (12)
– (12)
Формула (12) называется формулой интегрирования по частям в определенном интеграле.
15. Вычисление площадей плоских фигур.
Площадь криволинейной трапеции, ограниченной кривой y=f(x) [f(x) ≥ 0],
прямыми x=a
и x=b
и отрезками [a; b]
оси Ох
, вычисляется по формуле:

Площадь фигуры, ограниченной кривыми y=f1
(x)
и y=f2
(x)[f1
(x) ≤ f2
(x)]
и прямыми x=a
и x=b
, находится по формуле:
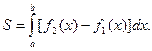
Если кривая задана параметрическими уравнениями x=x(t), y=y(t),
то площадь криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b
и отрезком [a; b]
оси Ох
, выражается формулой:
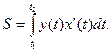
где t1
и t2
определяются из уравнений a=x(t1
), b=x(t2
) [y(t) ≥ 0
при t1
≤ t ≤ t2
].
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением ρ=ρ(θ)
и двумя полярными радиусами θ=α, θ=β (α < β),
выражается интегралом:
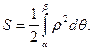
16. Определение и вычисление длины кривой, дифференциал кривой.
Если кривая y=f(x)
на отрезке [a; b]
– гладкая (т. е. производная y’=f’(x)
непрерывна), то длина соответствующей дуги этой кривой находится по формуле:
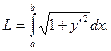
При параметрическом задании кривой x=x(t), y=y(t) [x(t)
и y(t)
– непрерывно дифференцируемые функции] длина дуги кривой, соответствующая монотонному изменению параметра t
от t1
до t2
, вычисляется по формуле:
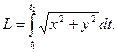
Если гладкая кривая задана в полярных системах координатах уравнением ρ=ρ(θ)
, α ≤ θ ≤ β
, то длина дуги равна:
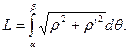
Дифференциал длины дуги.
Длина дуги кривой определяется формулой:
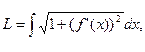
где y=f(x) ![]() [a; b].
[a; b].
Предположим, что в этой формуле нижний передел интегрирования остается постоянным, а верхний изменяется. Обозначим верхний предел буквой х
, а переменную интегрирования буквой t
. Длина дуги будет функцией верхнего предела:
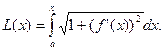
Практические задания
1. Найти неопределенный интеграл, результат проверить дифференцированием:
1) ![]() .
.
Решение:
![]()
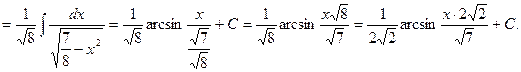
Проверка:
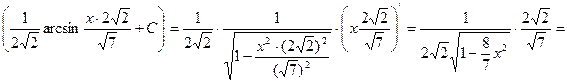
 – верно.
– верно.
___________________________________________________________________________
2) ![]() .
.
Решение:
![]()
![]()
Проверка:
![]() – верно.
– верно.
__________________________________________________________________________________
3) ![]() .
.
Решение:
![]()
![]()
![]()
![]()
Проверка:
![]() – верно.
– верно.
___________________________________________________________________________
4) ![]() .
.
Решение:
![]()
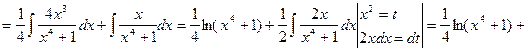
![]()
Проверка:
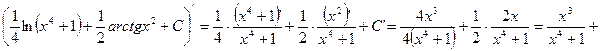
![]() – верно.
– верно.
___________________________________________________________________________
5) ![]() .
.
Решение:
![]()
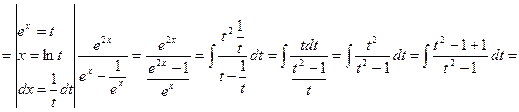
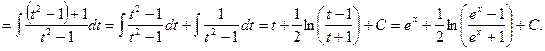
Проверка:
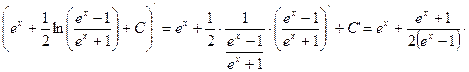
![]()
![]()
![]() – верно.
– верно.
___________________________________________________________________________
6) ![]() .
.
Решение:
![]()
![]()
Проверка:
 – верно.
– верно.
___________________________________________________________________________
7) ![]() .
.
Решение:
![]()
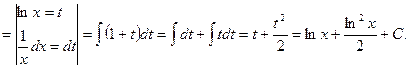
Проверка:
 – верно.
– верно.
___________________________________________________________________________
8) ![]()
Решение:
![]()
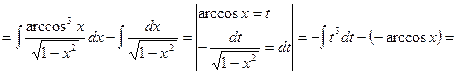
![]()
Проверка:
 – верно.
– верно.
__________________________________________________________________________________
9) ![]() .
.
Решение:
![]()
![]()
Проверка:
![]() – верно.
– верно.
___________________________________________________________________________
2. Найти неопределенные интегралы:
1) ![]() .
.
Решение:
![]()
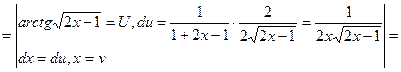
![]()
![]()
___________________________________________________________________________
2) ![]() .
.
Решение:
![]()
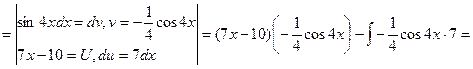
![]()
___________________________________________________________________________
3) ![]() .
.
Решение:
![]()
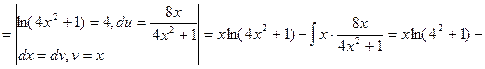
![]()
___________________________________________________________________________
4) ![]() .
.
Решение:
![]()
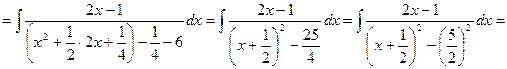
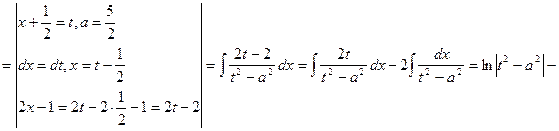
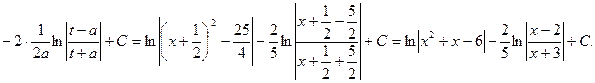
___________________________________________________________________________
5) ![]() .
.
Решение:
![]()
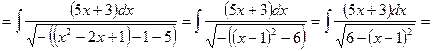
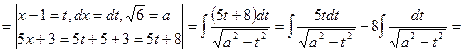
![]()
![]()
___________________________________________________________________________
6) ![]() .
.
Решение:
![]()
![]()
![]()
___________________________________________________________________________
7) ![]() .
.
Решение:
![]()
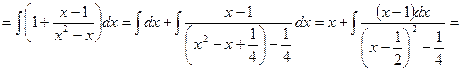
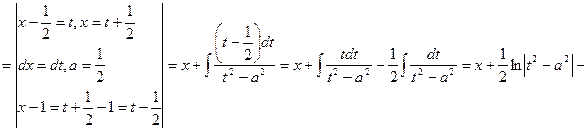

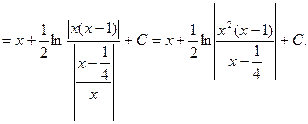
___________________________________________________________________________
8) ![]() .
.
Решение:
![]()
![]()
![]()
![]()
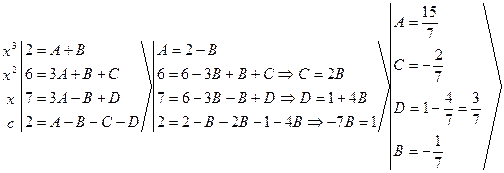
![]()
![]()
![]()
___________________________________________________________________________
9) ![]() .
.
Решение:
![]()
![]()
___________________________________________________________________________
10) ![]() .
.
Решение:
![]()
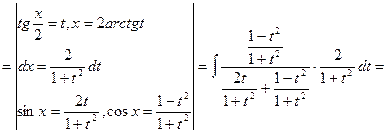
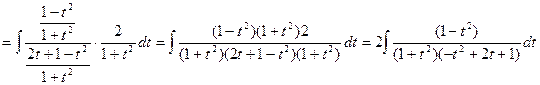
![]()
![]()
![]()
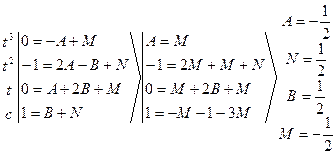
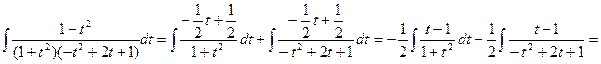
![]()
![]()
__________________________________________________________________________________
11) ![]() .
.
Решение:
![]()
___________________________________________________________________________
12) 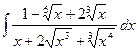 .
.
Решение:
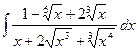
___________________________________________________________________________
13) ![]() .
.
Решение:
![]()
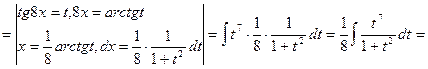
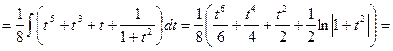
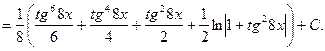
___________________________________________________________________________
14) 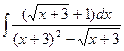 .
.
Решение:
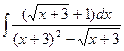
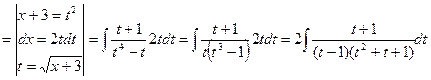
![]()
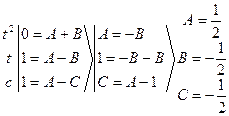
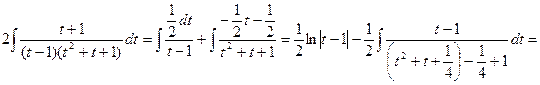
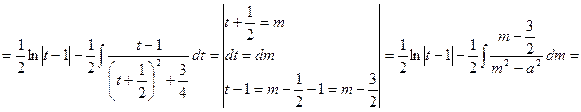
![]()
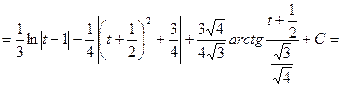
![]()
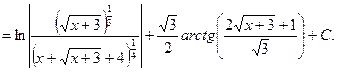
___________________________________________________________________________
15) ![]() .
.
Решение:
![]()
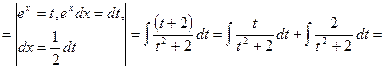
![]()
![]()
___________________________________________________________________________
3. Вычислить определенный интеграл:
1) 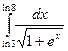 .
.
Решение:
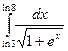
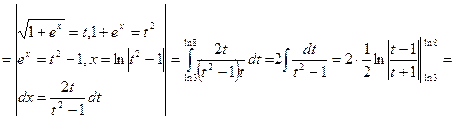
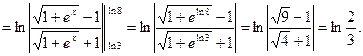
___________________________________________________________________________
2) ![]() .
.
Решение:
![]()
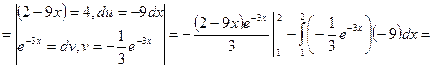
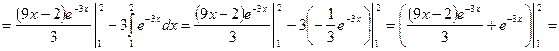
![]()
___________________________________________________________________________
3) 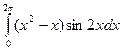 .
.
Решение:
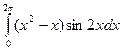
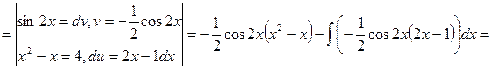
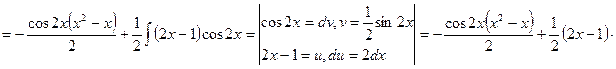
![]()
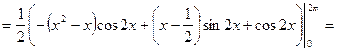
![]()
____________________________________________________________________________
4. Найти несобственные интегралы или доказать их расходимость:
1) ![]() .
.
Решение:
![]() – интеграл I рода.
– интеграл I рода.
![]()

![]()
![]() – сходящийся.
– сходящийся.
____________________________________________________________________________
2) 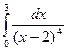 .
.
Решение:
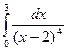 – интеграл II рода.
– интеграл II рода.
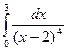
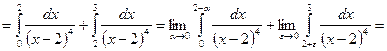
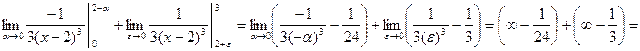
![]() – расходящийся.
– расходящийся.
____________________________________________________________________________
3) 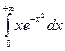 .
.
Решение:
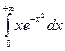
___________________________________________________________________________________
![]()






