Вероятностный смысл математического ожидания
Пусть проведено n испытаний, в которых случайная величина Х приняла 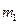 раз значение
раз значение  ,
, 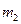 раз значение
раз значение 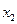 , … ,
, … , 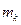 раз –
раз – 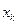 ,
, 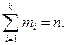 Тогда сумма всех значений, принятых Х равна
Тогда сумма всех значений, принятых Х равна 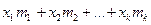 . Найдем среднее арифметическое
. Найдем среднее арифметическое 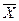 всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний n:
всех значений, принятых случайной величиной, для чего разделим найденную сумму на общее число испытаний n:
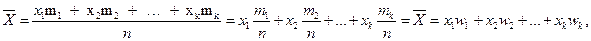 где
где 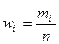 – относительная частота (частость).
– относительная частота (частость).
Допустим, что число испытаний достаточно велико, тогда 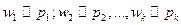 и
и 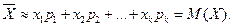
Таким образом, математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины.
Свойства М(Х)
1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С) = С, С = const.
С имеет одно значение, равное С,с вероятностью p = 1, М(С)=С . 1 = С.
Определим произведение постоянной С на Х как дискретную случайную величину 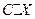 , возможные значения которой равны произведениям С на возможные значения Х. Вероятность
, возможные значения которой равны произведениям С на возможные значения Х. Вероятность 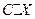 равна вероятностям Х. Например, если
равна вероятностям Х. Например, если  имеет вероятность
имеет вероятность 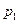 , то
, то 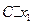 имеет также вероятность
имеет также вероятность 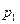 .
.
2. М(СХ) = С . М(Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величина X задана законом распределения:
Тогда 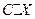 имеет закон распределения:
имеет закон распределения:
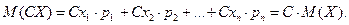
Случайные величины X и Y называют независимыми, если закон распределения одной из них не зависит от того, какие значения принимает другая.
Произведение 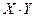 – случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятности XY равны произведению соответствующих вероятностей X и Y.
– случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятности XY равны произведению соответствующих вероятностей X и Y.
3. 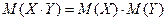 , где X, Y – независимые дискретные случайные величины.
, где X, Y – независимые дискретные случайные величины.
Пусть законы распределения вероятностей этих величин:
Составим значения, которые могут принимать 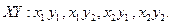 Закон распределения:
Закон распределения:
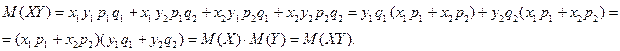
4. M(X Y) = M(X) M(Y).
Возможные значения случайной величины X Y равна сумме возможных значений X и Y , а вероятность X Y равна произведению вероятностей слагаемых.
Теорема. М(Х) числа появлений событий А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытании p.
Иначе, М(Х) биноминального распределения равно 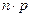 .
.
Дисперсия случайной дискретной величины и ее свойства
Легко указать случайные величины, имеющие одинаковые значения математических ожиданий, но различные возможные значения, например:
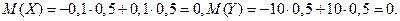
Х имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от М(Y), таким образом, М(Х) полностью не характеризует Х. Надо охарактеризовать отклонение случайной величины от M(X): отклонение – это величина X – M(X).
Теорема. Математическое ожидание отклонения равно нулю.
Действительно, 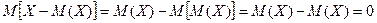 , поэтому для оценки отклонения берут квадрат отклонения.
, поэтому для оценки отклонения берут квадрат отклонения.
Дисперсией (рассеянием) дискретных случайных величин называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: 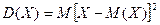 .
.
Получаем: 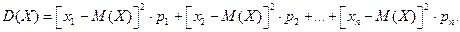
Пример. Найти 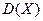 случайной величины:
случайной величины:
M(X) = 1 . 0,3 2 . 0,5 5 . 0,2 = 2,3. Найдем все возможные значения квадрата отклонения: 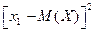 = (1 – 2,3)2 = 1,69;
= (1 – 2,3)2 = 1,69; 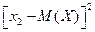 = (2 – 2,3)2 = 0,09;
= (2 – 2,3)2 = 0,09; 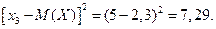
Напишем закон распределения квадрата отклонения:
Тогда (по определению): 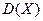 = 1,69 . 0,3 0,09 . 0,5 7,29 . 0,2 = 2,01.
= 1,69 . 0,3 0,09 . 0,5 7,29 . 0,2 = 2,01.
Удобнее: 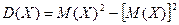 .
.
Доказательство:
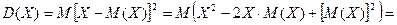
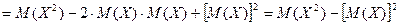 .
.
Вычислим дисперсию в предыдущем примере по доказанной формуле. Составим закон распределения 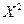 :
:
Тогда 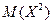 = 1 . 0,3 4 . 0,5 25 . 0,2 = 7,3. Найдем
= 1 . 0,3 4 . 0,5 25 . 0,2 = 7,3. Найдем 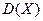 :
: 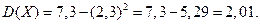
Свойства дисперсии
1. Дисперсия постоянной величины равной нулю. D(C) = 0.
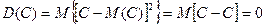 .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
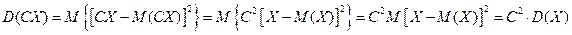 .
.
Если |C| > 1, то величина СХ имеет большие (по модулю) значения, поэтому D(CX)>D(X).
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин D(X Y) = D(X) D(Y). Докажем: 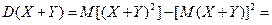
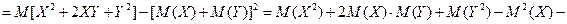

Следствие: D(X C) = D(X) D(C) = D(X), С = const.
4. D(X – Y) = D(X) D(Y). Докажем: D(X–Y) = D(X) D(–Y) = D(X) (–1)2D(X) = =D(X) D(Y).
Теорема. Дисперсия числа появлений событий А в n независимых испытаниях, в каждом из которых вероятность появления события А p = const, равна npq = D(X),где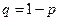 .
.
Иначе. Дисперсия биноминального распределения равна D(X)= npq.
§
Среднее квадратичное отклонение случайной величины Х – это корень квадратный из дисперсии: 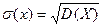 .
.
Размерность дисперсии равна квадрату размерности Х, тогда как размерность s(Х) равна размерности Х. Во многих случаях это оказывается удобнее.
Пусть 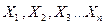 – независимые случайные величины, тогда
– независимые случайные величины, тогда 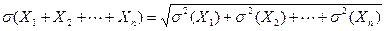 . По свойству дисперсии:
. По свойству дисперсии: 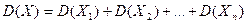 , тогда
, тогда 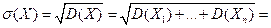
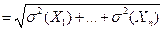 .
.
Начальные и центральные теоретические моменты
Начальным моментом порядка k случайной величины Х называют математическое ожидание величины 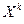 :
:  Например,
Например,  ,
, 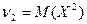 ,
,  ,…
,…
 .
.
Центральным моментом порядка k называется математическое ожидание величины 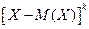 :
: 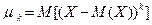 , например,
, например, 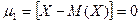 ,
, 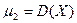 и т.д.
и т.д.
Мода и медиана. Модой случайной величины называется ее наиболее вероятное значение (для дискретных величин) или то значение, в котором плотность вероятности максимальна. Если имеется более одного максимума, то распределение называют полимодальным.
случайной величины называется ее наиболее вероятное значение (для дискретных величин) или то значение, в котором плотность вероятности максимальна. Если имеется более одного максимума, то распределение называют полимодальным.
Медианой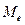 называют такое значение случайной величины (обычно – непрерывной), для которого
называют такое значение случайной величины (обычно – непрерывной), для которого 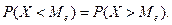 Геометрически – абсцисса точки, в которой площадь делится пополам.
Геометрически – абсцисса точки, в которой площадь делится пополам.
Функция распределения вероятностей случайной величины
Дискретная случайная величина может быть задана перечислением всех ее возможных значений и их вероятностей – законом распределения. Но его нельзя использовать для задания непрерывных случайных величин. Необходим общий способ задания случайных величин – это функция распределения вероятностей случайных величин.
Пусть x – действительное число. Вероятность того, что случайная величина Х примет значение, меньше x, т.е. Р(X<x) обозначим через F(x). Если x изменяется, то изменяется и F(x), т.е. F(x) – функция х.
Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньше x, т.е. F(x)=P(X<x). Геометрически F(x) есть вероятность того, что случайная величина примет значение, которое изображается точкой левее точки х.
Добавим более четкое определение непрерывной случайной величины – случайная величина называется непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Свойства F(x)
1. Значения функции распределения принадлежат отрезку [0;1], т.е. 0 £ F(x)£ 1 – F(x) вероятность, 0 £ P(A) £ 1 .
2. F(x) неубывающая функция, т.е. F( 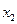 ) ³ F(
) ³ F(  ), если
), если 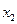 >
>  .
.
Доказательство:
Пусть 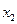 >
>  . Событие, состоящее в том, что Х примет значение меньше
. Событие, состоящее в том, что Х примет значение меньше 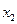 , можно разделить на 2 несовместных события:
, можно разделить на 2 несовместных события:
1. Х примет значение, меньше  , с вероятностью Р(
, с вероятностью Р(  <
< );
);
2. Х примет значение  £
£  <
< 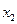 с вероятностью P(
с вероятностью P( £
£  <
< 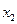 ).
).
По теореме сложения: Р( <
< 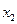 ) = Р(
) = Р( < x1) P(
< x1) P( £
£  <
< 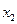 ),
),
отсюда Р( <
< 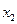 ) – Р(
) – Р( <
<  ) = P(
) = P( £
£  < x2) или F(
< x2) или F(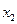 ) – F(
) – F( ) = P(
) = P( £
£  <
< 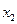 ), но
), но 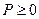 .
.
Следствие 1. Вероятность того, что 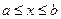 равна приращению F(x) на этом интервале: Р(
равна приращению F(x) на этом интервале: Р( 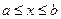 ) = F(b) – F(a) (
) = F(b) – F(a) (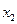 =b, x1=a).
=b, x1=a).
Следствие 2. Вероятность того, что случайная величина Х примет одно определенное значение равна 0.
Р(a £ Х < b) = Р(a < Х < b) = Р(a < x £ b) = Р(a £ x £ b).
3. Если возможные значения случайной величины Î (a,b), то: 1) F(x)= 0 при x £ a;
2) F(x) = 1 при x >b.
Докажем. Если  £ a, то события X<x невозможны. Пусть
£ a, то события X<x невозможны. Пусть 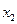 ³ b, тогда X<
³ b, тогда X< 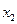 – достоверное событие.
– достоверное событие.
Следствие. Если значения непрерывной случайной величины расположены на всей числовой оси, то 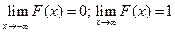 .
.
Плотность распределения вероятностей непрерывной
Случайной величины
Непрерывную случайную величину можно задать функцией распределения, однако можно использовать и плотностью распределения.
Плотностью распределения вероятностей непрерывной случайной величины Х называют производную от функции распределения: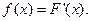
Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равно 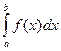 , т.е. Р(a < Х < b) =
, т.е. Р(a < Х < b) = 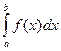 .
.
Доказательство:
Если известна функция распределения, то Р(a £ X £ b) = F(b) – F(a). По формуле Ньютона-Лейбница: F(b) – F(a) = 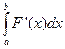 =
= 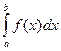 , а Р(a £ X £ b) = Р(a < X < b).
, а Р(a £ X £ b) = Р(a < X < b).
Пример. Дана плотность вероятности:
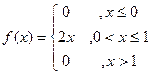 .
.
Найти вероятность того, что в результате испытания Х примет значение Î (0,5; 1).
Р(0,5 < X < 1) = 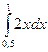 = 0,75.
= 0,75.
Функцию распределения можно найти по плотности распределения: F(x) = 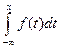 . Действительно, F(x) = P(X<x) или F(x) = P(–¥ < X < x), тогда
. Действительно, F(x) = P(X<x) или F(x) = P(–¥ < X < x), тогда  .
.
По известной функции распределения можно найти плотность: 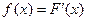 .
.
Пример. Найти F(x), если 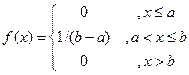 .
.
Если x £ a, f(x) = 0, то  , если
, если 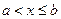 :
: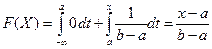 . Если
. Если 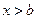 , то
, то 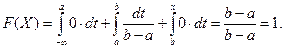
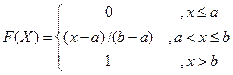 .
.
Свойства f(x)
1 . f(x) ³ 0, т.к. F(x) – неубывающая функция, поэтому, 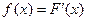 ³ 0.
³ 0.
2. 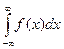 =1. Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение
=1. Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение 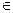 (–µ;µ) – достоверное событие, поэтому р = 1.
(–µ;µ) – достоверное событие, поэтому р = 1.
Вероятностный смысл 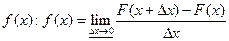 , тогда:
, тогда:
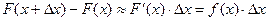 – вероятность того, что случайная величина примет значение
– вероятность того, что случайная величина примет значение 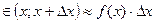 .
.
§
Неравенство Чебышева. Вероятность того, что отклонение случайной величины от ее математического ожидания по модулю меньше числа 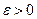 , не меньше, чем
, не меньше, чем 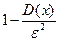 , т.е.
, т.е. 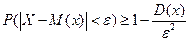 .
.
Рассмотрим дискретную случайную величину X, имеющую закон распределения:
Закон распределения случайной величины 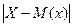 :
:
Предположим, что первые k значений случайной величины 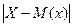 меньше данного
меньше данного 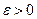 , а остальные – не меньше
, а остальные – не меньше 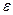 . Тогда
. Тогда 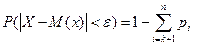 . Запишем формулу для дисперсии в виде:
. Запишем формулу для дисперсии в виде: 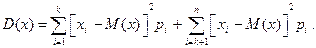 Отбросим первое слагаемое и во втором слагаемом заменим
Отбросим первое слагаемое и во втором слагаемом заменим 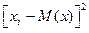 меньшей величиной
меньшей величиной 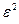 , получим
, получим 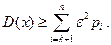 Отсюда:
Отсюда: 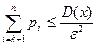 , т.е.
, т.е. 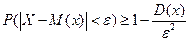 . Иначе:
. Иначе: 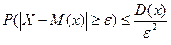 . Для частости:
. Для частости:  .
.
Теорема Чебышева. Если 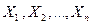 – попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было
– попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было 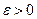 , вероятность неравенства
, вероятность неравенства 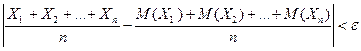 будет как угодно близка к единице, если число случайных величин достаточно велико, т.е.
будет как угодно близка к единице, если число случайных величин достаточно велико, т.е. 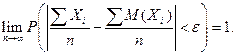
Рассмотрим случайную величину 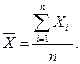 Имеем:
Имеем: 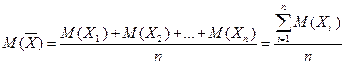 ;
; 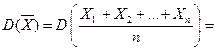
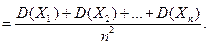 По условию теоремы дисперсия ограничена, т.е.
По условию теоремы дисперсия ограничена, т.е. 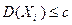 , поэтому
, поэтому 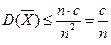 . Воспользуемся неравенством Чебышева:
. Воспользуемся неравенством Чебышева: 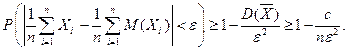 Перейдя к пределу и учитывая, что
Перейдя к пределу и учитывая, что 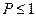 , получим доказываемое.
, получим доказываемое.
Теорема Бернулли
Пусть в каждом из n независимых испытаний вероятность p появления события А постоянна. Тогда как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Или  , где
, где 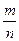 – частота появления события A.
– частота появления события A.
Пусть 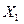 – число появлений события A в первом испытании,
– число появлений события A в первом испытании, 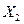 – во втором,
– во втором,  – в n-ом испытании,
– в n-ом испытании, 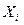 может принимать значения : 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью
может принимать значения : 1 (событие А наступило) с вероятность р и 0 (событие А не наступило) с вероятностью 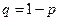 . Испытания независимые,
. Испытания независимые, 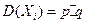 , так как
, так как 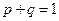 , то
, то 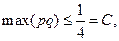
 , тогда по неравенству Чебышева:
, тогда по неравенству Чебышева: 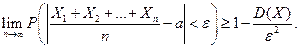
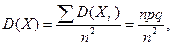
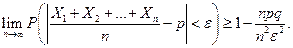 Каждая величина
Каждая величина 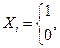 тогда
тогда 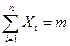 – числу появления события А в n испытаниях, тогда
– числу появления события А в n испытаниях, тогда 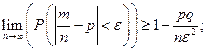 следовательно,
следовательно,  .
.
Теорема Пуассона. Если в последовательности n независимых испытаний вероятность появления события А в каждом испытании равна 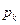 , то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей
, то при увеличении n частость события A сходится (по вероятности) к среднему арифметическому вероятностей 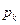 , т.е.
, т.е. 
Пусть случайная величина 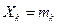 – число появлений события А в каждом испытании, тогда
– число появлений события А в каждом испытании, тогда 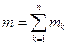 – число появлений события А в n испытаниях.
– число появлений события А в n испытаниях. 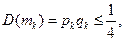
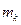 – независимые величины. Для случайной величины
– независимые величины. Для случайной величины 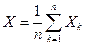 имеем:
имеем: 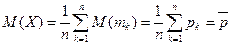 среднее арифметическое вероятностей;
среднее арифметическое вероятностей; 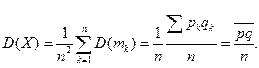 Тогда по неравенству Чебышева:
Тогда по неравенству Чебышева: 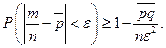 Переходя к пределу, получим доказываемое.
Переходя к пределу, получим доказываемое.
Функция одного случайного аргумента и ее распределение
Если каждому возможному значения случайной величины Х соответствует одно возможное значение случайной величины Y, то Y – функция от X: Y=j(X).
Найдем закон распределения вероятностей функции по известному распределению дискретного и непрерывного аргумента.
1) Если X – дискретная величина. Найти распределение Y=X2. Вероятности соответствующих значений X и Y равны:
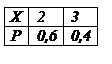
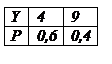
2) Пусть X – непрерывная случайная величина.
Пусть Y=j(X) и плотность распределения f(x) известна, тогда 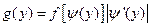 , где
, где 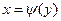 – обратная функция для функции у=j(х), которая должна быть дифференцируемой и строго возрастающей или убывающей функцией.
– обратная функция для функции у=j(х), которая должна быть дифференцируемой и строго возрастающей или убывающей функцией.
Математическое ожидание функции одного случайного аргумента
Пусть Y=j(X) – функция случайного аргумента Х. Найдем M(Y).
Пусть Х дискретная случайная величина: 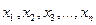 с вероятностью
с вероятностью 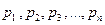 , Y – тоже дискретная случайная величина со значениями:
, Y – тоже дискретная случайная величина со значениями: 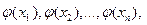 с вероятностью
с вероятностью 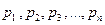 . Тогда
. Тогда 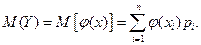
Пусть X – непрерывная случайная величина, заданная плотностью f(x).
а) можно найти g(y) – плотность распределения величины Y и 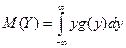 , однако проще:
, однако проще: 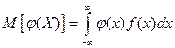 .
.
Закон распределения вероятностей и функция распределения двумерных случайных величин
До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом – одномерные. Кроме одномерных случайных величин изучают величины, возможные значения которых определяются 2, 3,…, n числами. Такие величины называются двумерными, трехмерными, …, n-мерными.
Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X, Y называют компонентами (составляющими); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Пример: станок штампует плитки. Если контролировать длину X и ширину Y – то имеем двухмерную случайную величину (X, Y).
§
Закон распределения дискретной двумерной случайной величины – перечень возможных значений этой величины, т.е. пары чисел 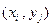 и их вероятностей
и их вероятностей 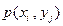
 .
.
События (Х= 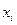 ,
, 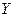 =
= 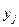 )
) 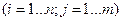 образуют полную группу, поэтому сумма вероятностей, помещенных в таблице, равна 1. Можно найти законы распределения каждой составляющей. События (Х=
образуют полную группу, поэтому сумма вероятностей, помещенных в таблице, равна 1. Можно найти законы распределения каждой составляющей. События (Х=  ,
, 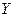 =
=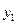 ), (Х=
), (Х=  ,
, 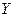 =
=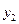 ),…,(Х=
),…,(Х=  ,
, 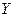 =
=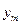 ) несовместны, поэтому
) несовместны, поэтому  – вероятность того, что Х примет значение
– вероятность того, что Х примет значение  равно сумме вероятностей «столбца
равно сумме вероятностей «столбца  ».
».  – просуммировать вероятности «столбца
– просуммировать вероятности «столбца  ». Аналогично,
». Аналогично, 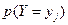 равно сумме вероятности строки
равно сумме вероятности строки 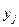 .
.
Функции распределения двумерной случайной величины
Функцией распределения двумерной случайной величины (X, Y) называют 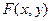 , определяющую вероятность того, что X<x, Y<y: F(x,y)=P(X<x, Y<y).
, определяющую вероятность того, что X<x, Y<y: F(x,y)=P(X<x, Y<y).
Свойства:
1. 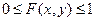 – вероятность.
– вероятность.
2. 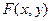 – неубывающая функция по каждому аргументу, т.е.
– неубывающая функция по каждому аргументу, т.е. 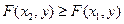 , если
, если 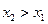 ;
; 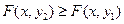 если
если 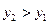 .
.
3. Предельные соотношения: 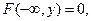
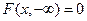 ,
, 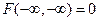 ,
, 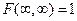 .
.
4.  ,
, 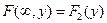 .
.
При 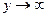 функция распределения системы
функция распределения системы 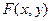 становится функцией распределения составляющей Х; при
становится функцией распределения составляющей Х; при 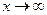 функция распределения системы становится функцией распределения составляющей Y.
функция распределения системы становится функцией распределения составляющей Y.
Вероятность попадания случайной величины в полуполосу
И прямоугольник
Найдем вероятность того, что в результате испытания случайная точка попадет в полуполосу: 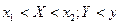 или в полуполосу
или в полуполосу 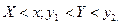
Функция распределения 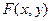 считается известной, она определяет вероятность попадания случайной точки в квадрант с вершиной
считается известной, она определяет вероятность попадания случайной точки в квадрант с вершиной 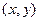 . Тогда вероятность попадания случайной точки в полуполосу равна:
. Тогда вероятность попадания случайной точки в полуполосу равна: 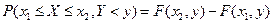 – это разность вероятностей попадания случайной точки в квадрант с вершиной
– это разность вероятностей попадания случайной точки в квадрант с вершиной 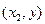 и вероятности попадания случайной точки в квадрант с вершиной
и вероятности попадания случайной точки в квадрант с вершиной 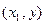 . Аналогично,
. Аналогично, 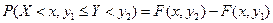 . Вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
. Вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.
Рассмотрим вероятность попадания в прямоугольник ABCD, заданий уравнениями сторон: 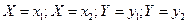 . Эта вероятность равна разности вероятности попадания случайной точки в полуполосу АВ и вероятность попадания случайной точки в полуполосу CD:
. Эта вероятность равна разности вероятности попадания случайной точки в полуполосу АВ и вероятность попадания случайной точки в полуполосу CD: 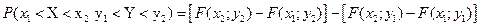 .
.
 Y
Y







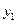



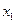
 X
X
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
Непрерывную двумерную случайную величину можно также задать, пользуясь плотностью распределения. Будем предполагать, что функция распределения 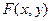 всюду непрерывна и имеет непрерывную частную производную второго порядка.
всюду непрерывна и имеет непрерывную частную производную второго порядка.
Двумерная плотность распределения вероятностей – вторая смешанная частная производная от функции 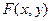 :
: 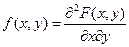 .
.
Геометрически – это поверхность (поверхность распределения). Зная плотность распределения 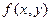 , можно найти функцию распределения
, можно найти функцию распределения 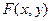 :
: 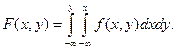
Вероятностный смысл f(x, y)
Вероятность попадания случайной точки в прямоугольник ABCD:  . Применим теорему Лагранжа:
. Применим теорему Лагранжа: 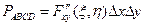 , где
, где 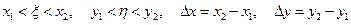 . Отсюда
. Отсюда 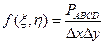 – это отношение вероятности попадания в квадрат к его площади.
– это отношение вероятности попадания в квадрат к его площади.
Перейдем к пределу 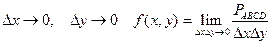 .
.
Свойства 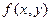 :
:
1) f(x,y)³0 (F(x,y), поскольку 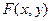 – неубывающая функция своих аргументов.
– неубывающая функция своих аргументов.
2) 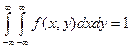 .
.
Вероятность попадания случайной точки в произвольную область
 – это вероятность попадания случайной точки в прямоугольник со сторонами
– это вероятность попадания случайной точки в прямоугольник со сторонами  и
и 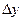 . Разобьем область D на n элементарных областей прямыми, параллельными Оу и Ох на расстоянии Dх и Dу. Вероятность попадания случайной точки в область D равна сумме вероятностей попадания точки в элементарные области:
. Разобьем область D на n элементарных областей прямыми, параллельными Оу и Ох на расстоянии Dх и Dу. Вероятность попадания случайной точки в область D равна сумме вероятностей попадания точки в элементарные области: 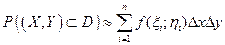 . Переходя к пределу, получим
. Переходя к пределу, получим 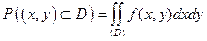 .
.
Раздел IX. Элементы математической статистики
Глава 23. Статическая оценка параметров распределения
Задачи математической статистики. Вариационный ряд
Первая задача статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или экспериментов.
Вторая задача – разработать методы анализа статистических данных в зависимости от целей исследования:
а) оценка неизвестной вероятности события, известной функции распределения, параметров распределения, вид которого известен и т.д.
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Для исследования какого-либо признака из генеральной совокупности (всех объектов) извлекают выборку – случайно отображенные объекты.
Вариационный ряд
Рассмотрим пример. Токарь изготавливал в течение 10 дней следующее количество деталей: 5,6,5,7,7,7,8,5,6,5. Ранжируем эту выборку – разобьем на группы:
5,5,5,5 6,6 7,7,7 8
4 раза 2 раза 3 раза 1 раз.
При ранжировании группы располагаются в порядке возрастания. Значение каждой группы называется вариантой. Число повторений в каждой группе называется частотой варианты. Полученную таблицу называют вариационным рядом.
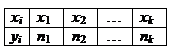
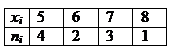
В общем виде:
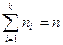 – объем выборки.
– объем выборки.
Графическое изображение вариационного ряда – полигон.
Для непрерывного признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-й интервал.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны 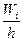 , где
, где 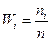 – относительная частота.
– относительная частота.
Точечные оценки
Вариационный ряд характеризует случайную величину, но не в полной мере, поэтому используются характеристики, аналогичные теоретическим – М(х), D(х) и т.д. Эти числовые характеристики подсчитываются на основании выборки и называются точечными оценками (т.к. являются числами).
Точечной оценкой характеристики Q называется некоторая функция Q* результатов наблюдений, значение которой принимают за приближение этой характеристики: 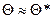 . Качество точечной оценки определяется характеристиками:
. Качество точечной оценки определяется характеристиками:
1. Несмещенность оценки: точечная оценка называется несмещенной, если ее математическое ожидание равно оценивающему параметру: 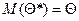 , т.е. совпадает с истинным значением.
, т.е. совпадает с истинным значением.
2. Состоятельность: точечная оценка называется состоятельной, если она при 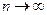 стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру.
3. Эффективность: точечная оценка считается эффективной, если она имеет (при заданном n) наименьшую дисперсию.
Основные точечные оценки
- Выборочная средняя:
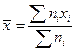 .
.
Выборочная средняя 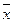 приближается к М(х), является несмещенной, состоятельной и эффективной.
приближается к М(х), является несмещенной, состоятельной и эффективной.
2. Выборочная дисперсия: 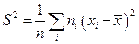 . S2 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию:
. S2 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию: 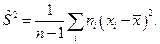
3. Начальные и центральные моменты k– го порядка. Начальный момент k-го порядка: 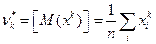 . Центральный момент k-го порядка:
. Центральный момент k-го порядка: 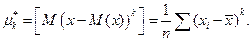
§
При выборке малого объема точечная оценка может сильно отличаться от оцениваемого параметра, поэтому широко используют интервальные оценки. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Доверительной вероятностью (надежностью) называется вероятность g, с которой осуществляется неравенство 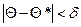 , т.е.
, т.е. 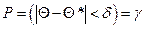 , где Q* – найденная характеристика параметра Q. Надежность g обычно выбирается 0,95; 0,99; 0,999 и т.д.
, где Q* – найденная характеристика параметра Q. Надежность g обычно выбирается 0,95; 0,99; 0,999 и т.д.
Интервальные оценки для генеральной средней с известным s
Пусть известно среднее квадратическое отклонение s генеральной совокупности с нормальным законом распределения. Требуется оценить неизвестное математическое ожидание а по выборочной средней 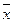 . Будем рассматривать выборочную среднюю
. Будем рассматривать выборочную среднюю 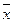 как случайную величину
как случайную величину 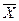 , для которой
, для которой 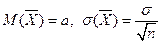 (
( 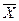 – случайная величина, т.к.
– случайная величина, т.к. 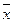 меняется от выборки к выборке).
меняется от выборки к выборке).
Тогда по следствию интегральной теоремы Лапласа имеем:  , где
, где 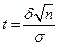 ,
, 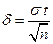 – точность оценки.
– точность оценки.
Число 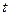 определяем по таблице значений функции Лапласа:
определяем по таблице значений функции Лапласа: 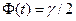 . Получаем:
. Получаем: 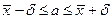 ,
, 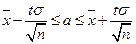 – интервальная оценка для математического ожидания а.
– интервальная оценка для математического ожидания а.
Пример. Случайная величина 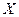 имеет нормальное распределение с s =3. Найти доверительный интервал для оценки генеральной средней а, если
имеет нормальное распределение с s =3. Найти доверительный интервал для оценки генеральной средней а, если 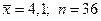 , надежность g = 0,95.
, надежность g = 0,95.
Найдем t: функция Лапласа 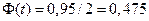 ,
, 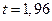 , точность:
, точность: 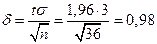 ,
, 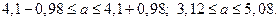
Интервальная оценка для генеральной средней с неизвестным s
Пусть признак Х генеральной совокупности распределен нормально, причем среднее квадратическое отклонение s неизвестно. Требуется оценить неизвестное математическое ожидание а по выборочной средней 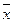 . Для построения интервальной оценки используется статистика
. Для построения интервальной оценки используется статистика 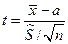 , имеющая распределение Стьюдента с числом степеней свободы
, имеющая распределение Стьюдента с числом степеней свободы 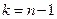 . Получаем:
. Получаем: 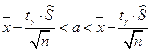 где n – объем выборки,
где n – объем выборки, 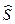 –исправленное среднее квадратическое отклонение,
–исправленное среднее квадратическое отклонение,  – выборочная средняя,
– выборочная средняя, 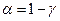 – уровень значимости,
– уровень значимости, 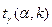 находим по распределению Стьюдента (t – распределение) (для двухсторонней критической области). Точность оценки:
находим по распределению Стьюдента (t – распределение) (для двухсторонней критической области). Точность оценки:  . Можно по таблице приложения 3 Гмурмана.
. Можно по таблице приложения 3 Гмурмана.
Пример. Средняя урожайность пшеницы на 16 опытных участках 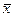 =25 ц/га, а
=25 ц/га, а 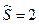 ц/га. Найти с надежностью 0,9 границы доверительного интервала для оценки генеральной средней.
ц/га. Найти с надежностью 0,9 границы доверительного интервала для оценки генеральной средней.
Число степеней свободы 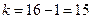 ,
, 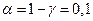 , по таблице распределения Стьюдента находим:
, по таблице распределения Стьюдента находим: 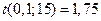 . Точность оценки:
. Точность оценки: 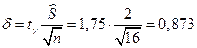 ; тогда
; тогда 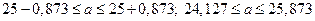 (ц/га).
(ц/га).
Интервальные оценки для генеральной дисперсии, среднего квадратического отклонения и генеральной доли
Пусть из генеральной совокупности, распределенной по нормальному закону 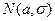 , взята выборка объема n и вычислена исправленная выборочная дисперсия
, взята выборка объема n и вычислена исправленная выборочная дисперсия  . Требуется определить с надежностью g интервальные оценки для s 2 и s.
. Требуется определить с надежностью g интервальные оценки для s 2 и s.
Случайная величина 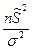 имеет распределение Пирсона (
имеет распределение Пирсона (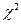 )с
)с 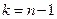 степенями свободы. Имеем:
степенями свободы. Имеем: 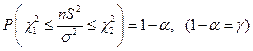 .
.
По таблице 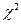 – распределения нужно выбрать такие
– распределения нужно выбрать такие 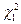 и
и  , чтобы площадь, заключенная под графиком плотности распределения
, чтобы площадь, заключенная под графиком плотности распределения 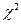 между
между 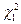 и
и  , была равна
, была равна 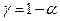 . Обычно:
. Обычно: 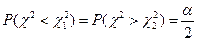 .
.
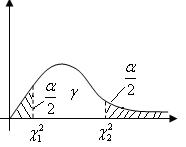
Тогда: 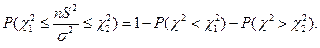 Поскольку таблица содержит лишь
Поскольку таблица содержит лишь 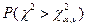 , то
, то 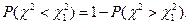 тогда из
тогда из 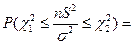
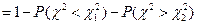 :
: 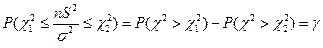 , т.е.
, т.е. 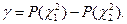 Эта формула используется при решении обратной задачи – нахождение доверительной вероятности по заданному доверительному интервалу генеральной дисперсии.
Эта формула используется при решении обратной задачи – нахождение доверительной вероятности по заданному доверительному интервалу генеральной дисперсии. 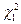 и
и  находим из равенств:
находим из равенств:  Запишем неравенство из
Запишем неравенство из 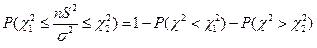 :
: 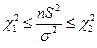 и преобразуем его:
и преобразуем его:  .
.
Если 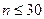 , то доверительный интервал для s:
, то доверительный интервал для s: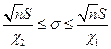 . Если
. Если 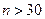 , то
, то 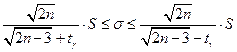 , где
, где 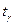 определяется по таблице функции Лапласа:
определяется по таблице функции Лапласа: 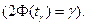
Можно по упрощенной формуле (Гмурман):  , где параметр
, где параметр 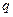 находят по таблице приложения 4 (Гмурман) по заданным n и g.
находят по таблице приложения 4 (Гмурман) по заданным n и g.
Пример. По результатам контроля n = 9 деталей вычислено 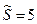 мм. В предположении, что ошибка распределена нормально, определить при g = 0,95 доверительный интервал для s.
мм. В предположении, что ошибка распределена нормально, определить при g = 0,95 доверительный интервал для s.
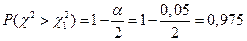 ;
; 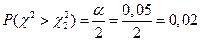 .
.
По таблице 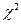 для
для  ,
, 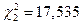 ,
,  (мм).
(мм).
Интервальная оценка для генеральной доли
Пусть в n независимых испытаниях событие А, вероятность появления которого равна р, имело место m раз (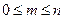 ), тогда границы доверительного интервала для генеральной доли:
), тогда границы доверительного интервала для генеральной доли:  , где
, где 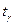 определяется по таблице Лапласа:
определяется по таблице Лапласа: 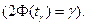
Пример. При испытании зерна на всхожесть из 400 зерен проросло 384. С надежностью g = 0,98 определить доверительный интервал для генеральной доли р.
 ,
,  (Лаплас),
(Лаплас), 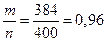 , точность оценки:
, точность оценки: 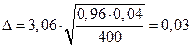 ;
; 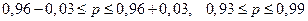 .
.
Глава 24. Статистическая проверка статистических гипотез
§
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.
Нулевой (основной) называют выдвинутую гипотезу 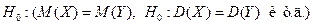 .
.
Конкурирующей называют гипотезу Н1, которая противоречит нулевой. Если выдвинутая гипотеза будет отвергнута, то имеет место конкурирующая гипотеза.
Выдвинутая гипотеза может быть правильной или неправильной, т.е. ее необходимо проверять. В итоге статистической проверки гипотез в двух случаях может быть принято неправильное решение:
– ошибка 1 рода – будет отвергнута правильная гипотеза;
– ошибка 2 рода – будет принята неправильная гипотеза.
Для проверки статистической гипотезы используют статистический критерий, т.е. правило, устанавливающее условия, при которых проверяемую гипотезу следует либо принять, либо отвергнуть. Основу критерия составляет специальная случайная величина (статистика) K с известным законом распределения. Задаваясь уровнем значимости 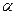 , т.е. вероятностью совершить ошибку 1 рода, критерий позволяет разбить все множество значений статистики на 2 непересекающихся подмножества: область принятия гипотезы и критическую область (область отклонения гипотезы).
, т.е. вероятностью совершить ошибку 1 рода, критерий позволяет разбить все множество значений статистики на 2 непересекающихся подмножества: область принятия гипотезы и критическую область (область отклонения гипотезы).
Основной принцип проверки гипотезы: если значение статистики, рассчитанное для выборки, попадает в критическую область, то гипотезу отвергают, в противном случае – гипотезу принимают. В зависимости от вида конкурирующей гипотезы Н1выбирают:
1. правостороннюю критическую область 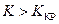 . Критическое значение статистики
. Критическое значение статистики 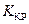 вычисляем из условия
вычисляем из условия 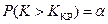 .
.
2. левостороннюю критическую область: 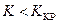 ,
, 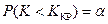 .
.
3. двухсторонняя критическая область: 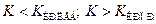 Обычно считают, что
Обычно считают, что 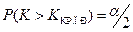 ,
, 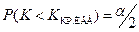 и если критические точки симметричны относительно нуля, то
и если критические точки симметричны относительно нуля, то  .
.
Схема проверки гипотез
1. По условию задачи формулируют основную 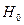 и конкурирующую гипотезы.
и конкурирующую гипотезы.
2. Задают величину уровня значимости a: 0,05; 0,01; 0,001.
3. Выбирают статистику, определяющую критерии проверки и выясняют ее закон распределения.
4. С помощью закона распределения статистики определяют 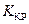 при уровне значимости a (т.е. границы критической области).
при уровне значимости a (т.е. границы критической области).
5. По результатам выборки вычисляют значение статистики 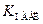 . Если
. Если 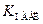 попадает в критическую область, то гипотезу отвергают, если нет – принимают.
попадает в критическую область, то гипотезу отвергают, если нет – принимают.
24.2. Проверка гипотезы о равенстве двух дисперсий нормальных генеральных совокупностей
Этот вопрос возникает, если требуется сравнить точности приборов, методов измерений и т.д.
Пусть Х и Y – нормально распределенные генеральные совокупности. По двум выборкам объемами n1 и n2 найдены исправленные выборочные дисперсии 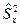 и
и 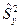 . При уровне значимости a проверяем нулевую гипотезу
. При уровне значимости a проверяем нулевую гипотезу 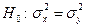 ,
, 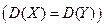 при конкурирующей гипотезе
при конкурирующей гипотезе  .
.
Исправленные выборочные дисперсии обычно различные. Требуется установить: различие значимо (существенно) или незначимо, т.е. объясняется случайными причинами. Выбираем F – статистику, распределенную по закону Фишера–Снедекора. Наблюдаемое значение: 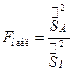 (отношение большой исправленной дисперсии к меньшей), число степеней свободы:
(отношение большой исправленной дисперсии к меньшей), число степеней свободы: 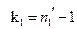 (где
(где 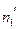 – объем выборки с большей исправленной дисперсией),
– объем выборки с большей исправленной дисперсией), 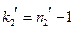 (где
(где 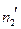 – объем выборки с меньшей исправленной дисперсией). По таблице критических точек распределения Фишера–Снедекора для уровня значимости a, числа степеней свободы
– объем выборки с меньшей исправленной дисперсией). По таблице критических точек распределения Фишера–Снедекора для уровня значимости a, числа степеней свободы  определяем
определяем 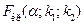 . Если
. Если 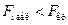 , то гипотеза принимается, если
, то гипотеза принимается, если 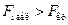 , то гипотеза отвергается.
, то гипотеза отвергается.
Если Н1 :  , то значение
, то значение 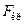 определяется для уровня значимости
определяется для уровня значимости 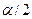 , поскольку необходимо построить двухстороннюю критическую область
, поскольку необходимо построить двухстороннюю критическую область  и
и  .
.
Иногда требуется проверить нулевую гипотезу  – определенное заданное значение генеральной дисперсии. Для проверки используют статистику
– определенное заданное значение генеральной дисперсии. Для проверки используют статистику 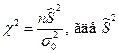 – исправленная выборочная дисперсия. Определяют
– исправленная выборочная дисперсия. Определяют 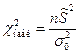 .
.
а) Если конкурирующая гипотеза имеет вид 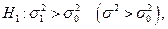 то для определения
то для определения 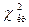 выбираем правостороннюю критическую область и по таблице распределения Пирсона (
выбираем правостороннюю критическую область и по таблице распределения Пирсона ( 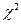 ) определяем
) определяем 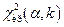 (на уровне значимости
(на уровне значимости 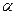 для числа степеней свободы
для числа степеней свободы 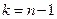 ). Если
). Если 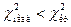 , то гипотезу
, то гипотезу 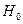 принимаем, если
принимаем, если 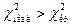 – отвергаем гипотезу
– отвергаем гипотезу 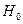 .
.
б) если 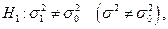 то строим двухстороннюю область, определяем левую
то строим двухстороннюю область, определяем левую 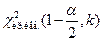 и правую
и правую 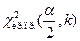 критические точки. Если
критические точки. Если 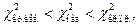 то гипотеза
то гипотеза 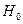 принимается, если
принимается, если 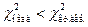 или
или 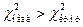 , то гипотеза
, то гипотеза 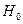 отвергается.
отвергается.
в) Если 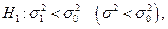 то строим левостороннюю критическую область, находим
то строим левостороннюю критическую область, находим 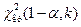 . Если
. Если 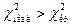 , то принимаем гипотезу
, то принимаем гипотезу 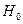 , если
, если 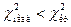 , то
, то 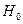 отвергается.
отвергается.
Пример. По 2 выборкам объемами n1 = 10 и n2 = 18 найдены исправленные выборочные дисперсии 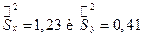 . При уровне значимости
. При уровне значимости 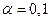 проверить гипотезу:
проверить гипотезу: 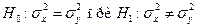 .
.
Находим 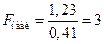 . Критическая область – двухсторонняя.
. Критическая область – двухсторонняя. 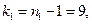
 ,
, 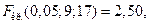 поскольку 3 > 2,5, то гипотеза отвергается (дисперсии различаются значимо).
поскольку 3 > 2,5, то гипотеза отвергается (дисперсии различаются значимо).
Закон распределения дискретной случайной величины
– этосоответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».А теперь очень важный момент: поскольку случайная величина ![]() обязательно примет одно из значений
обязательно примет одно из значений![]() полную группу и сумма вероятностей их наступления равна единице:
полную группу и сумма вероятностей их наступления равна единице:![]()
![]()
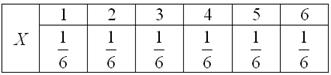
Без комментариев.
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
Пример 1
Некоторая игра имеет следующий закон распределения выигрыша: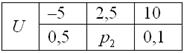
![]()
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина ![]() полную группу, а значит, сумма их вероятностей равна единице:
полную группу, а значит, сумма их вероятностей равна единице:![]()
![]()
![]()
![]()
![]() Ответ:
Ответ: ![]()
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
Пример 2
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины ![]() Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно ![]() классическому определению:
классическому определению:![]()
![]()
![]()
![]()
![]()
![]() Ответ: искомый закон распределения выигрыша:
Ответ: искомый закон распределения выигрыша:![]()
Следующее задание для самостоятельного решения:
Пример 3
Вероятность того, что стрелок поразит мишень, равна ![]()
![]()
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина ![]()
![]()
![]()
![]() сумме произведений всех её значений на соответствующие вероятности:или в свёрнутом виде:
сумме произведений всех её значений на соответствующие вероятности:или в свёрнутом виде:![]()
![]()
![]()
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру: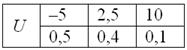
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
![]() проигрышно.
проигрышно.
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Пример 4
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины ![]() в среднем проигрывает игрок с каждой поставленной сотни?
в среднем проигрывает игрок с каждой поставленной сотни?
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
Пример 5
Случайная величина ![]()
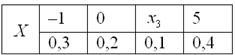
![]()
![]()
Есть?
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
Решения и ответы:
Пример 3. Решение: по условию ![]() – вероятность попадания в мишень. Тогда:
– вероятность попадания в мишень. Тогда:![]() – вероятность промаха.Составим
– вероятность промаха.Составим ![]() – закон распределения попаданий при двух выстрелах:
– закон распределения попаданий при двух выстрелах:![]() – ни одного попадания. По теореме умножения вероятностей независимых событий:
– ни одного попадания. По теореме умножения вероятностей независимых событий:![]()
![]() – одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:
– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:![]()
![]() – два попадания. По теореме умножения вероятностей независимых событий:
– два попадания. По теореме умножения вероятностей независимых событий:![]()
Проверка: 0,09 0,42 0,49 = 1
Ответ: ![]() Примечание: можно было использовать обозначения
Примечание: можно было использовать обозначения ![]() – это не принципиально.Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид:
– это не принципиально.Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: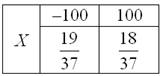
Вычислим математическое ожидание:![]()
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.Пример 5. Решение: по определению математического ожидания:![]()
поменяем части местами и проведём упрощения: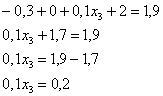
таким образом:![]() Выполним проверку:
Выполним проверку:![]()
![]() , что и требовалось проверить.Ответ:
, что и требовалось проверить.Ответ: ![]()
Пример 1
Производится
3 выстрела с вероятностями попадания в цель, равными p1=0,4; p2=0,3 и p3=0,6. Найти математическое
ожидание общего числа попаданий.
Решение
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт вступайте в группу ВКсохраните контакт WhatsApp ( 79688494598) сохраните контакт Телеграм (@helptask) .
Число
попаданий при первом выстреле есть случайная величина
, которая может принимать
только два значения:1 –
попадание с вероятностью
0 –
промах с вероятностью
Математическое
ожидание числа попаданий при первом выстреле:
Аналогично
находим математические ожидания числа попаданий при втором и третьем выстрелах:
Общее
число попаданий есть также случайная величина, состоящая из суммы попаданий в
каждом из трех выстрелов:
Искомое
математическое ожидание:
Ответ:
Пример 4
Найти
математическое ожидание суммы числа очков, которые могут выпасть при бросании
двух игральных костей.
Решение
Обозначим
число очков, которое может выпасть на первой кости, через
, и на второй – через
.
Возможные
значения этих величин одинаковы и равны: 1,2,3,4,5 и 6.
При этом
вероятность каждого из этих значений равна 1/6.
Математическое
ожидание числа очков, выпавших на первой кости:
Аналогично
математическое ожидание числа очков, выпавших на второй кости:
Искомое
математическое ожидание:
Ответ:.
Свойства математического ожидания
Свойство 1.
Математическое ожидание
константы равно этой константе:
Свойство 2.
Постоянный множитель
можно выносить за знак математического ожидания:
Свойство 3.
Математическое ожидание
суммы случайных величин равно сумме математических ожиданий слагаемых:
Свойство 4.
Математическое ожидания
произведения случайных величин:
где
–
ковариация случайных величин
и
В частности, если
и
независимы, то
И вообще, для независимых случайных величин
математическое ожидание их произведения равно произведению математических
ожиданий сомножителей:
Смежные темы решебника:






